高等数学A2 2020/5/12 第二十三次课
返回主索引
三重积分 (下)
柱面坐标下的三重积分
柱面坐标 = 极坐标 + 竖坐标
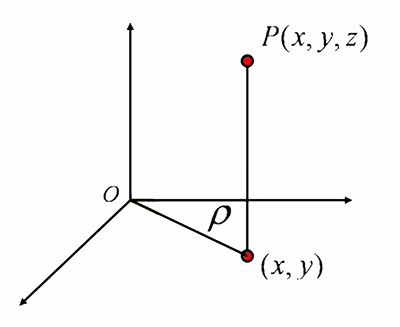
\(P(x,y,z)\to P(\rho ,\theta ,z) \;\;\;\;\;\;\;\;P(\rho ,\theta ,z)\to P(x,y,z)\)
\(\begin{cases}x=\rho cos\theta\\y=\rho sin\theta\\z=z\end{cases}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\begin{cases}\rho =\sqrt{x^2+y^2}\\\theta=arctan\frac{y}{x}\\z=z\end{cases}\)
\((0\le\rho\le\infty\;,\;\;\;0\le\theta\le 2\pi\;,\;\;\;-\infty<z<+\infty)\)
计算方法
柱面坐标的体积元素:\(dv=dxdydz=\rho d\rho d\theta dz\)
三重积分从直角坐标到柱面坐标的变化:
\(\iiint\limits_{\Omega}f(x,y,z)dxdydz=\iiint\limits_{\Omega}f(\rho cos\theta ,\rho sin\theta ,z)\rho d\rho d\theta dz\)
使用情形
当 \(\Omega\) 在 \(xOy\) 面上的投影为圆域时,用柱面坐标计算三重积分比较方便,常用于圆柱体,圆锥体等
例子
\(\Omega:0\le\theta\le 2\pi\;,\;\;\;0\le\rho\le 2\;,\;\;\;\rho\le z\le 2\)
\(f(x,y,z)=x^2+y^2=\rho ^2\)
则 \(\iiint\limits_{\Omega}f(x,y,z)=\int^{2\pi }_{0}d\theta\int^2_0d\rho\int^2_\rho\rho ^2·\rho dz\)
球面坐标下的三重积分
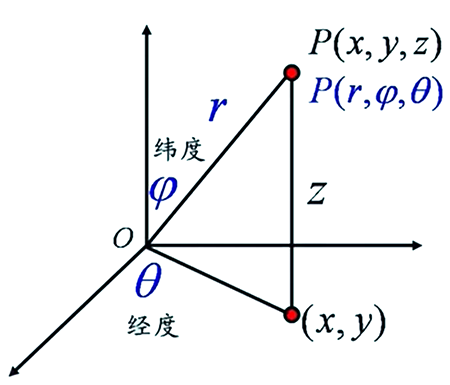
\(P(x,y,z)\to P(r ,\varphi ,\theta ) \;\;\;\;\;\;\;\;P(r ,\varphi ,\theta )\to P(x,y,z)\)
\(\begin{cases}x=rsin\varphi cos\theta\\y=rsin\varphi sin\theta\\z=rcos\varphi\end{cases}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\begin{cases}r=\sqrt{x^2+y^2+z^2}\\\varphi=arctan\frac{y}{x}\\\theta=arccos\frac{z}{r}\end{cases}\)
\((0\le r<+\infty\;,\;\;\;0\le\theta< 2\pi\;,\;\;\;0\le \varphi\le\pi)\)
计算方法
球面坐标的体积元素:\(dv=dxdydz=r^2sin\varphi drd\varphi d\theta\)
三重积分从直角坐标到球面坐标的变化:
\(\iiint\limits_{\Omega}f(x,y,z)dxdydz=\iiint\limits_{\Omega}f(rsin\varphi cos\theta ,rsin\varphi sin\theta, rcos\varphi)\)
使用情形
有球体或半球体出现时
积分区域的轮换对称性
设 \(\Omega\) 关于 \(x,y,z\) 具有轮换对称性,即若 \((x,y,z)∈\Omega\),
则将 \(x,y,z\) 任意互换后的点也属于 \(\Omega\),则被积函数中的自变量可以任意呼唤而不会改变积分值,
即:\(\iiint\limits_{\Omega}f(x,y,z)dv=\iiint\limits_{\Omega}f(y,x,z)dv=\iiint\limits_{\Omega}f(z,x,y)dv\)
\(\iiint\limits_{\Omega}f(x)dv=\iiint\limits_{\Omega}f(y)dv=\iiint\limits_{\Omega}f(z)dv\)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号