高等数学A2 2020/5/9 第二十二次课
返回主索引
三重积分（上）
定义
三重积分的一般表示如下：
\(I=\iiint\limits_{\Omega}f(x,y,z)dV\)
它最佳的理解方式是 —— 空间物体的质量，即空间物体占据空间区域 \(\Omega\)，
在点 \((x,y,z)\) 处的体密度为 \(f(x,y,z)\) ，
整个空间物体的总质量就是将 \(f(x,y,z)\) 累积遍整个空间区域 \(\Omega\) 。
三重积分的计算
利用直角坐标（先一后二法）
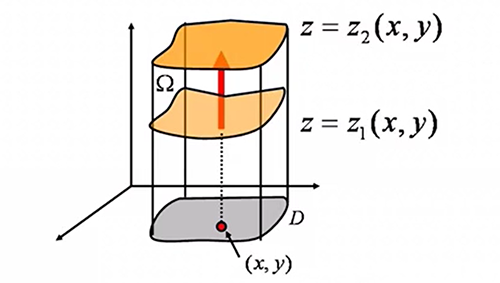
\(\iiint\limits_{\Omega}f(x,y,z)dv=\iint\limits_{D}[\int^{z_2(x,y)}_{z_1(x,y)}f(x,y,z)dz]dxdy\)
\(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\,=\iint\limits_{D}dxdy\int^{z_2(x,y)}_{z_1(x,y)}f(x,y,z)dz\)
于是转化成计算 一重积分 + 二重积分 的问题
利用平行切面（先二后一法）
原理：对平行切面的质量求积分得到空间物体的质量
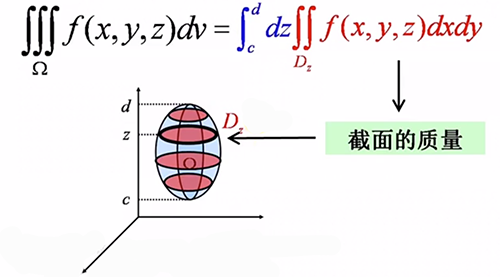
\(\iiint\limits_{\Omega}f(x,y,z)dv=\int^d_cdz\iint\limits_{D_z}f(x,y,z)dxdy\)
于是转化成计算 二重积分 + 一重积分 的问题
