动态规划:P2585[ZJOI2006]三色二叉树
P2585[ZJOI2006]三色二叉树
题目:
思路分析:
可以借鉴动态规划:P1352没有上司的舞会 - 朱朱成 - 博客园 (cnblogs.com),建立一个二维的dp 第二维01代表有没有去,有没有染成绿色的。对于一个结点来说,以这个结点为根的子树,染成绿色的数目,因为是二叉树,所以一个结点只会连两个结点,所以不染成绿色的就等于max(左子节点染成绿色,的左子树绿色数目总和,右子节点不染成绿色,的右子树绿色数目总和),因为不染成绿色,左右子节点必有一个染成绿色,取最优就行,因为是三种颜色,所以不可能父节点不成绿色,两个子节点也不是绿色,可以根据抽屉原理得知。然后其他的计算其实跟其他两种颜色没关系了,就考虑染不染成绿色。然后我们再计算这个点染成绿色,就等于左子节点不染成绿色,的左子树绿色数目总和+右子节点不染成绿色,的右子树绿色数目总和+1。注意+1,就是父节点刚染成绿色的1。然后利用DFS,按照这个思路树形DP即可。因为题目是求最多和最少的,所以构建两个DP数组,max改成min即可。
关键DP代码:

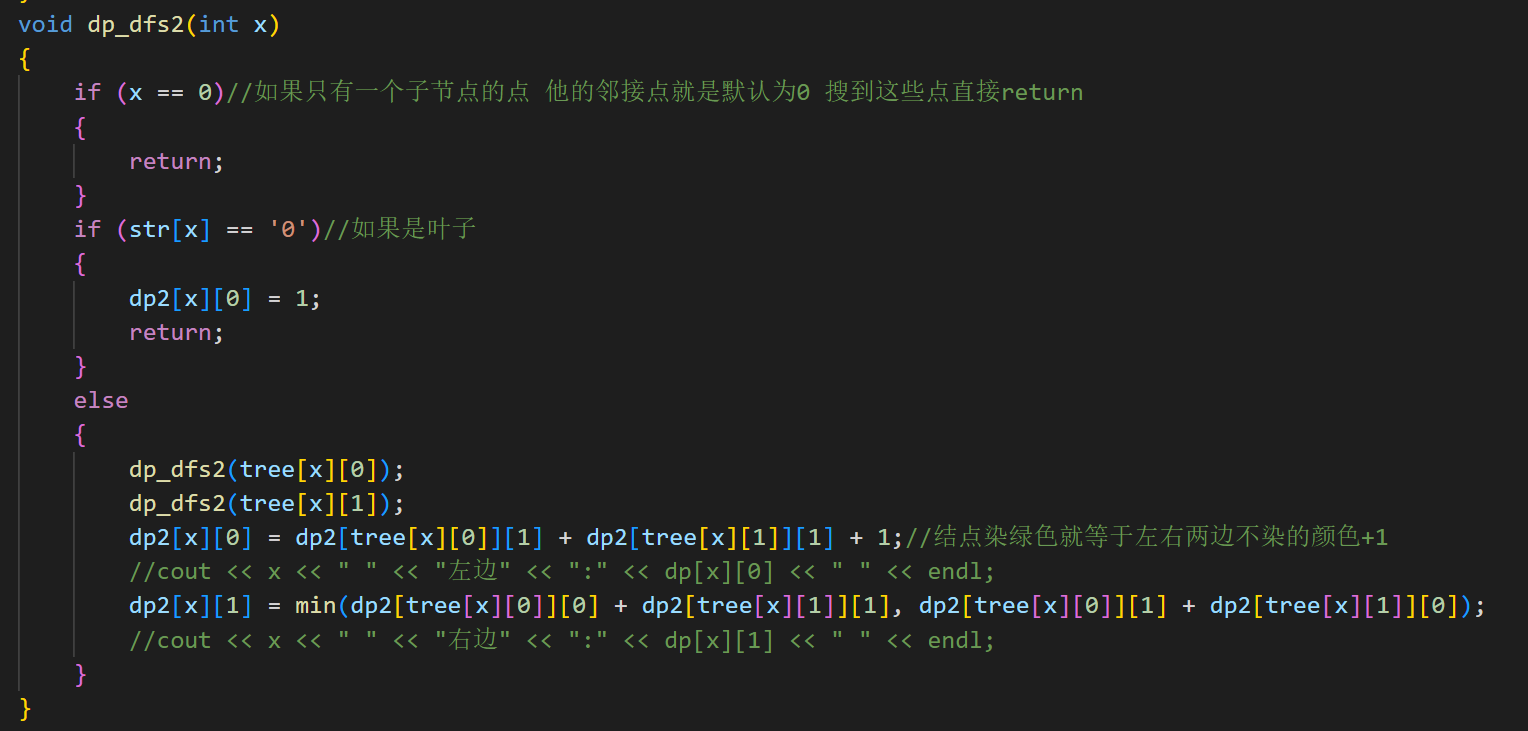
AC完整代码:
1 #include <cstring> 2 #include <cmath> 3 #include <cstdio> 4 #include<iostream> 5 using namespace std; 6 const int maxn = 5 * 1e5 + 5; 7 //设tree[i][0] 为第i个节点的左节点编号 8 //设tree[i][1] 为第i个节点的右节点编号 9 //dp[i][0]为第i个节点 为根 并且这个结点涂绿色 的子树 绿色最多的数量 10 //dp[i][12]为第i个节点 为根 并且这个结点不涂绿色 的子树 绿色最多的数量 11 int dp1[maxn][2];//一个求max 一个求min 12 int dp2[maxn][2]; 13 int tree[maxn][2]; 14 int cnt; 15 string str; 16 void dfs(int root) 17 { 18 cnt++;//表示访问了x个点 19 if (str[root] == '0') 20 return; 21 if (str[root] == '1') 22 { 23 tree[root][0] = root + 1;//如果有只有一个子节点 一定是左边结点 并且就是下一个root+1 24 dfs(root + 1);//搜索下一个点 25 } 26 else if (str[root] == '2') 27 { 28 tree[root][0] = root + 1; 29 dfs(root + 1); 30 tree[root][1] = cnt + 1;//右结点就是访问的点数+1 31 dfs(cnt + 1); 32 } 33 } 34 35 void dp_dfs1(int x) 36 { 37 if (x == 0)//如果只有一个子节点的点 他的邻接点就是默认为0 搜到这些点直接return 38 { 39 return; 40 } 41 if (str[x] == '0')//如果是叶子 42 { 43 dp1[x][0] = 1; 44 return; 45 } 46 else 47 { 48 dp_dfs1(tree[x][0]); 49 dp_dfs1(tree[x][1]); 50 dp1[x][0] = dp1[tree[x][0]][1] + dp1[tree[x][1]][1]+1;//结点染绿色就等于左右两边不染的颜色+1 51 //cout << x << " " << "左边" << ":" << dp[x][0] << " " << endl; 52 dp1[x][1] = max(dp1[tree[x][0]][0] + dp1[tree[x][1]][1], dp1[tree[x][0]][1] + dp1[tree[x][1]][0]); 53 //cout << x << " " << "右边" << ":" << dp[x][1] << " " << endl; 54 } 55 } 56 void dp_dfs2(int x) 57 { 58 if (x == 0)//如果只有一个子节点的点 他的邻接点就是默认为0 搜到这些点直接return 59 { 60 return; 61 } 62 if (str[x] == '0')//如果是叶子 63 { 64 dp2[x][0] = 1; 65 return; 66 } 67 else 68 { 69 dp_dfs2(tree[x][0]); 70 dp_dfs2(tree[x][1]); 71 dp2[x][0] = dp2[tree[x][0]][1] + dp2[tree[x][1]][1] + 1;//结点染绿色就等于左右两边不染的颜色+1 72 //cout << x << " " << "左边" << ":" << dp[x][0] << " " << endl; 73 dp2[x][1] = min(dp2[tree[x][0]][0] + dp2[tree[x][1]][1], dp2[tree[x][0]][1] + dp2[tree[x][1]][0]); 74 //cout << x << " " << "右边" << ":" << dp[x][1] << " " << endl; 75 } 76 } 77 int main() 78 { 79 cin >> str; 80 for (int i = str.length(); i >= 1; --i) 81 { 82 str[i] = str[i - 1]; 83 } 84 dfs(1); 85 dp_dfs1(1); 86 dp_dfs2(1); 87 cout << max(dp1[1][0], dp1[1][1]); 88 cout << " "; 89 cout << min(dp2[1][0], dp2[1][1]); 90 return 0; 91 92 }