动态规划：P2014[CTSC1997] 选课 分组背包 树形DP 分组背包

P2014[CTSC1997] 选课 

题目传送门：P2014 [CTSC1997] 选课 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

题目：

 

 思路：

这题思路跟我的动态规划：P2015二叉苹果树 树形DP 分组背包 - 朱朱成 - 博客园 (cnblogs.com) 思路一模一样，唯一有区别的这题是点权，不再是边权，所以我们计算每个结点连的结点数，要把每个结点数sum[i]初始化为1，然后sum[结点]是+=sum[邻接点]，其他都一样。

关键DP代码：

 

 

 

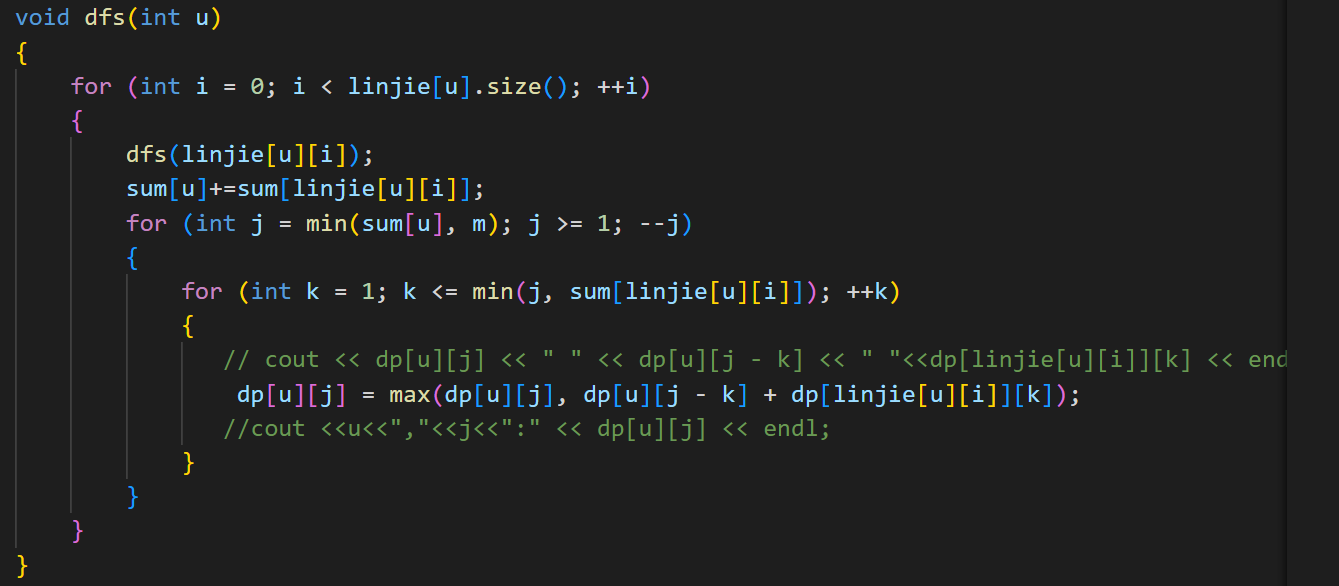
完整代码：

#include<iostream>
#include<algorithm>
#include<vector>
#include<cstring>
using namespace std;
const int maxn = 305;
vector<int>linjie[maxn];
int val[maxn];
int n, m, a, b;
int dp[maxn][maxn];
int sum[maxn];
int xuefen[maxn];
void dfs(int u)
{
    for (int i = 0; i < linjie[u].size(); ++i)
    {
        dfs(linjie[u][i]);
        sum[u]+=sum[linjie[u][i]];
        for (int j = min(sum[u], m); j >= 1; --j)
        {
            for (int k = 1; k <= min(j, sum[linjie[u][i]]); ++k)
            {
               // cout << dp[u][j] << " " << dp[u][j - k] << " "<<dp[linjie[u][i]][k] << endl;
                dp[u][j] = max(dp[u][j], dp[u][j - k] + dp[linjie[u][i]][k]);
               //cout <<u<<","<<j<<":" << dp[u][j] << endl;
            }
        }
    }
}
int main()
{
    cin >> n >> m;
    memset(dp, -0x3f, sizeof(dp));
    dp[0][0] = 0;
    for (int i = 1; i <= n; ++i)//构建邻接关系
    {
        cin >> a >> b;
        linjie[a].push_back(i);
        val[i] = b;
        dp[i][1] = b;
    }
    for (int i = 1; i <= n; ++i)
    {
        sum[i] = 1;//初始化
    }
   // countsum(0);
    dfs(0);
    cout << dp[0][m];
    return 0;
}

/*
4 2
0 1
0 2
1 3
1 4
*/