动态规划：P2015二叉苹果树 树形DP 分组背包

P2015二叉苹果树

题目传送门：P2015 二叉苹果树 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

题目:

 

 思路分析：

　　观察题目可以看出，这是一个有边权的二叉树。找到一颗子树，使边的个数满足题目限定的数量，并且边权和最大。显然是树形DP 要用分组背包的思路，构造二维DP数组，dp[i][j]代表的时候以i为根节点，连接j个枝条的时候，的总权值和。但是注意分组背包的时候，对于每一结点，利用分组背包DP模板时，要考虑取值范围，j的范围是min(m,size[本结点])，size数组的意思就是从上往下搜，这个结点向下连的总枝条数，这里有个技巧，不用再一个函数来计算连接的枝条数，直接在dfs里计算，在for循环遍历邻接点时，dfs邻接点后，size(根节点)+=size(邻接点)+1,+1就是+根节点和邻接点的枝条，因为dfs邻接点在计算size之前，所以size（邻接点）一定是算出来的，考虑叶子结点，叶子结点不进行for循环，枝条数为0，因为叶子结点向下连的枝条数为0，显然这样做是可以的。

　　关键DP代码：

 

 

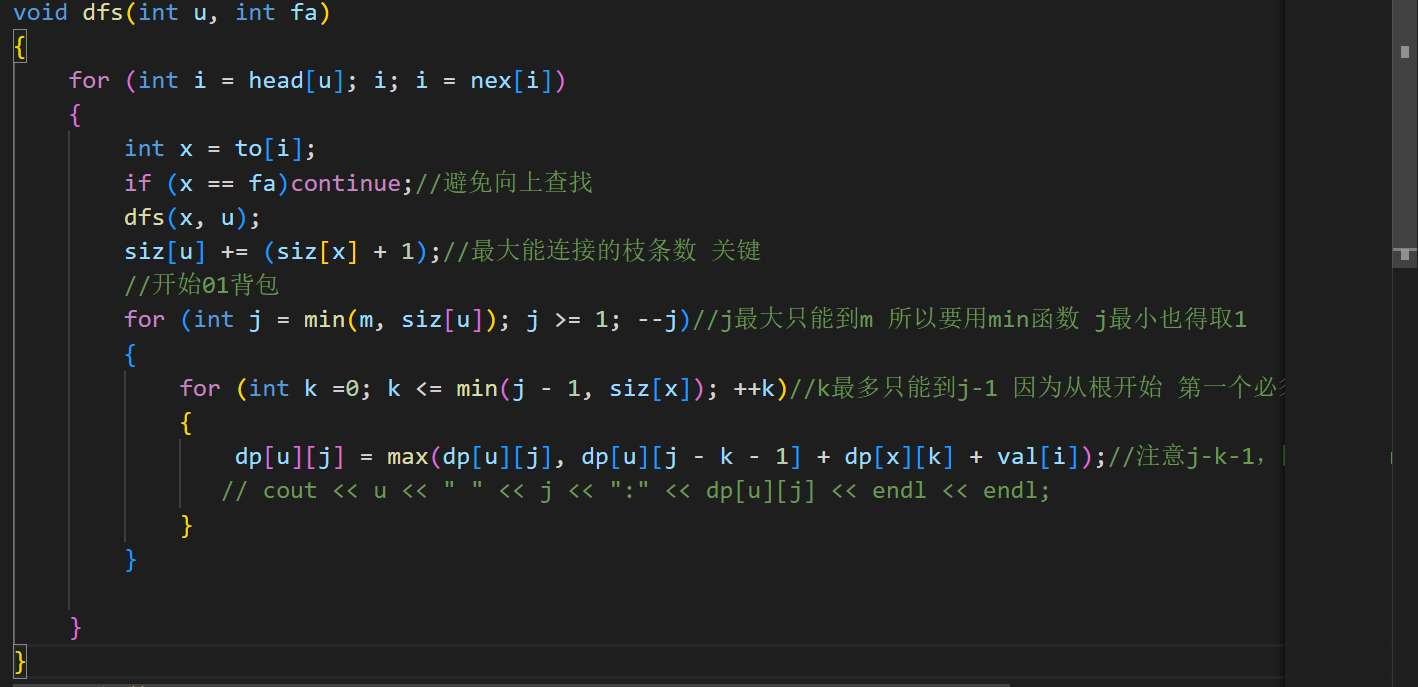
 总代码：

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
const int maxn = 3 * 1e2 + 5;
const int inf = 0x7fffffff;
int n, m;
int dp[maxn][maxn];//表示以i为起点 留j个枝条 的权值和
int head[maxn], val[2 * maxn], to[2 * maxn], nex[2 * maxn], index;
int siz[maxn];
void add(int a, int b, int c)
{
    index++;
    to[index] = b;
    nex[index] = head[a];
    head[a] = index;
    val[index] = c;
}
void dfs(int u, int fa)
{
    for (int i = head[u]; i; i = nex[i])
    {
        int x = to[i];
        if (x == fa)continue;//避免向上查找
        dfs(x, u);
        siz[u] += (siz[x] + 1);//最大能连接的枝条数 关键
        //开始01背包
        for (int j = min(m, siz[u]); j >= 1; --j)//j最大只能到m 所以要用min函数 j最小也得取1
        {
            for (int k =0; k <= min(j - 1, siz[x]); ++k)//k最多只能到j-1 因为从根开始 第一个必须要 也就是u结点必须选 
            {
                dp[u][j] = max(dp[u][j], dp[u][j - k - 1] + dp[x][k] + val[i]);//注意j-k-1，因为连接u 和x还有一个树枝
               // cout << u << " " << j << ":" << dp[u][j] << endl << endl;
            }
        }

    }
}
int main()
{
    cin >> n >> m;
    for (int i = 1; i < n; ++i)
    {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
        add(b, a, c);
    }
    dfs(1, -1);
    cout << dp[1][m];
    return 0;
}

 

通过：