动态规划：P1040[NOIP2003 提高组] 加分二叉树 树形DP

P1040[NOIP2003 提高组] 加分二叉树

题目传送门：P1040 [NOIP2003 提高组] 加分二叉树 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

题目：

 

思路：

　　题目给的是中序遍历，所以一定是根左右，在序列中，对于每一个结点，他左边的数字可能就是他的左结点，或者左子树为空，右边的数字可能就是他的右结点，或者右子树为空，右边的数字跟他没关系。所以我们可以先看每一个点，对于每一个点来说，以他自己为一棵树，左子树右子树均为空的加分就是他的点权，可以通过题目的加分计算方法得知。我们先构建dp[i][j] 数组 dpi j 就代表以i为树的最左边的点，j为树的最右边的点构造树，因为是中序遍历 左根右。由刚刚推导的一个点为树的情况，dp[i][i]就都等于点权，所以初始化的时候，不需要再构建点权数组，直接初始化在dp[i][i],然后我们寻求状态转移，对于下一个状态，也就是树里面只有两个点的情况，我们的思路就是从树只有一个点推到树序列的总长度，有点吧这一题转化为区间DP了，因为他给的中序序列构造出来的树是任意的，无法用构造树以后去做。那么对于区间长度为2的dp[l][r]，先初始化为dp[l+1][r]+dp[l][l];//默认左子树为空，然后进行切割，也就是对于这个区间，在中间选取一个结点做根，因为是中序遍历，根左右，但是对于长度为2的点，无法切割，选根其实只能从长度为3的开始，因为根左右，主要是长度为2的点没必要切割，他默认左树为空和右子树为空，和初始化的值是一样的，切割也就这两种情况，没有必要，然后就从2一直推到n，但是要求前序遍历，根左右，每一次切割找到更好地根就记录root[i][j]=k k就是最好的根，我们构建这个root就是存区间为i j 时最优的根k，然后递归寻找路径，或者前序序列。构造一个find函数，每次传入区间的l and r，输出根root [l][r]，因为是前序序列，所以再find中再递归调用find查找左区间和有区间，find l k-1,and find k+1 r  注意递归返回条件 当l==r 时，就输出l 因为是以自己为根 这就是叶子结点，l>r 就直接return，边界条件。

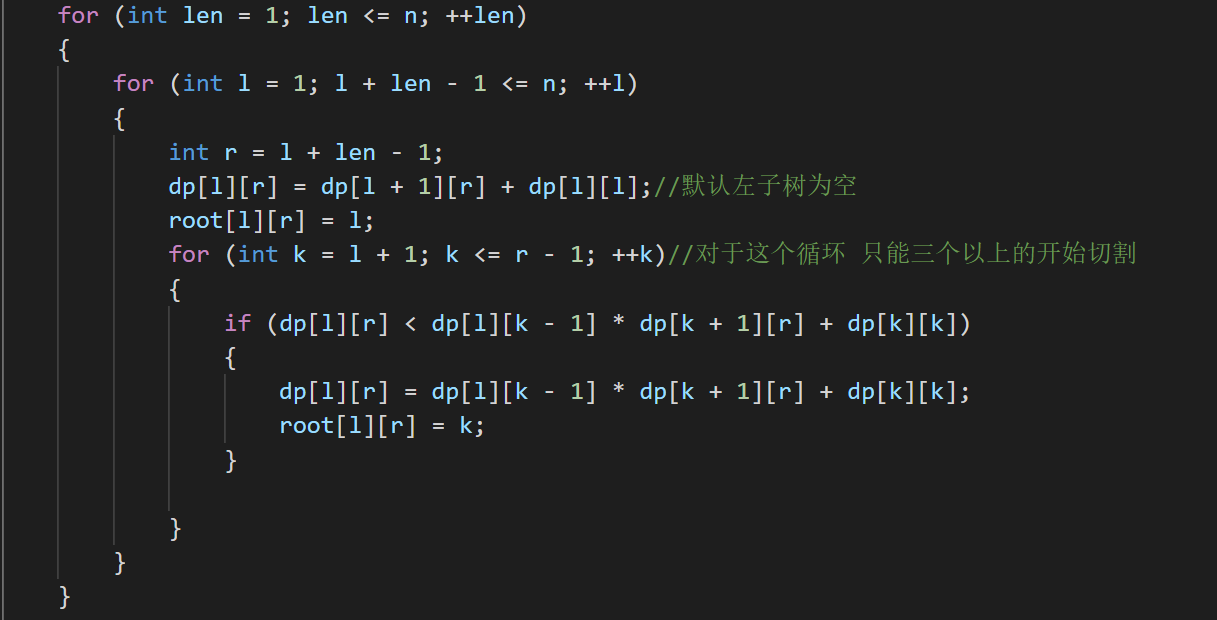
　　关键DP代码：

 

 

 

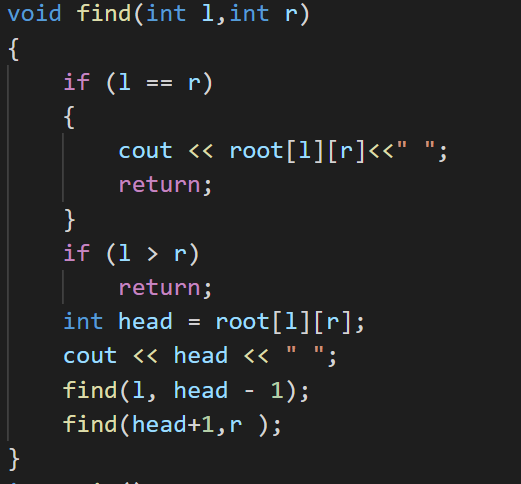
find函数：

 

 

完整AC代码：

#include<iostream>
using namespace std;
typedef long long ll;
const int maxn = 50;
ll dp[maxn][maxn];
int root[maxn][maxn];
int n;
void find(int l,int r)
{
    if (l == r)
    {
        cout << root[l][r]<<" ";
        return;
    }
    if (l > r)
        return;
    int head = root[l][r];
    cout << head << " ";
    find(l, head - 1);
    find(head+1,r );
}
int main()
{
    cin >> n;
    for (int i = 1; i <= n; ++i)
    {
        cin >> dp[i][i];
        root[i][i] = i;
        // dp[i][i-1]=1;
    }
    for (int len = 1; len <= n; ++len)
    {
        for (int l = 1; l + len - 1 <= n; ++l)
        {
            int r = l + len - 1;
            dp[l][r] = dp[l + 1][r] + dp[l][l];//默认左子树为空
            root[l][r] = l;
            for (int k = l + 1; k <= r - 1; ++k)//对于这个循环 只能三个以上的开始切割
            {
                if (dp[l][r] < dp[l][k - 1] * dp[k + 1][r] + dp[k][k])
                {
                    dp[l][r] = dp[l][k - 1] * dp[k + 1][r] + dp[k][k];
                    root[l][r] = k;
                }
               
            }
        }
    }
    cout << dp[1][n]<<endl;
    find(1, n);
    return 0;
}