动态规划：P1273有线电视网 树形DP 有依赖的背包+分组背包
思路：这题其实就是 有依赖的背包+分组背包
意思就是一棵树，边权就是花费，点权就是赚的费用，求包括以根结点为根的子树，使得他连接的用户最多。所以我们构建DP[I][J]二维DP，显然这是一个有依赖的分组背包问题，I就代表以第I个结点为根，J就代表连着j个用户，DP的意思就是他的净利润，那么只要DP[1][j]j从大遍历到小，只要让DP值 ≥ 0 就取最大的那个J，就是最多的连接用户数。因为题目说不亏本就行，所以净利润 ≥ 0即可。所以这边就有一个注意点，因为要求的是≥0的数据，所以我们不能初始化DP数组为0，会影响最后的ans，所以初始化DP数组为-inf。这里要求出每个结点最多能连的用户数，避免多算，自己写一个makesum函数，求出每个结点对应下面的叶子节点数，这样便于在DFS时，分组背包，得出j的上界。点权就直接初始化在DP[叶子结点][1];我们分组背包的转移方程就是DP[I][J]=MAX(DP[I][J],DP[邻接点][k]+DP[I][J-K]-边权[邻接点]) （由于每一个结点只有一个父节点，所以我们定义这个边权时，就直接按子节点的编号定义一维数组，可以做到唯一性。），状态转移方程的意思就是，对于一个父节点，他如果连这个子节点，就需要减去边权也就是花费，连这个子节点就是分组背包的问题，要写出二维数组，分组背包的模板具体可以看我动态规划：有依赖的背包 树形DP+分组背包 - 朱朱成 - 博客园 (cnblogs.com)里面的题解。这边还有一个注意点就是，我们要初始化DP[i][1](不是叶子节点的时候) dp[i][1]是从 dp[i][0]+dp[邻接的叶子][1]-边权得来的，但是dp[i][0]被初始化为-inf 了 是不可以的，所以我们一定要把除了叶子结点外的dp[i][0]全部初始化为0，这就是两个边界条件的注意点。
关键DP代码：
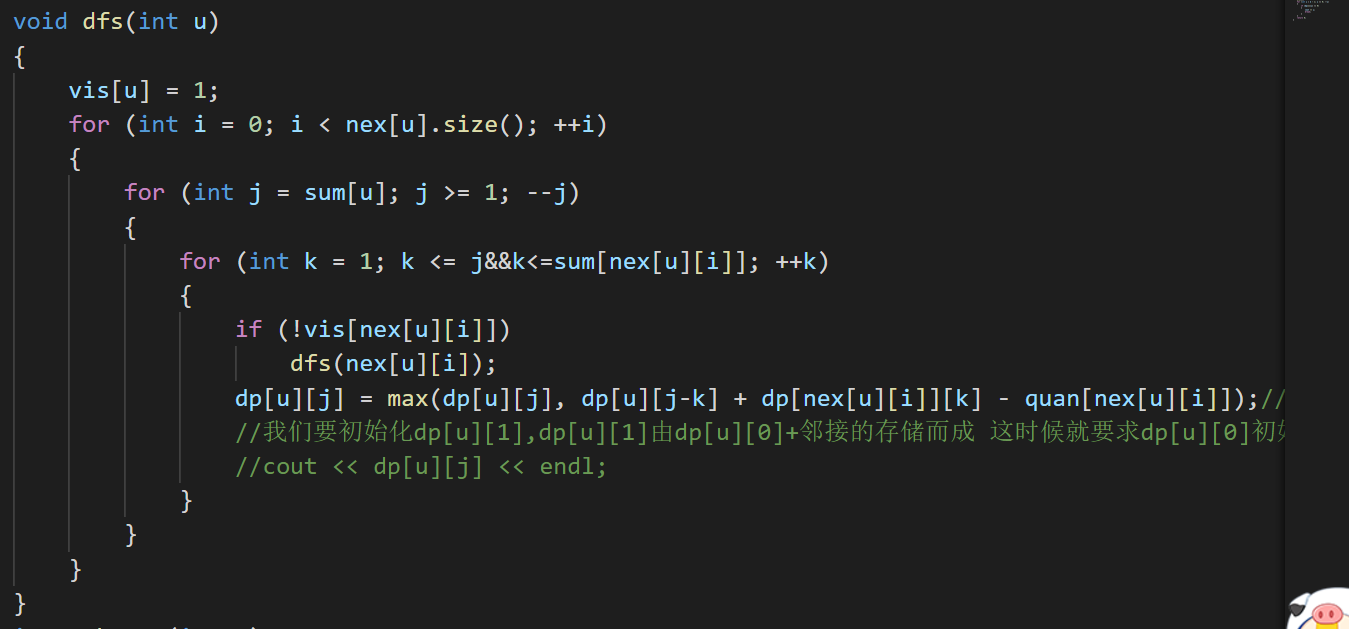
求每一个结点连的叶子和makesum函数：
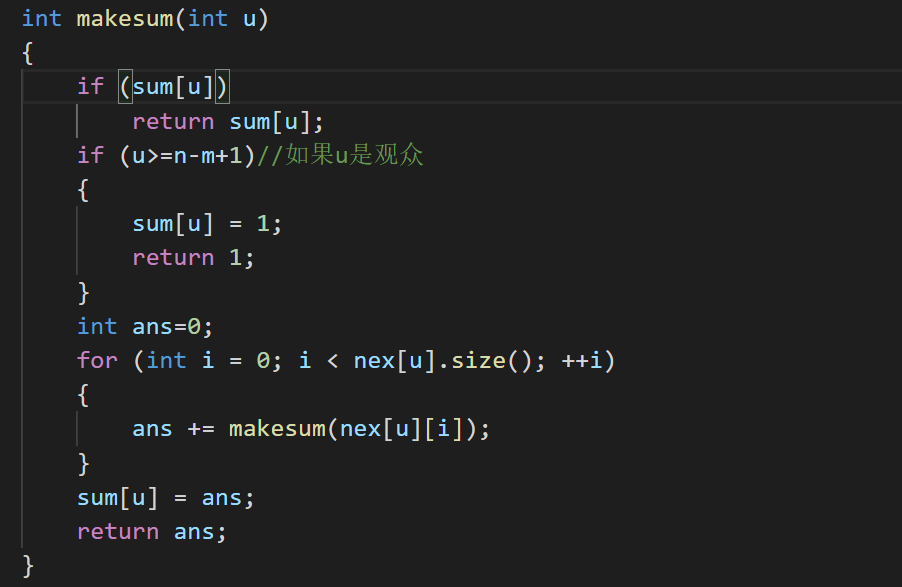
完整代码：
1 #include<iostream> 2 #include<algorithm> 3 #include<vector> 4 #include<cstring> 5 using namespace std; 6 const int maxn = 3005; 7 vector<int>nex[maxn]; 8 int quan[maxn]; 9 int sum[maxn]; 10 int dp[maxn][maxn];//记录以i为根 连接j个用户的利润 11 bool vis[maxn]; 12 int n, m, k,a,b; 13 void dfs(int u) 14 { 15 vis[u] = 1; 16 for (int i = 0; i < nex[u].size(); ++i) 17 { 18 for (int j = sum[u]; j >= 1; --j) 19 { 20 for (int k = 1; k <= j&&k<=sum[nex[u][i]]; ++k) 21 { 22 if (!vis[nex[u][i]]) 23 dfs(nex[u][i]); 24 dp[u][j] = max(dp[u][j], dp[u][j-k] + dp[nex[u][i]][k] - quan[nex[u][i]]);//当j-k=0 时候 25 //我们要初始化dp[u][1],dp[u][1]由dp[u][0]+邻接的存储而成 这时候就要求dp[u][0]初始化为0 26 //cout << dp[u][j] << endl; 27 } 28 } 29 } 30 } 31 int makesum(int u) 32 { 33 if (sum[u]) 34 return sum[u]; 35 if (u>=n-m+1)//如果u是观众 36 { 37 sum[u] = 1; 38 return 1; 39 } 40 int ans=0; 41 for (int i = 0; i < nex[u].size(); ++i) 42 { 43 ans += makesum(nex[u][i]); 44 } 45 sum[u] = ans; 46 return ans; 47 } 48 int main() 49 { 50 cin >> n >> m; 51 memset(dp, -0x3f, sizeof(dp));//因为是main外定义 初始值都是0 但是最后利润为0也可以 52 //判断是否是ans就是看dp>=0，但是初始值是0，会影响正确ans的judge 所以要初始化为-inf一下 53 for (int i = 1; i <= n - m; ++i) 54 { 55 cin >> k; 56 for (int j = 1; j <= k; ++j) 57 { 58 cin >> a >> b; 59 nex[i].push_back(a);//邻接关系 60 quan[a] = b;//money 61 } 62 dp[i][0] = 0;//这个必须初始化 不然算不出来转播台结点只有一个观众的初值 63 } 64 for (int i = n-m+1; i <= n; ++i) 65 { 66 cin >> dp[i][1]; 67 vis[i] = 1; 68 // cout << dp[i][1] << endl; 69 } 70 makesum(1); 71 dfs(1); 72 for (int j = m - 1; j >= 0; --j) 73 { 74 if (dp[1][j] >= 0) 75 { 76 cout << j; 77 break; 78 } 79 } 80 return 0; 81 }
通过图：
