动态规划:有依赖的背包 树形DP+分组背包
有依赖的背包
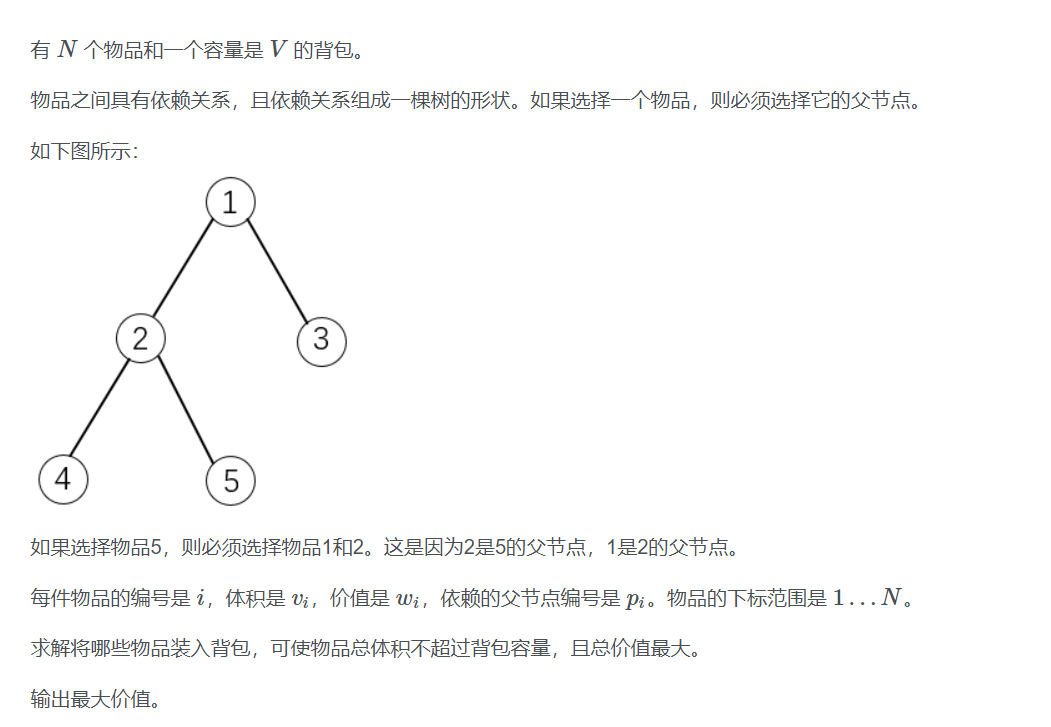

思路:
先构建DP二维数组 ,DP[I][J] 代表以i为起点装体积为J的物品能获得的最大价值。我们先从根开始搜索,设价值数组为W[] 体积数组为 V[] ,搜索到的结点为U, 对于U这个结点来说,我们先初始化,DP[U][i],i从V[U]到MAXV,因为要装入U这个东西,背包的容量起码要有V[U],最大就只能到题目限制的MAXV,我们初始化所有的DP[U][I]都为V[U],因为要U这个东西,我们就装入U的value。要开始01背包,必须知道本结点U所有邻接的结点的DP值,所以我们来一个for循环遍历所有邻接点,并且继续DFS这些点,每次DFS后开始01背包,01背包两重循环,外层为体积,肯定是MAXV到V[U],注意01背包是从大到小,做到无后效性。但是这个是分组背包,就是对于这个体积的背包,他的邻接点,我可以有多个选择,比如设邻接点为X,外层循环i:MAXV->V[U], 那么DP[U][i]=max(DP[U][i-j]+DP[X][j]) ,j是什么意思呢,我们应该加一个内层循环,j就是从0到i-V[U],就是邻接的这个小背包能提供的体积和价值的几种可能,相当于有多组背包。 注意j的取值范围,内层背包最少提供0体积,最多提供i-V[u],因为j-i>=V[U],起码得让这个背包放得下这层的V[U]。这是分组背包一个很经典的模型。
关键DP代码:

完整代码:
1 #include<iostream> 2 #include<algorithm> 3 #include<vector> 4 using namespace std; 5 int n, m, root; 6 int dp[110][110];//表示选择以u为子树 在体积和不超过容量j时获得的最大价值 7 vector<int>a[110];//动态数组存储邻接点 8 int v[110], w[110]; 9 void dfs(int u) 10 { 11 for (int i = v[u]; i <= m; ++i) 12 dp[u][i] = w[u];//若选了u 体积不能小于v[u]; 13 for (int i = 0; i < a[u].size(); ++i) 14 { 15 int s = a[u][i];//a[u] u所邻接的物品 16 dfs(s); 17 for (int j = m; j >= v[u]; j--)//体积 18 for (int k = 0; k <= j - v[u]; k++)//决策 19 { 20 dp[u][j] = max(dp[u][j], dp[u][j - k] + dp[s][k]); 21 } 22 } 23 } 24 int main() 25 { 26 cin >> n >> m; 27 for (int i = 1; i <= n; ++i) 28 { 29 int p; 30 cin >> v[i] >> w[i] >> p; 31 if (p == -1) 32 root = i;//存储根的值,到时候dfs从根开始搜 33 else 34 { 35 //把p的邻接点i存入数组a的p层 36 a[p].push_back(i); 37 } 38 } 39 dfs(root); 40 cout << dp[root][m]; 41 return 0; 42 }
完美通过:




