动态规划:积蓄程度( 树形DP+ 换根 +二次扫描)
积蓄程度
题目:
有一个树形的水系,由 N-1 条河道和 N 个交叉点组成。
我们可以把交叉点看作树中的节点,编号为 1~N,河道则看作树中的无向边。
每条河道都有一个容量,连接 x 与 y 的河道的容量记为 c(x,y)。
河道中单位时间流过的水量不能超过河道的容量。
有一个节点是整个水系的发源地,可以源源不断地流出水,我们称之为源点。
除了源点之外,树中所有度数为 1 的节点都是入海口,可以吸收无限多的水,我们称之为汇点。
也就是说,水系中的水从源点出发,沿着每条河道,最终流向各个汇点。
在整个水系稳定时,每条河道中的水都以单位时间固定的水量流向固定的方向。
除源点和汇点之外,其余各点不贮存水,也就是流入该点的河道水量之和等于从该点流出的河道水量之和。
整个水系的流量就定义为源点单位时间发出的水量。
在流量不超过河道容量的前提下,求哪个点作为源点时,整个水系的流量最大,输出这个最大值。
输入格式
输入第一行包含整数T,表示共有T组测试数据。
每组测试数据,第一行包含整数N。
接下来N-1行,每行包含三个整数x,y,z,表示x,y之间存在河道,且河道容量为z。
节点编号从1开始。
输出格式
每组数据输出一个结果,每个结果占一行。
数据范围
N≤2∗1e5
思路:任选一个结点为根,算出每个结点的全流量。那么全流量要怎么计算呢,对于任意一个结点,他都有向上的唯一条边(根没有想上的边)和向下的几条边,我们就需要算出这个结点的最大上流量,与最大下流量,他的和就是这个结点的全流量,我们可以模仿树的中心这一题,具体可以看我的动态规划:树的中心 树形DP - 朱朱成 - 博客园 (cnblogs.com),①:先向下递归,从下到上完善,算出每一个结点的下流量,这个点的下流量应该等于sum(邻接的边)min(子结点的向下流量,连接河道的容量),叶子结点的下流量设为inf:无穷大②再从上到下完善,算出根的全流量,慢慢推出其他的全流量,要算出全流量,就得算出结点的上流量,待完善结点的上流量等于min(向上流河道的容量,他的父亲结点的全流量减去min(父节点和这个结点这条河道的容量,这个结点的下流量)); 为什么要min(父节点和这个结点这条河道的容量,这个结点的下流量),意思就是算出父亲结点除了和带求子节点邻接的边,所有对外的流量,但是对于一个点来说,他的向下流量可以大于他的父亲结点指向他的这条河道的容量,所以算出父亲结点除了和带求子节点邻接的边,所有对外的流量,就要用全流量减去父亲节点和子节点这条河道的流量,这条流量应该就是min(子节点的下流量,河道容量),取小的那个。那么这个结点的全流量就等于下流量加上流量,每次更新ans。注意需要特判,我们这个式子不适用于出度为1的结点,也就是父亲节点只有一个子节点,对于这样的子节点,他的全流量就等于河道容量+下流量,原因就是可以把这个点直接作为顶点 ,等下可以画图举例。
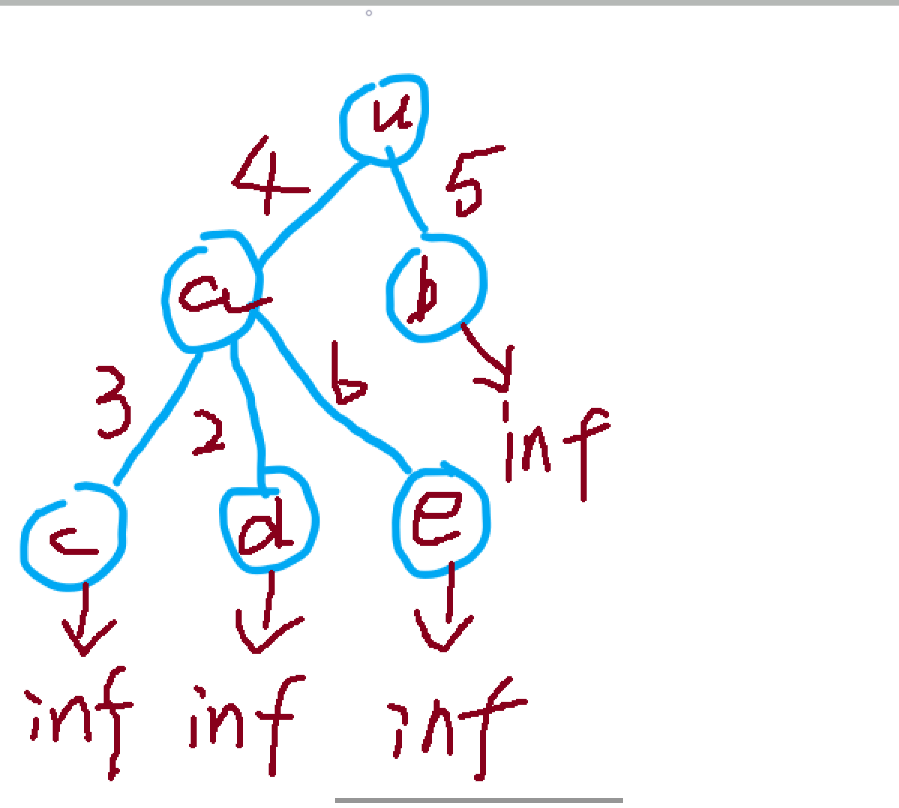
下流量: 我们画出草图,第一遍dfs算最大下流量时,对于c这个结点,他的最大下流量时inf,但是对于c的父节点a,他的最大下流量就+=min(3,inf);就是3,扫一遍后就算出a的最大下流量就是3+2+6=11,对于u的最大下流量就+=min(11,4)=4,再看第二个邻接b 所以u最大下流量还要+=min(5,inf)=5 5+4=9 所以根的最大下流量为9 但我们发现,对于每一个结点的下流量,只看下面不看上面,所以下流量很有可能大于连接这个结点的河道容量,这句话在求上流量是很重要的!。
上流量&&全流量:根节点u点的上流量不需要算,我们直接算,在外边直接计算u的全流量 就等于u点算出来的下流量。那么我们计算a点的上流量,a点的上流量就等于 取min的(他与父亲节点u的河道的容量4)与(父亲节点u除了ua这条河道 其他所有河道的流量之和),那么父亲节点u除了ua这条河道 其他所有河道的流量之和怎么算呢,就是等于父节点的全流量减去他在ua这条河道的流量,ua这条河道的流量受两个因素的制约,第一是它本身的河道容量,第二就是a的下流量之和的限制,如果河道容量大于下流量之和,那么这条河道最多只能流a的下流量之和,如果这条河道容量小于下流量之和,那么河道流量就等于河道容量,所以河道容量就等于min(下流量之和,河道容量),则(父亲节点u除了ua这条河道 其他所有河道的流量之和)就等于父节点的全流量减去河道容量。所以a点的上流量就等于min(4,9-min(4,11))=4,a点的全流量就等于下流量+上流量=11+4=15;
那么为什么要特判呢?? 如果出现度为1的情况,也就是父节点只连着一个子节点,画图举例:
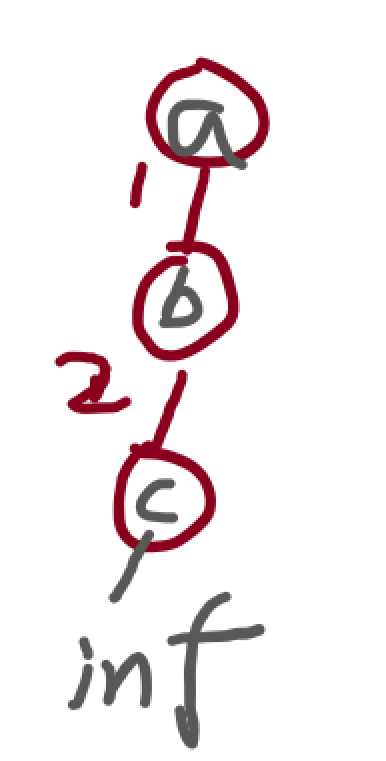
那么在考虑b点的时候用上面那个公式就会出错,我们对于b结点可以直接把b当成根节点计算,那么他的全流量就是下流量加上河道容量,也就是把它横折折一下。
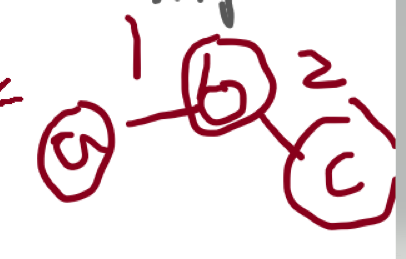
但是要计算出度,我们就要加一个数组,在存储邻接关系时,记录每一个结点的出度。或者这个结点的邻接关系为size=1,那么就用特判。
通过上面的讲解,我们就得到了关键两个dfs_d and dfs_u的代码
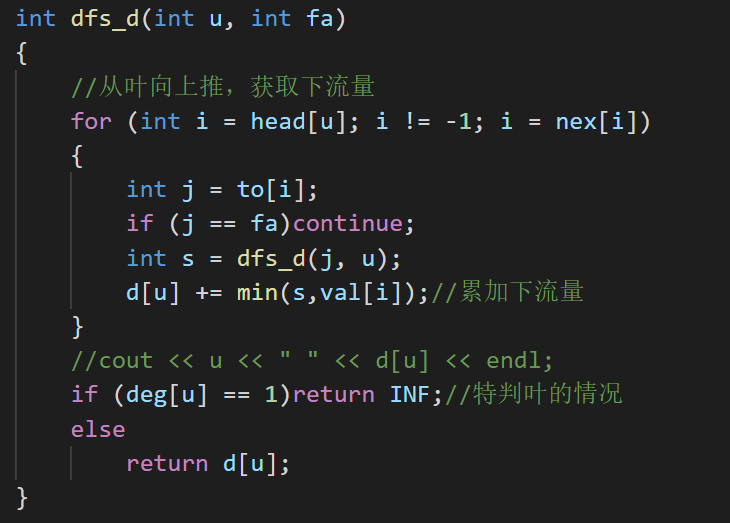

完整AC代码:
1 #include<iostream> 2 #include<algorithm> 3 using namespace std; 4 const int maxn = 2 * 1e5 + 10; 5 const int INF = 0x7fffffff; 6 int head[maxn], to[2 * maxn], nex[2 * maxn], val[2 * maxn], index;//邻接表 7 int f[maxn], d[maxn], deg[maxn];//f记录全流量 d记录下流量,deg记录入度 8 int n, a, b, c; 9 void add(int a, int b, int c) 10 { 11 index++; 12 to[index] = b; 13 nex[index] = head[a]; 14 head[a] = index; 15 val[index] = c; 16 } 17 int dfs_d(int u, int fa) 18 { 19 //从叶向上推,获取下流量 20 for (int i = head[u]; i != -1; i = nex[i]) 21 { 22 int j = to[i]; 23 if (j == fa)continue; 24 int s = dfs_d(j, u); 25 d[u] += min(s,val[i]);//累加下流量 26 } 27 //cout << u << " " << d[u] << endl; 28 if (deg[u] == 1)return INF;//特判叶的情况 29 else 30 return d[u]; 31 } 32 33 void dfs_f(int u, int fa) 34 { 35 //从根点向下推 获取j点的全流量 36 for (int i = head[u]; i != -1; i = nex[i]) 37 { 38 int j = to[i]; 39 if (j == fa)continue; 40 if (deg[u] == 1)//特判根的情况 41 { 42 f[j] = d[j] + val[i]; 43 } 44 else 45 f[j] = d[j] + min(val[i], f[u] - min(val[i], d[j])); 46 // cout << j << " " << f[j] << endl; 47 dfs_f(j, u);//深搜j点 48 } 49 } 50 int main() 51 { 52 int t; 53 cin >> t; 54 while (t--) 55 { 56 cin >> n; 57 //初始化所有数据 58 index = 0; 59 memset(head, -1, sizeof(head));//每次记得都初始化一下 60 memset(f, 0, sizeof(f)); 61 memset(d, 0, sizeof(d)); 62 memset(deg, 0, sizeof(deg)); 63 for (int i = 1; i < n; ++i) 64 { 65 cin >> a >> b >> c; 66 add(a, b, c); 67 add(b, a, c); 68 deg[a]++, deg[b]++;//出度++; 69 } 70 dfs_d(1, -1); 71 f[1] = d[1];//根只有向下的流量 72 dfs_f(1, -1); 73 int ans = 0; 74 for (int i = 1; i <= n; ++i) 75 { 76 ans = max(ans, f[i]); 77 } 78 cout << ans; 79 } 80 return 0; 81 }



