动态规划：树的中心 树形DP

树的中心

给定一棵树，树中包含 n 个结点（编号1-n)和 n−1 条无向边，每条边都有一个权值。

请你在树中找到一个点，使得该点到树中其他结点的最远距离最近。

输入格式

第一行包含整数 nn。

接下来 n−1n−1 行，每行包含三个整数 ai,bi,ci，表示点 ai和 bi之间存在一条权值为 ci 的边。

输出格式

输出一个整数，表示所求点到树中其他结点的最远距离。

数据范围：

1≤n≤10000,1≤n≤10000,
1≤ai,bi≤n
1≤ci≤1e5

 

思路：

　　对于某一个结点，找到他向下查找距离最大值d1和距离第二大值d2 ，这个代码可以借鉴 我的 树的最长 路径代码动态规划：树的最长路径 树形DP - 朱朱成 - 博客园 (cnblogs.com)的模板，

但还需要找到向上查找的最大路径，因为这个结点也是某一个结点的子节点，所以他向上查找只会有一颗子树，求出这条路径就行。这就是这题的关键代码dfs_up 实际上是自上而下完善。

向下dfs完善向下的路径实际上是自下而上完善的过程，因为只有dfs到了最底层，也就是叶子，才算得出来倒数第二个，才算得出来倒数第三个...才能算出第一个结点。dfs_up就是自上而下完善的，

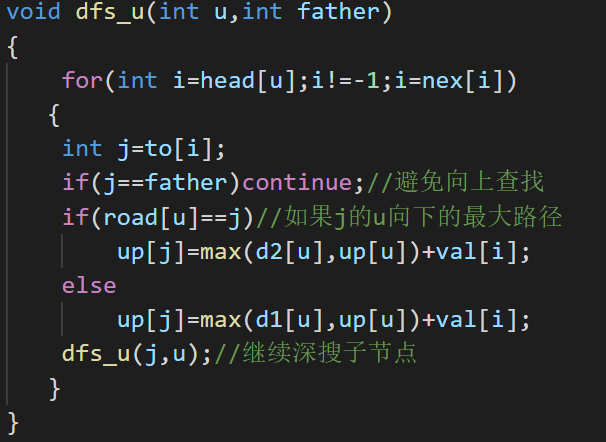
对于每一个结点，他向上查找的最大值 ，我们把这个结点称为j结点，他的根结点，也就是上一个结点，我们称为u结点，那么对于j向上查找的最大路径，存在两种情况①：若j在u的向下查找的最大路径上，

他向上查找的最大路径就是u和j的权值加上max（u向上查找的最大路径up和u向下查找的第二大路径d2）因为是自上而下完善 所以对于j的根u的向上查找的最大值up一定是已经算出来的，

②：如果j不在u向下查找的最大路径上，那么j向上查找的最大路径up就等于max（u的d1，u的up）+上j u 边的权值。

　　关键代码：

 

 

 

完整AC代码：

 1 #include<iostream>
 2 #include<algorithm>
 3 using namespace std;
 4 const int maxn = 1e4 + 5;
 5 const int inf=0x7fffffff;
 6 int head[maxn], to[2 * maxn], nex[2 * maxn], val[2 * maxn], index;//邻接表
 7 int n, a, b, c, ans;
 8 int d1[maxn],d2[maxn],up[maxn],road[maxn];
 9 //d1：向下走的最大长度 d2：向下走的次大长度 ups：向上走的最大长度 road记录向下最大长度的第一个结点
10 void add(int a, int b, int c)
11 {
12     index++;
13     val[index] = c;
14     to[index] = b;
15     nex[index] = head[a];
16     head[a] = index;
17 }
18 int dfs_d(int u,int father)
19 {
20    d1[u]=0;
21    d2[u]=0;
22    for(int i=head[u];i!=-1;i=nex[i])
23    {
24        int j=to[i];
25        if(j==father)continue;//避免向上查找
26        int d=dfs_d(j,u)+val[i];//从u经j点向下走的最大路径
27        if(d>=d1[u])d2[u]=d1[u],d1[u]=d,road[u]=j;
28        else if(d>d2[u])d2[u]=d;
29    }
30    return d1[u];
31 
32 }
33 void dfs_u(int u,int father)
34 {
35     for(int i=head[u];i!=-1;i=nex[i])
36    {
37     int j=to[i];
38     if(j==father)continue;//避免向上查找
39     if(road[u]==j)//如果j的u向下的最大路径
40         up[j]=max(d2[u],up[u])+val[i];
41     else
42         up[j]=max(d1[u],up[u])+val[i];
43     dfs_u(j,u);//继续深搜子节点
44    }
45 }
46 int main()
47 {
48     memset(head, -1, sizeof(head));//初始化邻接表为-1
49     cin >> n;
50     for (int i = 1; i < n; ++i)
51     {
52         cin >> a >> b >> c;
53         add(a, b, c);
54         add(b, a, c);
55     }
56     dfs_d(1,-1);//father先初始化为-1
57     dfs_u(1,-1);
58     int res=inf;
59     for(int i=1;i<=n;++i)
60     {
61         res=min(res,max(up[i],d1[i]));
62     }
63     cout << res;
64     return 0;
65 }

 

posted @ 2022-04-27 11:39  朱朱成  阅读(43)  评论(0)  编辑  收藏  举报