动态规划:树的重心 树形DP
树的重心
【题目】
给定一棵树,树中包括n个结点(编号1-n),和n-1条无向边。
请你找到树的重心,并输出将重心删除后,各个联通块中 结点数的最大值。
重心:是指树中的一个结点,将这个点删除后,剩余各个联通块中 结点数 的最大值 最小 那么这个点就被称为树的重心。
1<=n<=1e5
【思路】:
先构建一棵树,从某一个结点出发,求出这个结点联通块中最大的子树,我们可以画图分析
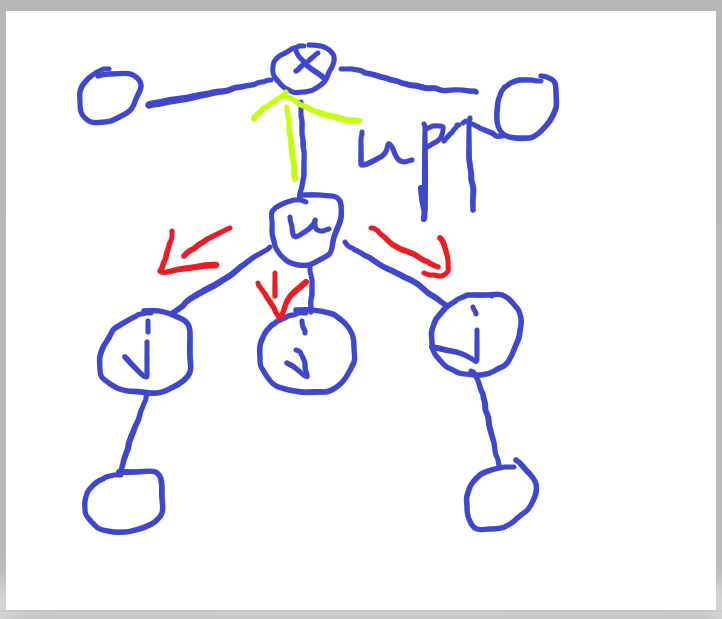
对于一个结点u 我们要求他联通块的最大size。可以从u点往下搜,设三个子树为a b c 那么最大联通块就是max(a,b,c);但这其实考虑是不够的,我们还要考虑u上面连得子树,因为一个u结点肯定也只是从上面搜下来的,所以u结点上面只会有一棵树。上面树的size其实就是 n就是总节点数 n-1-(a+b+c)就是用总节点数减去u这个子树的节点数,然后求这a b c up 的size的max,更新ans即可,每一次dfs返回值一定要返回sum(所以子树) 这样对于u搜到 a a再往下搜,那么a往下搜返回的就是a这棵树的size。dfs的过程中 因为是从上往下的搜索,既然是无向边,可以任意选一个点为根节点往下搜,注意要构建bool vis数组,每一次搜到这个结点是标记一下,避免向上重复搜索。
就得到关键dfs代码:
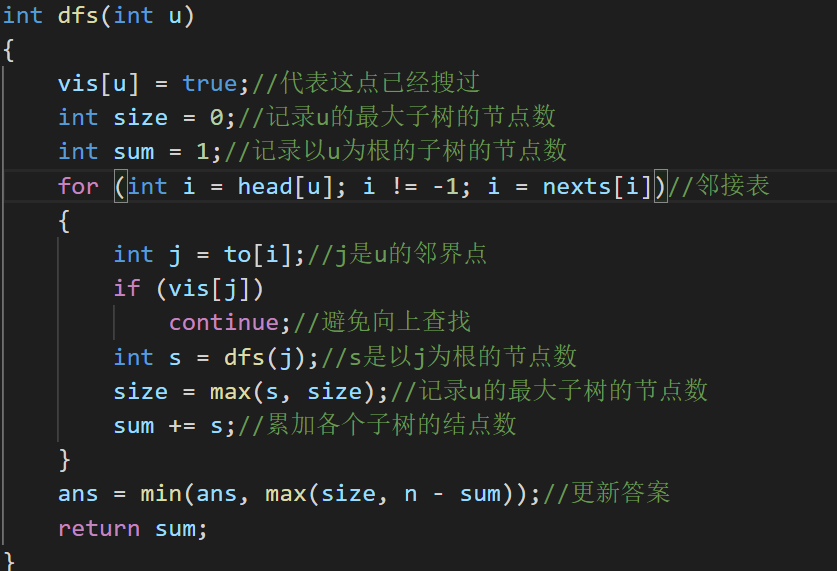
总代码:
1 #include<iostream> 2 #include<algorithm> 3 using namespace std; 4 const int N = 10010, M = N * 2; 5 int n, ans=N;//ans记录最长路径的长度 要初始化为大一点 6 bool vis[N];//记录是否被搜索过 7 int head[N], to[M], nexts[M], index;//邻接表 8 void add(int a, int b)//邻接表存储 9 { 10 to[++index] = b; 11 nexts[index] = head[a]; 12 head[a] = index; 13 } 14 int dfs(int u) 15 { 16 vis[u] = true;//代表这点已经搜过 17 int size = 0;//记录u的最大子树的节点数 18 int sum = 1;//记录以u为根的子树的节点数 19 for (int i = head[u]; i != -1; i = nexts[i])//邻接表 20 { 21 int j = to[i];//j是u的邻界点 22 if (vis[j]) 23 continue;//避免向上查找 24 int s = dfs(j);//s是以j为根的节点数 25 size = max(s, size);//记录u的最大子树的节点数 26 sum += s;//累加各个子树的结点数 27 } 28 ans = min(ans, max(size, n - sum));//更新答案 29 return sum; 30 } 31 int main() 32 { 33 memset(head, -1, sizeof(head)); 34 cin >> n; 35 for (int i = 1; i < n; ++i) 36 { 37 int a, b; 38 cin >> a >> b; 39 add(a, b); 40 add(b, a); 41 } 42 dfs(1);//任取一个点 开始深搜 43 cout << ans << endl; 44 return 0; 45 }


