动态规划：Codeforces Round #336 (Div. 1)607B.Zuma 区间DP

607B.Zuma

 

 题目大意

　　　　就是给你一个数组，每次只能删除里面的回文子串 1 11 121 都算，求删完整串的最少删除次数.我们可以构建区间DP数组dp[i][j],并得出状态转移方程：当s[i]==s[j]时dp[i][j]=dp[i+1][r-1]，因为就相当于删里面的回文时顺便删了外面两个对称的，外面两个对称的端点可以和里面的回文再次构成回文，但这里要注意当s[i]==s[j]时,如果区间长度是2，则dp[i][j]=1要特判，如果s[i]!=s[j]时候，我们就相当于把i j 区间割成几块，分别删除回文，最后求和。

　　　　状态转移方程：

　　　　

 

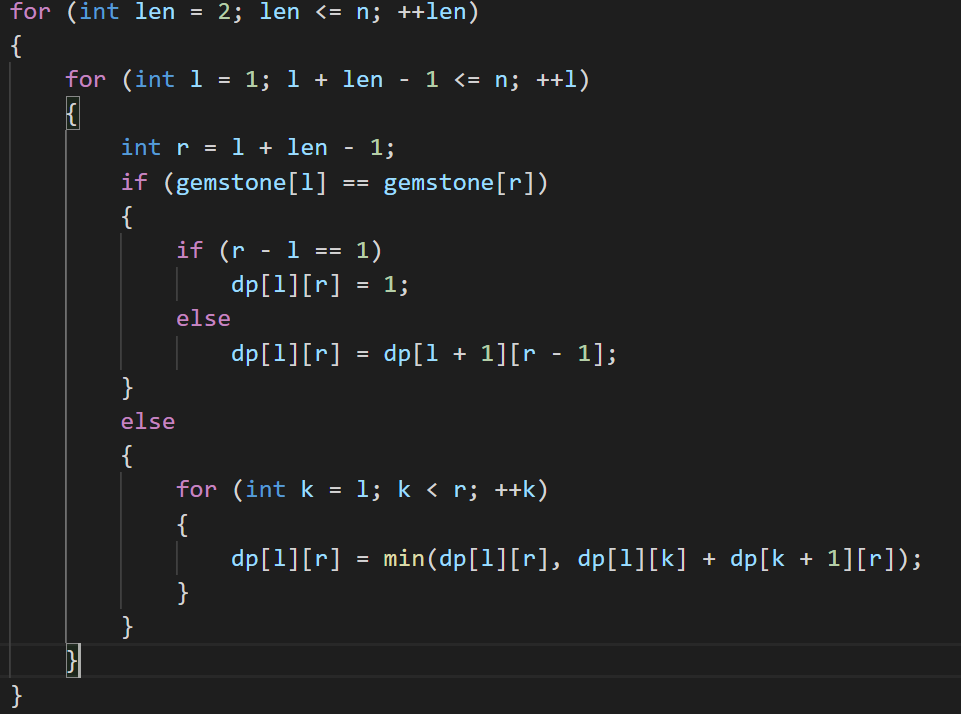
 但这里其实存在错误的地方，我第一次提交的时候错了，错在哪呢？我调试了一下，得出结论。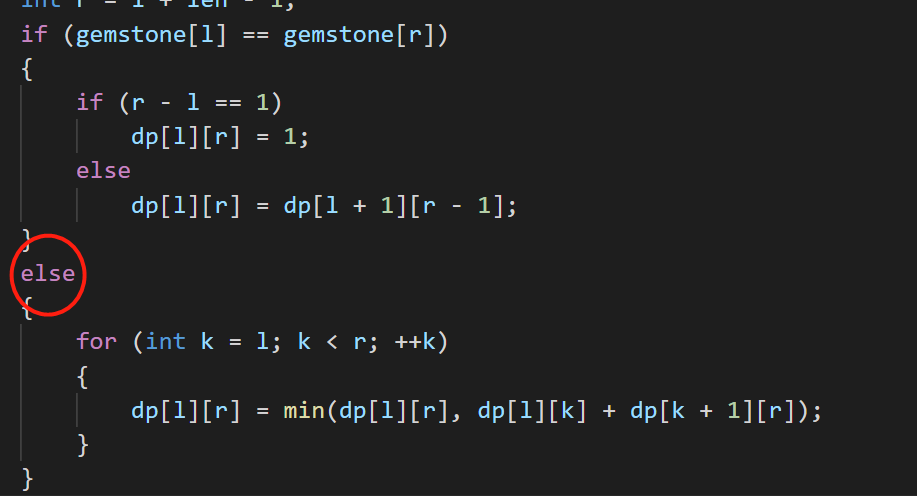

 

 错在这边，其实对于s[l]==s[r]的dp[l][r]，他虽然可以等于dp[l+1][r-1],但是dp[l+1][r-1]并非是最优解，可能把dp[l][r]拆成两块删除的步骤更少，所以不应该加else，对于每种情况都应该加一个切割区间判断最优解。

所以对的状态转移code：

 

 

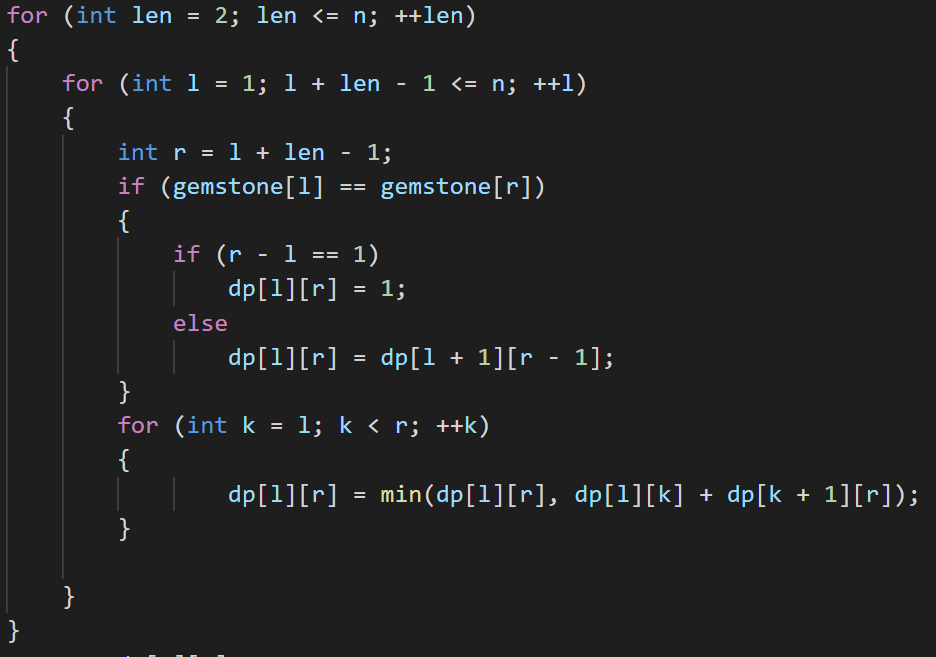
AC代码：

//right
#include<iostream>
#include<cmath>
#include<algorithm>
#include<vector>
#include<cstring>
#include<string>
using namespace std;
const int maxn = 5*1e2+5;
int gemstone[maxn];
int dp[maxn][maxn];
int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    if (ch > '9' || ch < '0')
    {
        f = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9')
    {
        x = (x << 3) + (x << 1) + ch - '0';
        ch = getchar();
    }
    return x * f;
}
int main()
{
    int n = read();
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= n; ++j)
            dp[i][j] = 0xfffffff;//求最小值，初始化为最大值
    for (int i = 1; i <= n; ++i)gemstone[i] = read(),dp[i][i]=1;
    for (int len = 2; len <= n; ++len)
    {
        for (int l = 1; l + len - 1 <= n; ++l)
        {
            int r = l + len - 1;
            if (gemstone[l] == gemstone[r])
            {
                if (r - l == 1)
                    dp[l][r] = 1;
                else
                    dp[l][r] = dp[l + 1][r - 1];
            }
            for (int k = l; k < r; ++k)
            {
                    dp[l][r] = min(dp[l][r], dp[l][k] + dp[k + 1][r]);
            }

        }
    }
    cout << dp[1][n];
    return 0;
}