动态规划：P3146 [USACO16OPEN]248 G

 [USACO16OPEN]248 G

 

 思路与推导过程:

　　　　这题还是挺细节的,是一题区间dp,我们构建的dp[i][j]并不是代表i j 区间内能合成的最优值，而是代表能这个区间能完全合并为一个什么数，如果不行，这个区间的DP值仍然是一开始赋的-inf,一个巨小值。我们为什么要这么构建呢，如果构建的是区间中最大值，那么最后答案是我们常规的dp[1][n],但是这样实际上是错误的比如1 2 2 1 2 2 ,对于1->3这个区间我们认为能合并的最优值是2+1=3,4->6这个区间算出来也是2+1=3，所以我们再算1->6这个区间时我们用1->,4->6这个两个区间来合并算出来的最优值是3+1=4，但实际上这样是错的，2 2 1 2 2,2 2 就算合并了，两个3中间隔了一个1根本不能合并，所以我们为了避免出现这样的考虑，我们改变dp定义的含义，dp[][]代表这个区间能完全合并成一个数得情况，所以相邻的两个区间，只有都能完全合并成一个数，并且一样在能互相转移，如果这个区间的dp值很小，是初始化的-inf，那么说明这个区间无法完全合成一个数，就不算这个区间，然后我们定义一个ans，对于每一个区间的合出来的数，来更新ans，最后ans就是求解的答案，并非dp[1][n].

　　　　关键DP状态转移：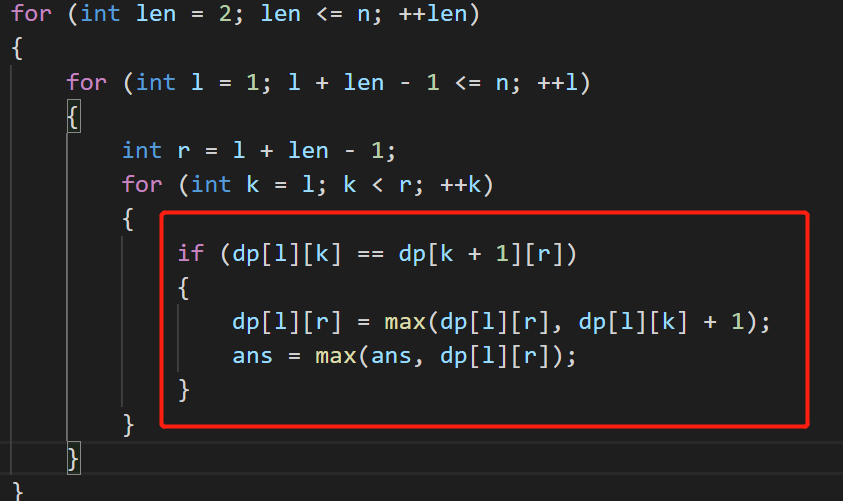

 

 完整AC代码：

#include<iostream>
#include<cmath>
#include<algorithm>
#include<vector>
#include<cstring>
#include<string>
using namespace std;
const int maxn = 300;
int a[maxn];
int dp[maxn][maxn];
int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    if (ch > '9' || ch < '0')
    {
        f = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9')
    {
        x = (x << 3) + (x << 1) + ch - '0';
        ch = getchar();
    }
    return x * f;
}
int main()
{
    int n = read();
    int ans = -0xffffff;
    for (int i = 1; i <= n; ++i)a[i] = read(),dp[i][i]=a[i];
    for (int len = 2; len <= n; ++len)
    {
        for (int l = 1; l + len - 1 <= n; ++l)
        {
            int r = l + len - 1;
            for (int k = l; k < r; ++k)
            {
                if (dp[l][k] == dp[k + 1][r])
                {
                    dp[l][r] = max(dp[l][r], dp[l][k] + 1);
                    ans = max(ans, dp[l][r]);
                }
            }
        }
    }
    cout << ans;
    return 0;

}