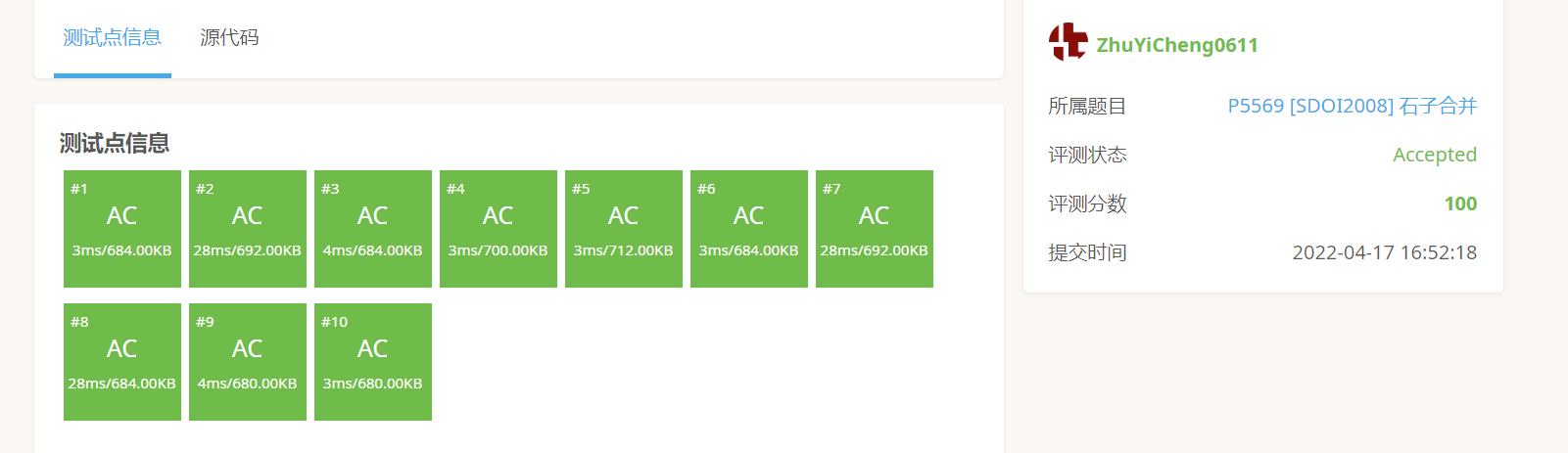
动态规划:P5569 [SDOI2008] 石子合并 GarsiaWachs算法
P5569 [SDOI2008] 石子合并

这题就是P1775石子合并的数据加强版,我们那题采用的是区间DP,时间复杂度为O(n3) (4*1e4)的三次方=1.6*1e13,显然超时。这里就必须用一个算法,叫做GarsiaWachs算法,可以降低时间复杂度至n2甚至nlogn.
GarsiaWachs算法:他的做法就是对于一个序列a,先int ans=0,然后从左到右找到a[k-1]<a[k+1],将a[k]和a[k-1]合并成一个新的元素a[temp],从a[k-1]向左寻找,找到第一个比他大的,插入在他后面,ans+=a[temp],注意要把a[-1]和a[终点]定义为无穷大,方便寻找插入。然后再重复这个操作,直到序列中没有a[k-1]<a[k+1].原理我也不会推导,只知道这么个结论。
这是我的代码:利用stl来操作,但是要开O2优化,否则只有70分,T3个点。
1 //GarsiaWachs 2 //开O2 3 #include<iostream> 4 #include<cmath> 5 #include<algorithm> 6 #include<vector> 7 #include<climits>//INT_MAX的头文件 8 using namespace std; 9 int read() 10 { 11 int f = 1; 12 int ans = 0; 13 char c = getchar(); 14 if (c > '9' || c < '0') 15 { 16 f = -1; 17 c = getchar(); 18 } 19 while (c >= '0' && c <= '9') 20 { 21 ans = (ans << 1) + (ans << 3) + (c - '0'); 22 c = getchar(); 23 } 24 return f * ans; 25 } 26 int main() 27 { 28 int n; 29 n = read(); 30 vector<int>v; 31 v.push_back(INT_MAX - 1); 32 for (int i = 1; i <= n; ++i) 33 { 34 v.push_back(read()); 35 } 36 v.push_back(INT_MAX); 37 int k, j, temp, sum = 0; 38 while (n-- > 1) 39 { 40 for (k = 1; k <= n; ++k) 41 { 42 if (v[k - 1] < v[k + 1]) 43 break; 44 } 45 temp = v[k - 1] + v[k]; 46 for (j = k - 1; j >= 0; --j) 47 { 48 if (v[j] > temp) 49 break; 50 } 51 v.erase(v.begin() + k - 1);//删掉k-1; 52 v.erase(v.begin() + k - 1);//删掉k 53 v.insert(v.begin() + j + 1, temp);//插入和 54 sum += temp; 55 } 56 cout << sum; 57 return 0; 58 59 }
没开O2: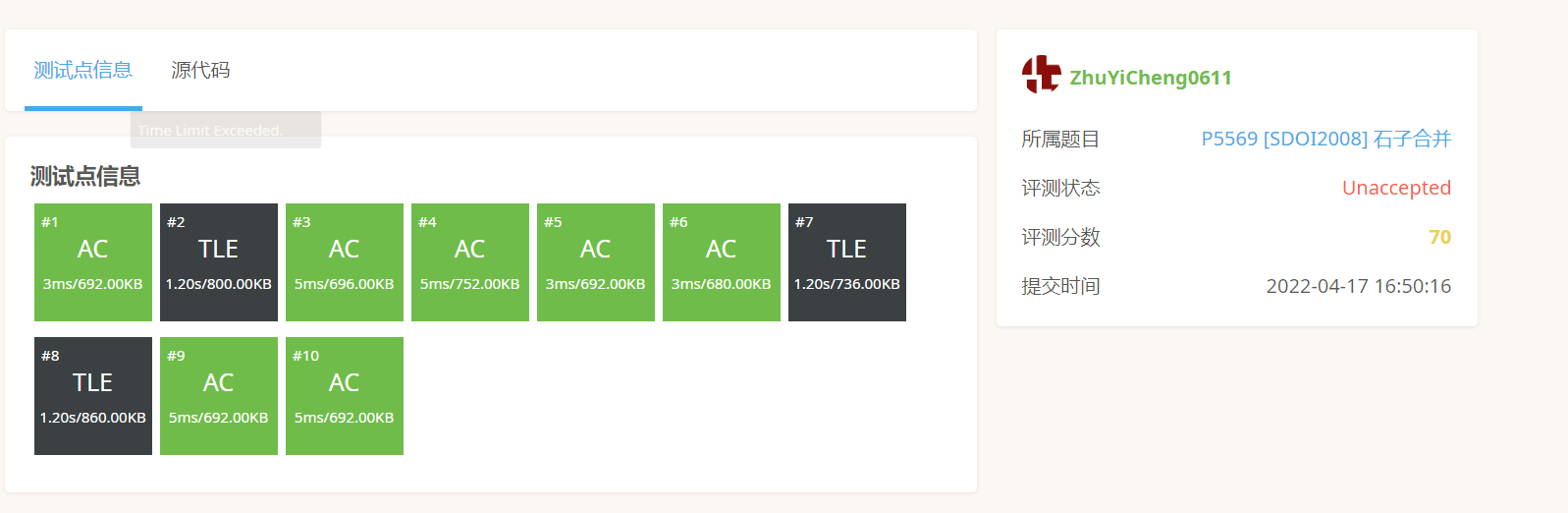
开O2:
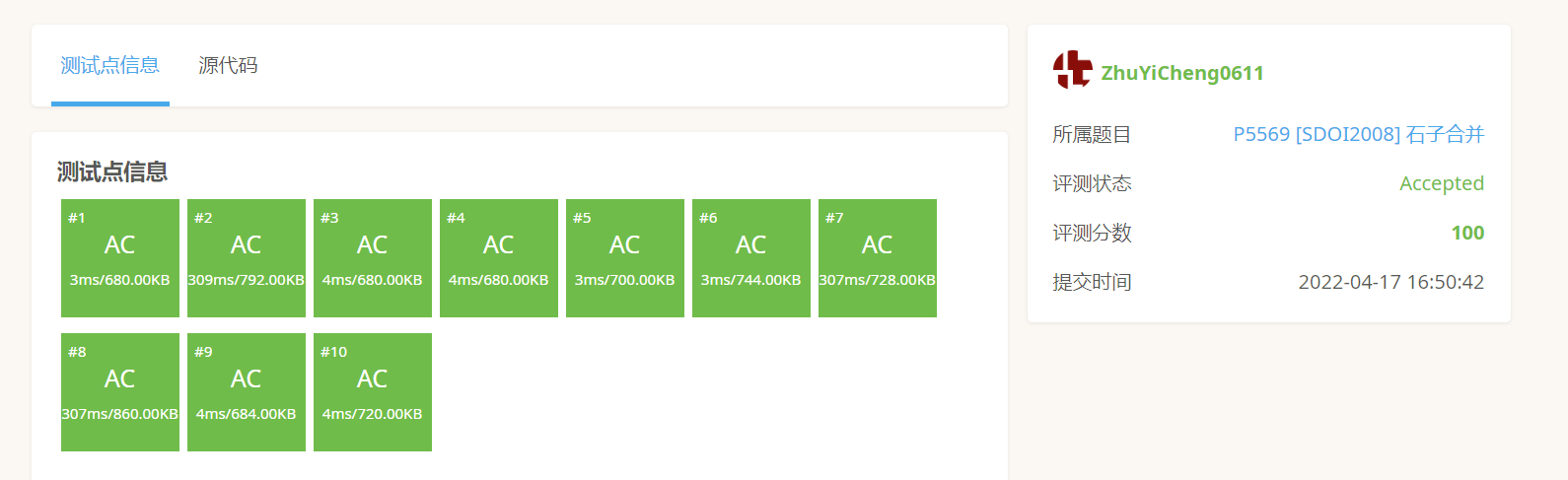
最后补充一下:这个GarsiaWachs算法的标准代码模板,时间复杂度也特别低,高效通过,但是我看了很久也理解不了他的原理。
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int maxn=50005; 4 5 int n; 6 int a[maxn]; 7 int num; 8 int ans; 9 10 void combine(int k){ 11 12 int temp=a[k]+a[k-1]; 13 ans+=temp; 14 for (int i=k;i<num-1;i++){ 15 a[i]=a[i+1]; 16 } 17 num--; 18 19 int j=0; 20 for (j=k-1;j>0&&a[j-1]<temp;j--){ 21 a[j]=a[j-1]; 22 } 23 a[j]=temp; 24 25 while (j>=2&&a[j]>=a[j-2]){ 26 int d=num-j; 27 combine(j-1); 28 j=num-d; 29 } 30 } 31 32 int main() 33 { 34 cin >> n; 35 for (int i=0;i<n;i++){ 36 cin >> a[i]; 37 } 38 num=1; 39 ans=0; 40 for (int i=1;i<n;i++){ 41 a[num++]=a[i]; 42 while (num>=3&&a[num-3]<=a[num-1]){ 43 combine(num-2); 44 } 45 } 46 while (num>1){ 47 combine(num-1); 48 } 49 50 cout << ans << endl; 51 }