动态规划：P1775石子合并（弱化版）区间DP、前缀和

P1775石子合并（弱化版）

题目：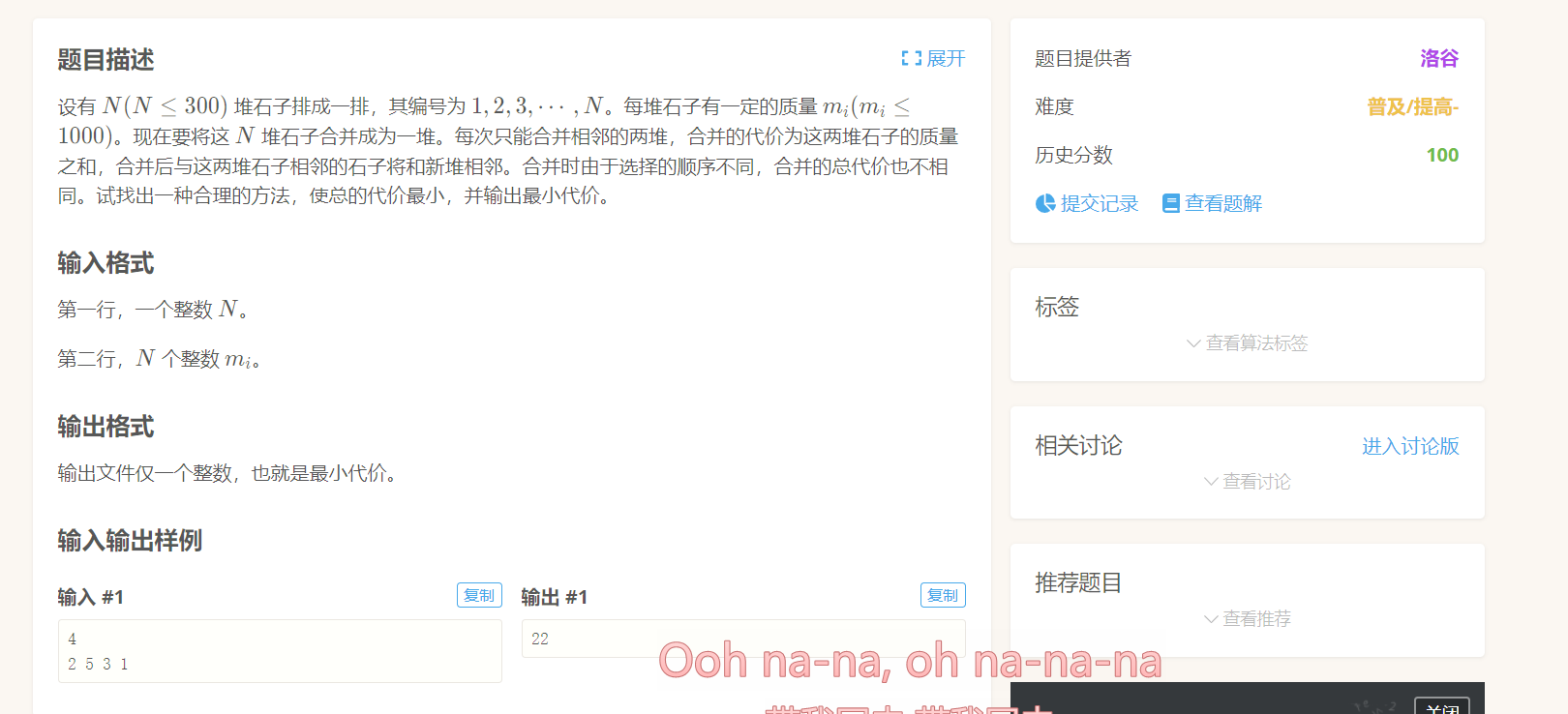

 

 分析一下：

　　　　这是一题最经典的区间DP，也是我学习区间DP的第一题。做题思路是构建DP数组dp[i][j]，i、j分别代表区间的左右端点，思考状态转移方程，对于一个区间dp[i][j]，（注意这里的区间并没有大小关系，只是从这一排石头上截取一部分的意思），把这个区间分割成两个，dp[i][i+k],dp[i+k+1][j]，dp[i][j]一定是从这两堆石头合并起来的，也就是两个区间的代价合并起来的，但一定还要加上新的代价，也就是这两堆石子的总质量，我们可以用前缀和数组pre[j]-pre[i-1]来，但是我们k不确定，所以就要用一层循环来算出max值，所以得出状态转移方程dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+pre[j]-pre[i]);j>k>=i.，区间dp的思路就是先算出小区间的最优解在推出大区间的最优解，最后答案就是dp[1][n]，整个区间的最优解，原因举例也就是算出长度为2的区间，长度为3会割成1 2 、2 1。必须要知道2，后面同理。所以最外层循环就要循环len，区间长度，从2->len.第二层循环区间的左端点l，知道左端点知道长度就可以算出右端点，在加上最内层循环，枚举分割点，注意分割点的取值是在左端点l 和右端点 r之间，并且注意r的取值<=n，推出l的取值 l+len-1<=n。取值范围是这题很需要注意的点，第二还要注意DP的边界条件和初始化问题：求最小代价，就把dp[i][j]初始化为INT_MAX，或者一个很大的值。这样才能算出最小值，注意dp[i][i]一定要初始化为0，因为单单一堆的时候代价为0，自己不用和自己合并。

　　　　上代码：

#include<iostream>
#include<cstring>
#include<string>
#include<algorithm>
#include<cmath>
using namespace std;
const int maxn =305;
int dp[maxn][maxn];
int a[maxn];
int pre[maxn];
int main()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; ++i)
    {
        cin >> a[i];
        pre[i] = pre[i - 1] + a[i];
    }
    for (int len = 2; len <= n; ++len)
    {
        for (int l = 1; l + len - 1 <= n; ++l)
        {
            int r = l + len - 1;
            dp[l][r] = 0x7fffffff;//算最小值的时候给一个大值 便于计算最小值
            for (int k = l; k < r; ++k)
            {
                
                dp[l][r] = min(dp[l][r], dp[l][k] + dp[k + 1][r] + pre[r] - pre[l - 1]);
            }
        }

    }
    cout << dp[1][n];
    return 0;

}