动态规划||单调队列 LeetCode1438.绝对差不超过限制的最长连续子数组
1438.绝对差不超过限制的最长连续子数组
题目大意就是求最大连续的区间,使最大值减最小值小于等于limit.
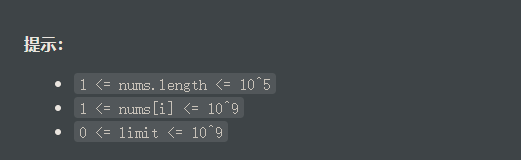
数据范围:
一、Binary Tree
考虑枚举每一个区间,记录每一段长度并且更新ans,每一段长度里面都得满足max-miin<=limit,不满足就把删掉区间的左端点值,直到满足。外层循环遍历每一个区间,这题因为n=1e5,所以不能用n2的算法,内层不能用O(n)的算法,就想到用multiset,logn的复杂度删除不满足的,并且最大值最小值就是区间端点。总的时间复杂度就是O(n*logn)
上代码:
1 //binary tree 2 class Solution { 3 public: 4 int longestSubarray(vector<int>& nums, int limit) { 5 int n = nums.size(); 6 multiset<int>m; 7 int l = 0; 8 int ans = 0; 9 for (int r = 0; r < n; ++r) 10 { 11 m.insert(nums[r]);//区间直接扩展 12 while (*rbegin(m) - *begin(m) > limit) 13 m.erase(m.equal_range(nums[l++]).first);//删除区间最左边的数字 这样后面可以加进去更多的数字 14 ans = max(ans, r - l + 1); 15 } 16 return ans; 17 } 18 };
二、Monotonic queue
对于每一个子序列,都可以用单调队列解决问题,建立两个单调队列,一个存最大值,一个存最小值,最大值队列递减,最小值队列递增,所以对于每个序列就只要最大值队列的队头减去最小值序列的队头看是否满足<=limit,如果不满足,就把两个序列中靠最左边的元素出队,l++,l就是队列的左端点,r就是循环每个元素,则队列每次的长度就是l-r+1,每次更新ans即可。
代码:
1 //monotonic queue 2 class Solution { 3 public: 4 int longestSubarray(vector<int>& nums, int limit) { 5 deque<int>max_q; 6 deque<int>min_q; 7 int ans = 0; 8 int l = 0; 9 int n = nums.size(); 10 for (int r = 0; r < n; ++r) 11 {//10,1,2,4,7,2 12 while (!min_q.empty() && nums[r] < min_q.back()) 13 min_q.pop_back(); 14 while (!max_q.empty() && nums[r] > max_q.back()) 15 max_q.pop_back(); 16 min_q.push_back(nums[r]); 17 max_q.push_back(nums[r]); 18 while (max_q.front() - min_q.front() > limit)//并不会把一个deque删空的情况,删的话都是删靠左边的元素,两个deque起码剩下一个共同元素,并且共同元素的差=0<limit 19 { 20 if (max_q.front() == nums[l])max_q.pop_front(); 21 if (min_q.front() == nums[l])min_q.pop_front(); 22 ++l; 23 } 24 ans = max(ans, r - l + 1); 25 26 } 27 return ans; 28 } 29 };