动态规划||单调队列：LeetCode1425.带限制的子序列和

1425.带限制的子序列和

 

 意思就是寻找最大子区间和，子区间的每一个相邻元素可以下表最多相差k.

一、

想到求最大连续子区间和O（n）的方法，但是这题显然状态转移方程并不是dp[i]=max(dp[i-1],0)+a[i],他可以跳过最多k-1个元素 所以里面应该嵌套一层循环 for(int j=1->k)dp[i]=max(dp[i-j],dp[i]);循环后dp[i]=max(dp[i],0)+a[i];时间复杂度为O(n*k).但我们看数据范围：

 

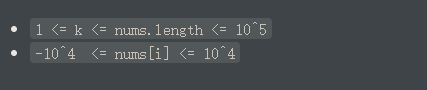
 n和k都可以达到1e5，则时间复杂度最多达到1e10，显然超时，需要改进算法。

二、Binary tree

我们就想到用binary tree ,用multiset这个可以自动排序来存储每i个的前k个，有点想slide window,长度为k的窗口一直在滑动，然后每次dp[i]取multiset中的最大值，如果最大值都小于0就取0，加上a[i]即可。外层循环dp[i]，时间复杂度为n,内层循环利用multiset的equal_range，时间复杂度为logk,所以总的时间复杂度为O(n*logk),不会超时。

上代码:

//Binary tree  nlogk
class Solution {
public:
    int constrainedSubsetSum(vector<int>& nums, int k)
    {
        const int n = nums.size();
        multiset<int>m{-0x7fffffff};//必须得给这个初始化一个最小值 !!这样就不用检查multiset是不是空的
        vector<int>dp(n);
        int ans = -0x7fffffff;
        for (int i = 0; i < n; ++i)
        {
            if (i > k)
                m.erase(m.equal_range(dp[i - (1 + k)]).first);
            dp[i] = max(*rbegin(m), 0) + nums[i];//在这地方如果multiset是空的就会出错 加一个最小值在m中防止报错
            m.insert(dp[i]);
            ans = max(dp[i], ans);
        }
        return ans;
    }
};

 

 

三、Monotonic queue

也可以利用单调队列，时间复杂度为O（n）

class Solution {
public:
    int constrainedSubsetSum(vector<int>& nums, int k)
    {
        const int n = nums.size();
        vector<int>dp(n);
        deque<int>q;//存的是index 下标
        int ans = -0x7fffffff;
        for (int i = 0; i < n; ++i)
        {
            if (i > k && q.front() == i - (k + 1))//可以选择坐标相差k 但相差k+1就不行了 得从窗口中出队
                q.pop_front();
            dp[i] = (q.empty() ? 0 : max(dp[q.front()], 0)) + nums[i];
            while (!q.empty() && dp[i] >= dp[q.back()])
                q.pop_back();
            q.push_back(i);
            ans = max(ans, dp[i]);
           
        }
        return ans;
    }
};