动态规划:Educational Codeforces Round 123 (Rated for Div. 2)C. Increase Subarray Sums (最大连续区间和)
C. Increase Subarray Sums
传送门:Problem - 1644C - Codeforces

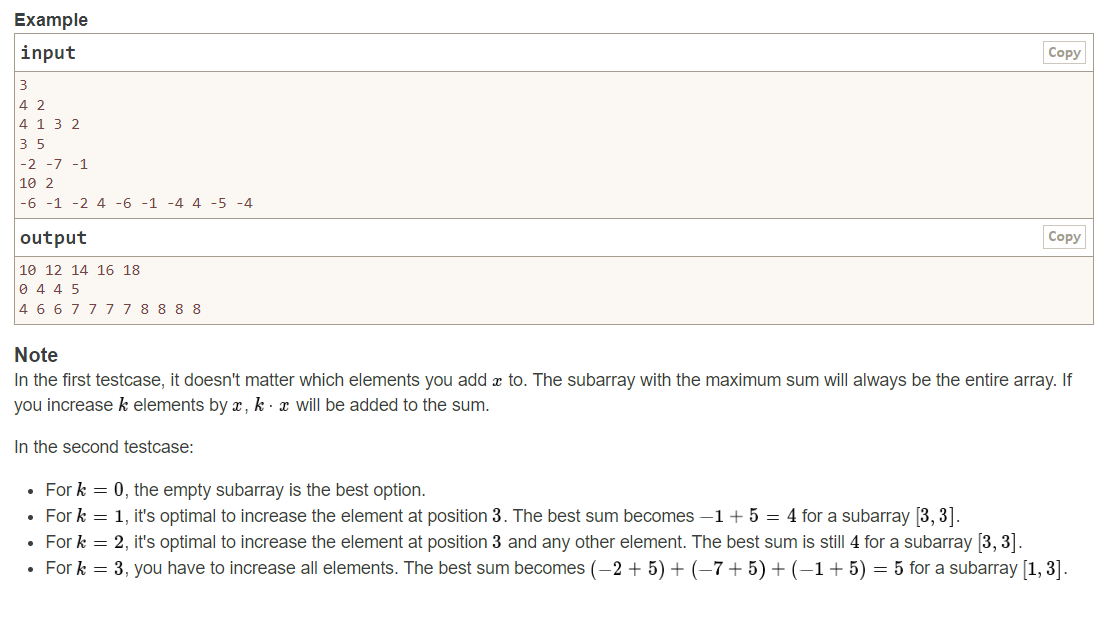
题目大意就是:给你一个序列,算出序列和为sum,求是否有连续区间和大于等于sum,有就输出NO,否则YES,并且连续区间不能是[1,n],也就是整个序列,我的思路就是构建两个DP数组,既然区间不能是1->n,那么一个dp从1->n-1,第二个从2->n,求dp[i],i代表以i结尾的区间的最大连续区间和,有大于等于sum的直接输出NO,最后都没有的话就输出YES。本质上就是一个最大连续区间和的问题。
上代码:
1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #include<algorithm> 5 #include<map> 6 using namespace std; 7 const int maxn = 1e5 + 5; 8 const int inf = -0x7FFFFFFF; 9 long long a[maxn]; 10 long long dp1[maxn]; 11 long long dp2[maxn]; 12 long long read() 13 { 14 long long x = 0, f = 1; 15 char ch = getchar(); 16 if (ch > '9' || ch < '0') 17 { 18 f = -1; 19 ch = getchar(); 20 } 21 while (ch >= '0' && ch <= '9') 22 { 23 x = (x << 3) + (x << 1) + ch -'0'; 24 ch = getchar(); 25 } 26 return x * f; 27 } 28 long long max(long long a, long long b) 29 { 30 if (a > b) 31 return a; 32 else return b; 33 } 34 int main() 35 { 36 long long t; 37 t = read(); 38 while (t--) 39 { 40 long long n; 41 n = read(); 42 long long sum = 0; 43 for (int i = 0; i <= n; ++i)dp1[i] = inf, dp2[i] = inf; 44 for (int i = 1; i <= n; ++i) 45 { 46 a[i] = read(); 47 sum += a[i]; 48 } 49 bool flag = 0; 50 for (int i = 1; i < n; ++i) 51 { 52 dp1[i] = max(dp1[i - 1], 0) + a[i]; 53 if (dp1[i] >= sum) 54 { 55 flag = 1; 56 break; 57 } 58 59 } 60 if (!flag) 61 { 62 for (int i = 2; i <= n; ++i) 63 { 64 dp2[i] = max(dp2[i - 1], 0) + a[i]; 65 if (dp2[i] >= sum) 66 { 67 flag = 1; 68 break; 69 } 70 } 71 } 72 if (flag)cout << "NO"<<endl; 73 else cout << "YES"<<endl; 74 75 } 76 return 0; 77 78 }
0X7FFFFFFF代表INT最小的。挺好用的,一般定义为inf。


