动态规划+前缀和：Educational Codeforces Round 123 (Rated for Div. 2)C. Increase Subarray Sums

Educational Codeforces Round 123 (Rated for Div. 2)

C. Increase Subarray Sums

传送门：Problem - C - Codeforces

 

 

 

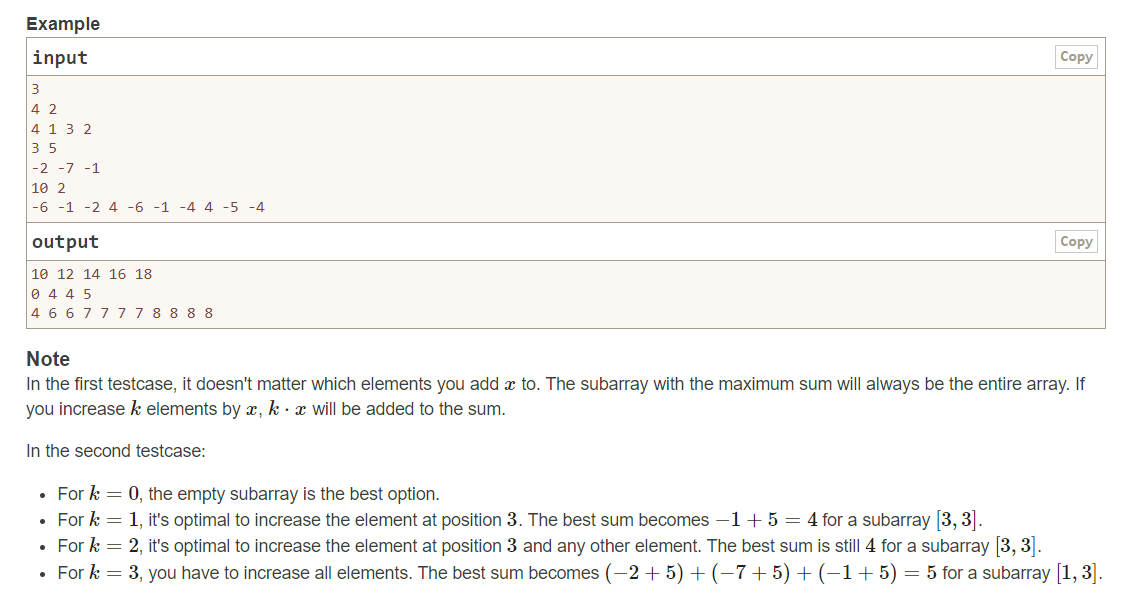
 　　　　题目大意就是：给你一个数组a,长度为n,再给你一个数为k,定义ans数组,求ans[i]的每个元素，i从0到n.ans[i]代表给数组中i个元素加上k后的最大连续子区间和。最大子区间长度可以是0，也就是一个数都不要。可以想：当i=0时，就是求序列的最大子区间和，当i!=0时，就不是了单纯的求最大子区间和再加上i*x了，因为如果最大子区间和长度是0，那么0个元素，就不能加上x，但是如果长度是1，元素是-1 ，加上x后可能大于0，所以就需要运用到动态规划，推出最优解.

　　　　做法及其思路:这里有两个做法.

一、DP

　　　　构建dp数组DP[i][j],i代表以最外层循环,循环每一个元素，也就是i:1->n,内层循环j代表，循环的是对于这个数结尾的子序列区间，加上j个x后的最优解，所以就是从j:1->n.。因为对于ans[0]来说，就只是单纯的求最大连续区间和。所以ans[0]放在外层循环求,每次用max函数更新。复习一下求最大连续区间和的做法，构建一个dp[]数组,对于每一个a[i],dp[i]=max(dp[i-1],0)+a[i];意思是如果dp[i-1]<0,那么前面的都不要，只要自己a[i]，如果前面的大于0，就取千米爱你的dp[i-1]加上自身的a[i]，然后每次算出来dp[i],都要ans都要比较更新一下ans=max(ans),但这里要写成二维的形式,dp[i][0],代表一个x都没加上。对于其他ans[i]，i>0，在内层循环中寻找最大的dp[i][j]就是，内层循环的转移方程 int b,c。

　　for int j 1to n

　　　b=max(dp[i-1][j],0)+a[i]

　　　c=max(dp[i-1][j-1],0)+a[i]+x;

　　　dp[i][j]=max(b,c);

　　　　原理：对于一个dp[i][j]      他一定是从 dp[i-1]，也就是上一层算出来的最大连续子区间，中选择 ①已经上一层算出来已经加上j个x后的最大连续子区间，再加上这层的a[i]，如果上一层小于0，那么就不要上一层的最大连续子区间，所以有一个max（..，0）函数。②从上一层的已经加上j-1个x后，这一层加上x和a[i]，同样上一层小于0，舍去。     虽然是这么描述的，但实际上上一层不一定加入了j个x或j-1个x，对于外层循环i，每次循环一个i，最多加入一个x，因为一个元素只能加上一个x，但也无关紧要，可以继续算下去，后面遍历到i等于...，一定会加上j个x，算出更好的答案，把前面ans[i]=dp[i][j]，但这个i<j 实际上没加上足够的j个x,的ans[i]用max函数更新掉。

　　　　状态转移方程代码：非常关键！可以好好结合代码和我的思路原理想一想.

　　　　

for (int i = 1; i <= n; ++i)
        {
            dp[i][0] = max(dp[i - 1][0], 0) + a[i];
            ans[0] = max(dp[i][0], ans[0]);
            for (int j = 1; j <= n; ++j)
            {
                one = max(dp[i - 1][j],0) + a[i];
                two = max(dp[i - 1][j - 1],0) + a[i] + x;
                dp[i][j] = max(one, two);
                ans[j] = max(dp[i][j], ans[j]);
            }
        }

上总代码：

#include <algorithm>
#include <iostream>
#include<cmath>
#include<cstring>
using namespace std;
const int maxn = 5005;
int read()
{
    int f = 1;
    int x = 0;
    char c = getchar();
    if (c > '9' || c < '0')
    {
        f = -1;
        c = getchar();
    }
    while (c >= '0' && c <= '9')
    {
        x = (x << 3) + (x << 1) + c - '0';
        c = getchar();
    }
    return f * x;
}
int a[maxn], dp[maxn][maxn], ans[maxn];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t;
    t = read();
    while (t--)
    {
        int n, x;
        n = read(), x = read();
        for (int i = 1; i <= n; ++i)a[i] = read();
        for (int i = 0; i <= n; ++i)//重新初始化dp 和 ans数组
        {
            ans[i] = 0;
            for (int j = 0; j <= n; ++j)
            {
                dp[i][j] = 0;
            }
        }
        int one, two;
        for (int i = 1; i <= n; ++i)
        {
            dp[i][0] = max(dp[i - 1][0], 0) + a[i];
            ans[0] = max(dp[i][0], ans[0]);
            for (int j = 1; j <= n; ++j)
            {
                one = max(dp[i - 1][j],0) + a[i];
                two = max(dp[i - 1][j - 1],0) + a[i] + x;
                dp[i][j] = max(one, two);
                ans[j] = max(dp[i][j], ans[j]);
            }
        }
        for (int i = 0; i <= n; ++i)cout << ans[i] << " ";
        cout << endl;
    }
    return 0;
}

 

二、前缀和做法

　　先用前缀和，利用二重循环算出这个数组每一种长度的连续区间和的最大值len[i]  再用两重循环，最外层循环循环的是算加上0-n个x后的最大值，所以是i从0-n,内层循环遍历所有长度 len[j] +min(i,j)*x;就是所有长度的区间和加上x，加上x的个数必须比取区间长度和外层循环限定的加上x的个数的最小值。

　　思路的关键代码：

　　

 for(int i=0;i<=n;i++)//加上0~n个x后的最大值
        {
            int maxx=-0x3f3f3f3f;
            for(int k=1;k<=n;k++)
            {
                maxx=max(maxx,len[k]+min(k,i)*x);
            }
            printf("%d ",max(maxx,0));
        }

 

完整AC代码：

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=5050;
int a[N];
int len[N];//i长度的数组最最大值
int prefix[N];
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        memset(len,-0x3f,sizeof(len));//要注意，凡是涉及到有负数的东西一定要初始设到最小
        memset(prefix,0,sizeof(prefix));
        int n,x;
        cin>>n>>x;
        for(int i=1;i<=n;i++) cin>>a[i];
        for(int i=1;i<=n;i++) prefix[i]=prefix[i-1]+a[i];//求一个前缀和
        //for(int i=1;i<=n;i++) printf("%d-->\n",prefix[i]);
        for(int i=1;i<=n;i++)//从i位置开始k长度区间的最大值
        {
            for(int k=1;k<=n;k++)//
            {
                if(i+k-1<=n) len[k]=max(len[k],prefix[i+k-1]-prefix[i-1]);
            }
        }
        //printf("\n");
        //for(int i=1;i<=n;i++) printf("%d-->\n",len[i]);
        //printf("\n\n");
        for(int i=0;i<=n;i++)//加上0~n个x后的最大值
        {
            int maxx=-0x3f3f3f3f;
            for(int k=1;k<=n;k++)
            {
                maxx=max(maxx,len[k]+min(k,i)*x);
            }
            printf("%d ",max(maxx,0));
        }
        printf("\n");
    }
    return 0;
}