动态规划：洛谷 P1280 尼克的任务

洛谷 P1280 尼克的任务

 

 

 

 

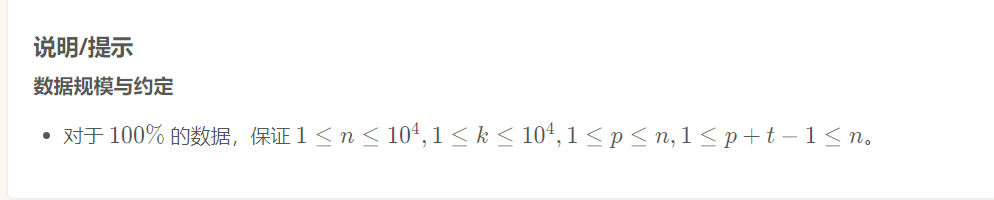
　　　　这是洛谷的一题绿题，考的是动态规划。我们先想状态转移方程，这是个线性的dp，那么可以考虑每一个时间，dp[]就代表0-此时间内的最大闲暇时间，但发现最大闲暇时间，前面的选择会对后面的选择产生影响，有后效性，所以不妨倒着来，从最后一个时间一直递推到第一个，后面选择的任务对前面任务的选择并不会产生影响的。所以我们遍历每一个时间，状态转移方程：如果这个点没有work，那么dp[i]=dp[i+1]+1就是上一个空闲时间+1，如果有，就开一个循环，遍历这个时间点的所有工作worktime[j],dp[i]=max(dp[i+worktime[j]]);

　　　　上代码：

//洛谷 P1280 尼克的任务
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int dp[10005], num[10005], n, k;//num数组存的是这个时间点有几个任务开始
//dp数组存的是从n分钟到这个第i时间的最长休闲时间
struct worktime
{
    int b;
    int l;
}work[10005];//存放工作开始和持续时间的结构体
bool cmp(worktime a, worktime c)
{
    return a.b > c.b;//从大到小排序一下，因为是逆向 从时间大到时间小去DP
}
int main()
{

    cin >> n >> k;
    for (int i = 1; i <= k; ++i)
    {
        cin >> work[i].b >> work[i].l;
        num[work[i].b]++;
    }
    sort(work + 1, work + 1 + k, cmp);//从小到大排序一下
    int x = 1;//这是一个标志，因为下面有任务就要遍历一下这个时间点的所有work，寻找最优解
    //我们干脆引入一个x就是work里面的下标，因为work已经从大到小排序过，所以我们每次只要看work[x],x++，这样每次判断的work[x]会刚好，可以自己举例验证
    for (int i = n; i >= 1; --i)
    {
        if (!num[i])//如果这个时间没有work 那么他的休闲时间就等于前一个休闲时间+1分钟
            dp[i] = dp[i + 1] + 1;
        else//否则就开始循环 找最优解
        {
            for (int j = 1; j <= num[i]; ++j)//循环num[i]次
            {
                dp[i] = max(dp[i], dp[i + work[x].l]);
                x++;
                //如果只有一个任务，那么dp[i]一定等于0，这样也一定会接这个任务，
                //保证了符合题目，有一个任务必须做，有两个以上就max比较，因为i到i+work[x].l的时间在做任务
                //所以i时间的最大休息时间等于i+workx.l；
                //记得++x
            }
        }

    }

    cout << dp[1];//dp[1]就是最终答案
    return 0;

}

 

完美通过：

 

 时间复杂度也只是o(n+k),顺利通过。