动态规划:洛谷 P4933 大师 (一题多解)
洛谷 P4933 大师


题目和数据范围如上。这是洛谷一题普及+/提高的题目,考点是动态规划。有以下几种做法:
一、O(n2 v)
利用三层循环DP,复杂度高,暴力。最外层循环枚举公差,公差的选择:最高的和最矮的差值是公差的最大值,他的负数是公差的最小值。内层有两个循环,枚举两个数是否能构成等差,如果可以,状态转移方程为
dp[i][d]=sum( dp[j][d]+1);(j是所有在i前面的元素),i/j代表的是以i/j结尾的序列,d代表的是公差+20000,因为存在公差为负数的情况,所以我们+20000,全部右移一个区间,缺点是浪费空间。为什么是这个状态转移方程呢,如果i j能构成等差 种类数相当于 j的所有序列的尾巴都加上一个i 数量是dp[j][d],+1就是 和h[i] 和h[ j]两个独自构成一个等差。
上代码:

1 //洛谷 P4933 大师 2 #include<iostream> 3 #include<cmath> 4 using namespace std; 5 int h[1005], dp[1005][40005];//代表的是对于以i结尾的,公差为j+20000最多的可能性 6 const int mo = 998244353; 7 int ans; 8 int main() 9 { 10 int n; 11 cin >> n; 12 int m = -1;//记录max 13 for (int i = 1; i <= n; ++i) 14 cin >> h[i], m = max(m, h[i]); 15 ans += n; 16 for (int i = -m; i <= m; ++i) 17 { 18 for (int j = 1; j <= n; ++j) 19 { 20 21 for (int k = 1; k < j; ++k) 22 { 23 if ((h[j] - h[k]) == i) 24 { 25 dp[j][i + 20000] += dp[k][i + 20000] + 1; 26 27 } 28 } 29 ans += dp[j][i + 20000]; 30 ans %= mo; 31 } 32 33 } 34 cout << ans; 35 return 0; 36 }
·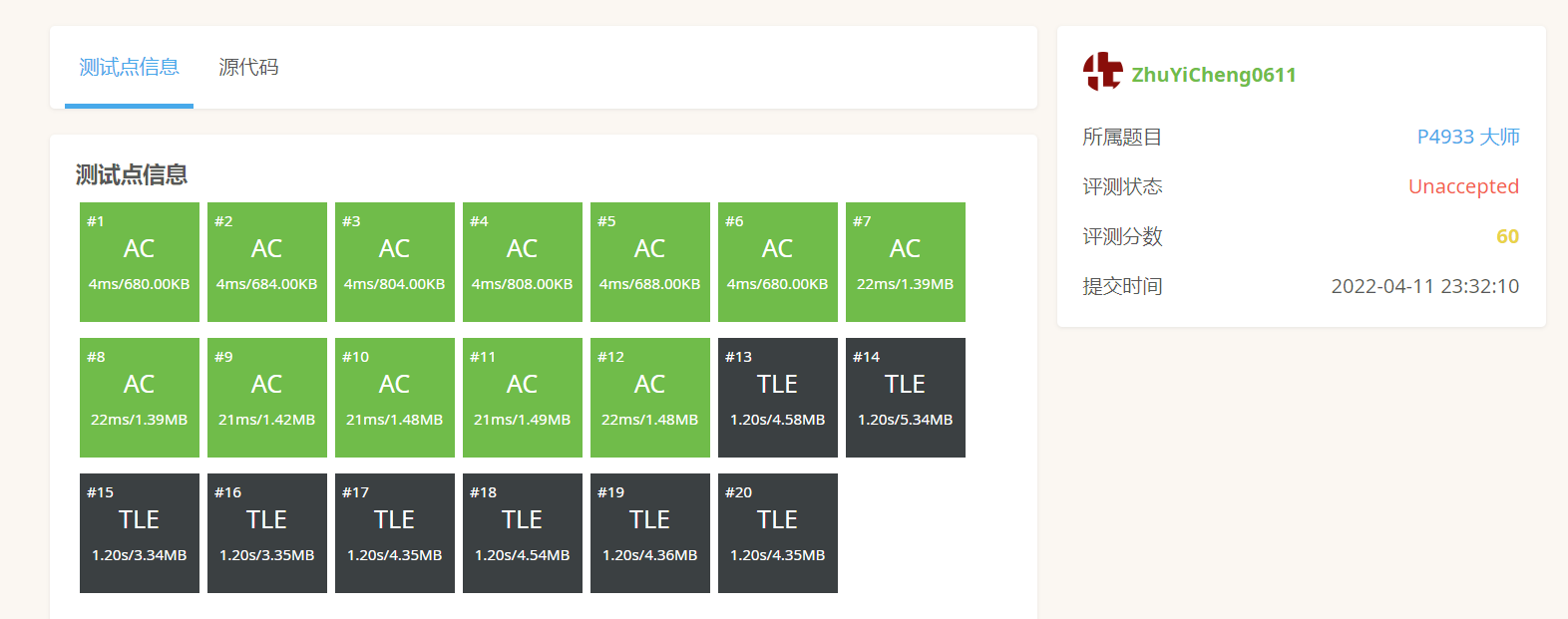
只过了12个测试点,还有8个超时,这样很显然的,毕竟时间复杂度太大了,想着改进算法。
二、O(n3)
DP数组修改一下,dp[i][j],i代表以i结尾的序列,j表示倒数第二个元素是j的序列,这样有两个优点,一:DP的的空间复杂度小了,第二维不用开公差了,公差远大于种类数,空间复杂度高,我们只要用h[i]-h[j]就能表示公差,二:最外层循环不需要枚举公差了,最外面两层循环枚举每一个i 和 j 里面一层循环枚举k,我们让 i>j>k,利用数学结论,如果k j i 构成等差数列,那么h[j]*2=h[i]+h[k];所以h[j]*2=h[i]+h[k]成立时当所以i和j的DP一定是由j 和 k传递来的,并且dp[i][j]+=dp[j][k],因为i j只是相当于在 j k的所有序列的情况的末尾都加上一个 i 。三层循环的时间复杂度为n3,比n2v降低了。
上代码:

1 //洛谷 P4933 大师 2 #include<iostream> 3 #include<cmath> 4 using namespace std; 5 int h[1005], dp[1005][1005];//代表的是对于以j结尾的,上一个是i的种类数 6 const int mo = 998244353; 7 int ans; 8 int main() 9 { 10 int n; 11 cin >> n; 12 for (int i = 1; i <= n; ++i) 13 { 14 cin >> h[i]; 15 dp[0][i] = 1;//表示只有一个时候 有一种可能性 16 } 17 ans += n;//先把都只有一个的时候的可能性加上 18 for (int i = 2; i <= n; ++i)//用两层循环来表示公差 19 for (int j = 1; j < i; ++j) 20 { 21 dp[j][i] = 1;//初始化一下,h[i],h[j]起码能构成一个等差数列 22 for (int k = 1; k < j; ++k) 23 { 24 if (h[j] * 2 == h[i] + h[k])//如果k j i 构成等差数列 25 { 26 dp[j][i] += dp[k][j]; 27 //相当于把以k为倒数第二个,j为倒数第一个的所有序列尾巴上都加上一个i 但是种类数还是不变得 28 dp[j][i] %= mo; 29 30 } 31 } 32 ans += dp[j][i]; //以二维循环的形式累加到ans,这样保证了每一种dp只累加一次到ans 无后效性,所有可能:以i为结尾,j为倒数第二个的每一种可能都遍历到,并且只加一次到ans。 33 ans %= mo; 34 } 35 cout << ans; 36 37 return 0; 38 }
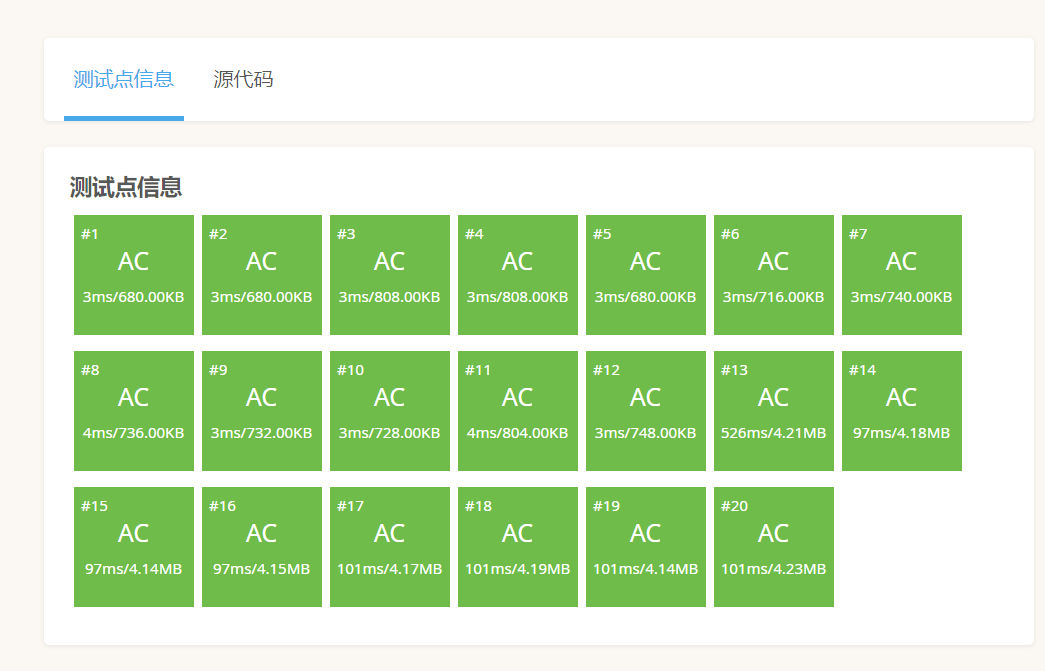
三、O(n2)
根据2的思路,我们还可以继续优化,我们两重循环枚举 i j 那么 i和 j一定会构成一个公差d.所以我们不用表示公差 直接用 i j 的高度差表示公差,两层循环,dp[i][d]的含义改变,i代表结尾,d代表公差,则状态转移方程: dp[i][d]=sum (dp[j][d]+1) j代表所有小于i的数字 状态转移方程同1并且原理相同.
上代码:

1 //洛谷 P4933 大师 2 #include<iostream> 3 #include<cmath> 4 using namespace std; 5 int h[1005], dp[1005][40000];//代表的是对于以i结尾的,公差为j-20000的种类数 6 const int mod = 998244353; 7 int ans; 8 int main() 9 { 10 int n; 11 cin >> n; 12 for (int i = 1; i <= n; ++i) 13 { 14 cin >> h[i]; 15 } 16 int p = 20000; 17 for (int i = 1; i <= n; i++) 18 { 19 ans++;//只有一种的情况 20 for (int j = i - 1; j > 0; j--) 21 { 22 int d = h[i] - h[j] + p; 23 dp[i][d] += dp[j][d] + 1;//加上dp[j][d]是相当于让以h[j]结尾 公差一样的序列 每个尾巴都加上一个h[i] 24 //此时一定还构成等差序列 加上1是要加上h[j] h[i]这个序列 这两个也一定构成等差 25 26 ans += dp[i][d]; 27 28 dp[i][d] %= mod; 29 ans %= mod; 30 } 31 } 32 cout << ans; 33 34 return 0; 35 }
但是提交发现:
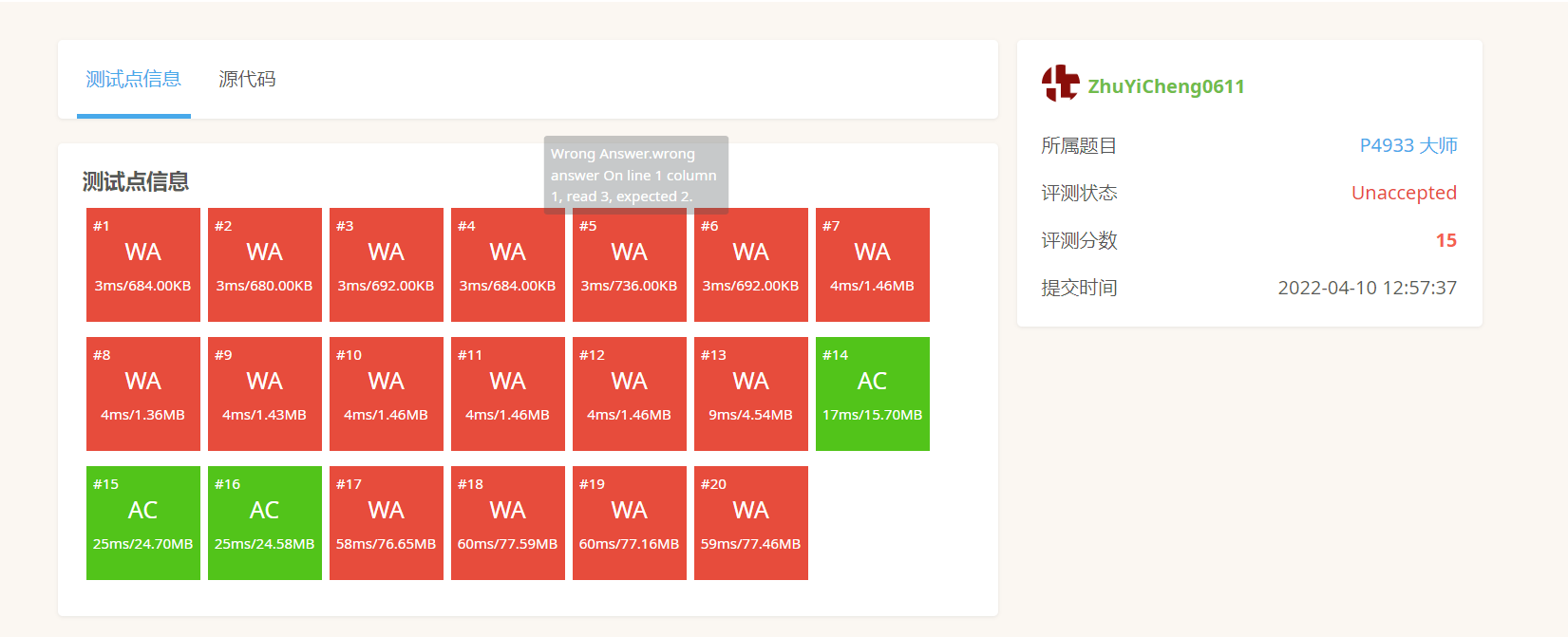
错了。调试检查发现原因,原因在新的代码中注释了,测试案例就是 出现一样的高度的铁塔情况,可以自己试试。
上代码:

1 //洛谷 P4933 大师 2 #include<iostream> 3 #include<cmath> 4 using namespace std; 5 int h[1005], dp[1005][40000];//代表的是对于以i结尾的,公差为j-20000的种类数 6 const int mod = 998244353; 7 int ans; 8 int main() 9 { 10 int n; 11 cin >> n; 12 for (int i = 1; i <= n; ++i) 13 { 14 cin >> h[i]; 15 } 16 int p = 20000; 17 for (int i = 1; i <= n; i++) 18 { 19 ans++;//只有一种的情况 20 for (int j = i - 1; j > 0; j--) 21 { 22 int d = h[i] - h[j] + p; 23 dp[i][d] += dp[j][d] + 1;//加上dp[j][d]是相当于让以h[j]结尾 公差一样的序列 每个尾巴都加上一个h[i] 24 //此时一定还构成等差序列 加上1是要加上h[j] h[i]这个序列 这两个也一定构成等差 25 26 ans += dp[j][d] + 1;//注意点!这个只能加上前一项的dp[j][d] + 1 ,不能加上dp[i][d],因为如果有两个j满足公差一样,那么dp[i][d]的 27 //初始值就并不是0 那么ans直接加dp[j][d] + 1,两个j公差相等的话,则第一次加后dp[i][d]已经不等0,第二次直接加dp[i][d]会把第一次的答案重复加一次 使答案偏大 28 //如果dp的第二个元素是j那么就没事,但这里是d 不同的j可能h[j]相同 所以不行 29 30 dp[i][d] %= mod; 31 ans %= mod; 32 } 33 } 34 cout << ans; 35 36 return 0; 37 }

非常完美,时间复杂度也杠杠的,就是空间复杂度变大了,牺牲空间换时间呀。
四、其实我看了题解,很多都提到这题本来的正解是用nv的时间复杂度,虽然大于n2,但是我也很想思考写出这个算法,奈何实在写不出来,题解中也没有找到有人写了这种算法,只能暂且搁下,灵感来的时候补全nv的代码。他的思路是dp[i]=sum[h[i]-d];sum[h[i]]+=dp[i];sum数组存所有高度为h的dp和,dp[i]数组就等于高度比他矮d的所有dp[]之和,用sum数组来存,代码暂时写不出来,就写一个思路。



