动态规划:洛谷P1439 【模板】最长公共子序列 LCS (转化为LIS的做法,复杂度从n2->nlogn)
洛谷P1439 【模板】最长公共子序列 LCS
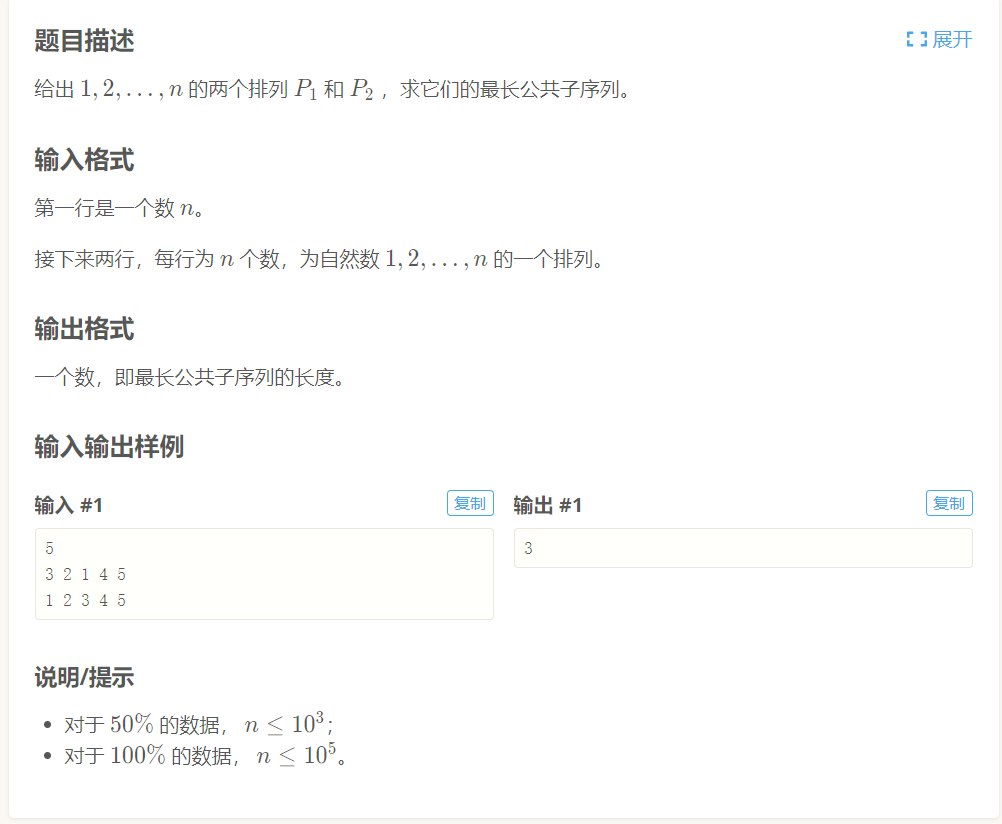
直接利用DP的思路,状态转移方程,构建二维dp数组 dp[i][j] i代表的是第一个数组的前i个 j同理,dp[i][j]代表的是第一个数组前i个和第二个数组前j个的最大公共元素个数,所以可以得出状态转移方程: 如果第i个和第j个不同,则dp[i][j]=max(dp[i-1][j],dp[i][j-1]);如果相同,则dp[i][j]=dp[i-1][j-1]+1;于是我们写出代码:
一、最长公共子序列模板:
代码:
1 //p1439 【模板】最长公共子序列 2 #include<iostream> 3 #include<cstdio> 4 #include<algorithm> 5 using namespace std; 6 const int m = 1e5; 7 int a[m], b[m], dp[10000][10000]; 8 int main() 9 { 10 int n; 11 cin >> n; 12 int len = 1; 13 for (int i = 1; i <= n; ++i)cin >> a[i]; 14 for (int i = 1; i <= n; ++i)cin >> b[i]; 15 for (int i = 1; i <= n; ++i) 16 for (int j = 1; j <= n; ++j) 17 if (a[i] == b[j]) 18 dp[i][j] = max(dp[i - 1][j - 1] + 1, dp[i][j]); 19 else 20 dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]); 21 cout << dp[n][n]; 22 }
提交发现:
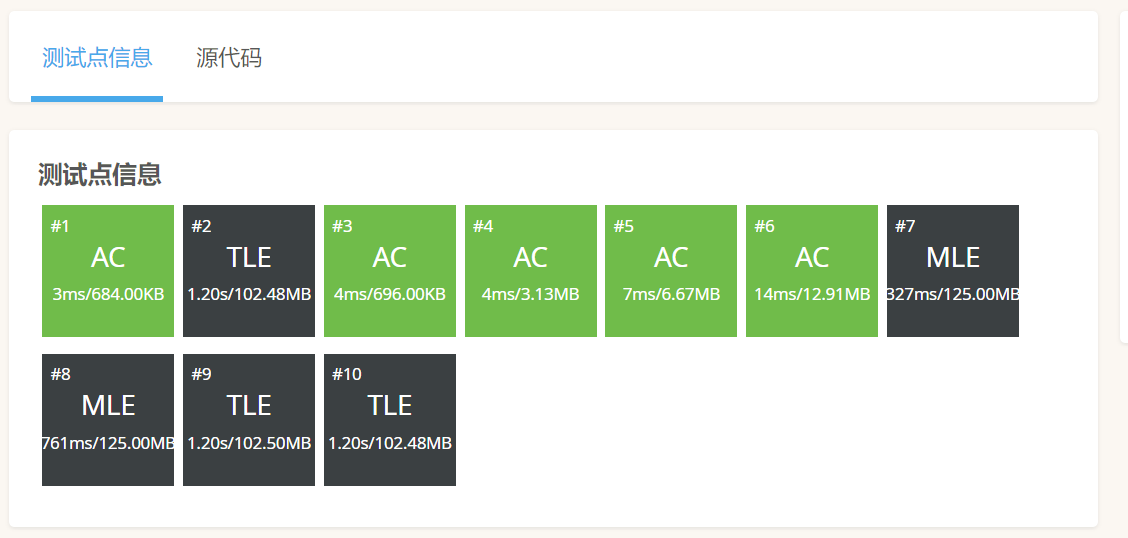
超时且超内存,我们观察本题数据范围:n最多是1e5,本题时间复杂度是O(n2) 空间复杂度也是o(n2),显然会达到1e10的时间复杂度,显然会TLE和MLE,所以我们要改进算法。
二、LCS改进至LIS(最长公共子序列改成最长上升子序列) 重要方法!
我们观察题目,可以改进成LIS,原理是:a b 数列都是 n的全排列,所以a 和 b中的元素是相同的,只是顺序不同,所以b中的每一个元素在a中都会有一个位置,所以我们把b中在a中序列的位置 构成一个新的序列c,序列c的最长上升子序列的长度,就是a 和 b的最长公共子序列的长度 :因为b的元素在a中的位置如果是递增,那么就是公共的子序列,如果不是 比如c序列:5 1 那么就说明b的第一个元素在a的第五个位置 第二个元素在a的第一个位置,那么第一个元素和第二个元素一定不会成为a 和 b的公共子序列。可以举例验证。
求最长上升子序列的方法,我们可以用二分的的方法,也是就nlogn的时间复杂度,具体可以看我 洛谷 P1020 [NOIP1999 普及组] 导弹拦截 的原理方法。
构建上述c序列的方法,我们可以创一个map数组,map下标代表a序列的每个元素值,map元素值存下标,然后map[b[i]]的值就是b的元素在a中的下标.
非常简便的一个做法。
接下来上代码:
1 //p1439 【模板】最长公共子序列 2 #include<iostream> 3 #include<cstdio> 4 #include<algorithm> 5 using namespace std; 6 const int m = 1e5; 7 int a[m], b[m], map[m], dp[m]; 8 int main() 9 { 10 int n; 11 cin >> n; 12 int len = 1; 13 for (int i = 1; i <= n; ++i)cin >> a[i], map[a[i]] = i;//map存a[i]元素的位置下标 14 for (int i = 1; i <= n; ++i)cin >> b[i]; 15 dp[1] = map[b[1]];//先初始化一个dp1 否则会错一个点 90分 16 for (int i = 2; i <= n; ++i)//二分法求最大上升子序列 17 { 18 if (map[b[i]] > dp[len]) 19 dp[++len] = map[b[i]];//dp中存的是b的每个元素在a中的下标 20 else 21 { 22 int temp = lower_bound(dp + 1, dp + 1 + len, map[b[i]]) - dp; 23 dp[temp] = map[b[i]]; 24 } 25 } 26 cout << len; 27 28 }
上结果图:时间复杂度为nlogn 大大降低



