动态规划：洛谷 P2758 编辑距离 —— 一题多解：递归和DP求解

洛谷 P2758 编辑距离

 

 这题是普及/提高－的，观察发现可以用二维数组DP做。

 

思路是建一个二维数组，dp[i][j]代表a的前i个变成b的前j个最少需要的步数。状态转移方程：

dp[i][j]=min( min (dp[i-1][j] , dp[i][j-1] )+1, dp[i-1][j-1] + flag) ;

dp[i-1][j]：表示删。表示的是前i-1个变成j的步数更少，所以不如直接删掉第i个。

dp[i][j-1]：表示增。表示的是前i个变成前j-1个步数更少，所以不如在i的后面添加一个第j个字符。

dp[i-1][j-1]:表示换。如果第i个等于第j个，那就不用换，直接dp[i][j]=dp[i-1][j-1]+flag，此时flag=1。不然就要换，就需要加一步，dp[i][j]=dp[i-1][j-1]+flag，此时flag=1。

注意点①：边界条件注意设置，dp[0][j]=j 0个字符变成j个字符要j步，dp[i][0]同理。

注意点②：因为字符串是从下标1开始，所以再创两个char数组存放数组，并让数据从下标1开始，方便后面DP计算。

 

可以有两种求解方式：DP和递归，这里的递归也可以叫做记忆化搜索。记忆化搜索一定能转化为DP，反之则不行。

一、DP

//洛谷 P2758 编辑距离
#include<iostream>
#include<cstring>
using namespace std;
char a[2002];
char b[2002];
string x1, x2;
int dp[2002][2002];
int main()
{
    cin >> x1;
    cin >> x2;
    int l1 = x1.size();
    int l2 = x2.size();
    for (int i = 0; i < l1; ++i)
    {
        a[i + 1] = x1[i];
    }
    for (int i = 0; i < l2; ++i)
    {
        b[i + 1] = x2[i];
    }
    for (int i = 1; i <= l1; ++i)dp[i][0] = i;//边界调节，b数组长度为0时，变成a数组要花i步 也就是增添i个
    for (int j = 1; j <= l2; ++j)dp[0][j] = j;
    for(int i=1;i<=l1;++i)
        for (int j = 1; j <= l2; ++j)
        {
            int flag = 1;
            if (a[i] == b[j])
            {
                //如果最后一个元素相同 那么这一步就不需要加1
                flag = 0;
            }
            dp[i][j] = min(min(dp[i - 1][j], dp[i][j - 1])+1, dp[i - 1][j - 1] + flag);
           
        }
    cout << dp[l1][l2];
    return 0;
}

 

 

二、递归

//洛谷 P2758 编辑距离
#include<iostream>
#include<cstring>
using namespace std;
char a[2002];
char b[2002];
string x1, x2;
int dp[2002][2002];
int recursion(int i, int j)//代表求a的前i个字符变成b的前j个字符需要几步
{
    if (dp[i][j] != -1)//如果已经算出来的 直接返回
        return dp[i][j];
    if (i == 0)//i等于0 需要j步 也是计算边界条件
        return j;
    if (j == 0)
        return i;
    int flag = 1;//判断最后一个字符相等不 的标志
    if (a[i] == b[j])
        flag = 0;
    return dp[i][j] = min(min(recursion(i - 1, j) + 1, recursion(i, j - 1) + 1), recursion(i - 1, j - 1) + flag);
}
int main()
{
    cin >> x1;
    cin >> x2;
    int l1 = x1.size();
    int l2 = x2.size();
    for (int i = 0; i < l1; ++i)
    {
        a[i + 1] = x1[i];
    }
    for (int i = 0; i < l2; ++i)
    {
        b[i + 1] = x2[i];
    }
    memset(dp, -1, sizeof(dp));
    int ans = recursion(l1, l2);
    cout << ans;
    return 0;
}

 

 

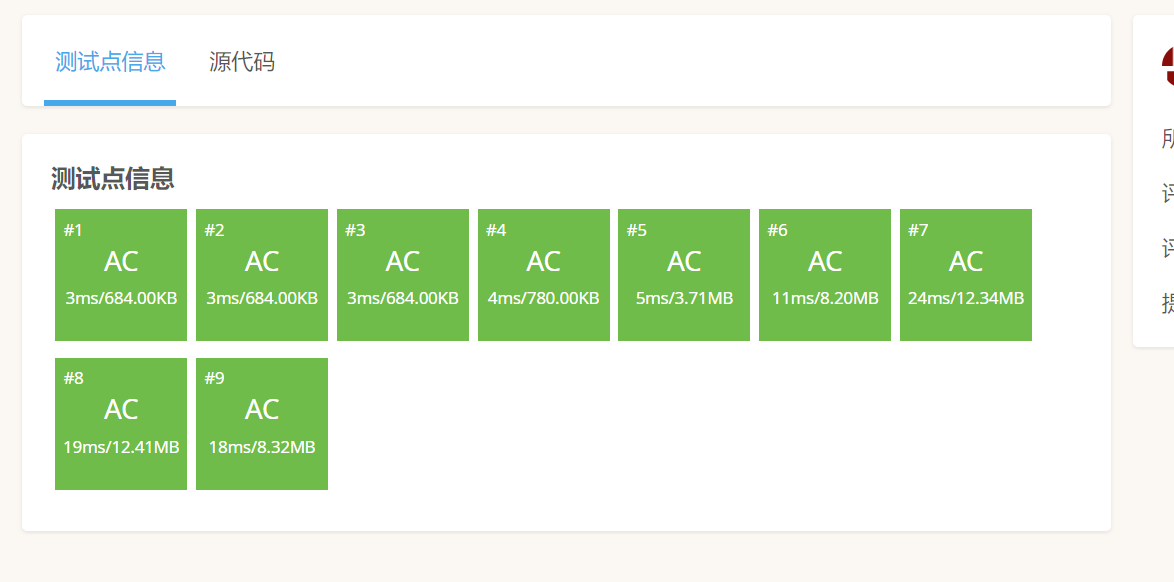
三、对比时间复杂度

DP：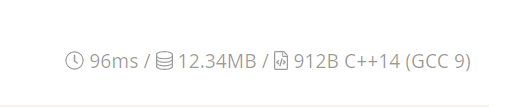

 

递归：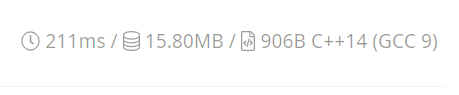

 

 

显然DP的时间复杂度更小，差了两倍多，空间复杂度也更省点。