一些题解
1.贴贴
懒得写代码了
首先有个单次询问O(n)的直接换根DP做法,枚举相遇点,略。
像这种每次找一类点计算答案的题,考虑虚树。
有个结论:相遇点选在颜色为x或y的点上 不会更劣
所以只需要在同时包含x和y色的虚树上换根DP,枚举相遇点就行了
但复杂度波动很大。当max(size x,size y)比较大时,复杂度就高;
考虑均衡一下,根号分治。maxsize<sqrtn直接暴力,预处理所有maxsize>sqrtn的对,O(n sqrt n)。(具体来说,对于每个size>sqrtn的点,在原树上换根DP。在颜色为k的点上时,就和k的虚树统计答案)
还有个小优化,每次建同时包含x色和y色的虚树时,不用按dfs重新排序,只需要把x色和y色的有序序列归并一下,这样子每次直接算答案的部分,复杂度就优化到了O(sqrt n)
O(nsqrtn+msqrtn)
2.The Tree
有几个巨佬,非常快的秒掉了。
我当时想了个定期重构的方法,但是没写。
首先感操作1不好操作,查询很好操作。考虑平衡一下,操作1直接考虑在x点打标记 w++,查询就查x到根的链。
查询时,x点为黑,当且仅当存在x的一个父亲y,满足x到y路径所经过的点数 小于路径上所有点的w之和。
初始时把每个w设置成-1,就相当于判断 x到根的路径 的所有后缀路径 的w之和 的最大值 ,是否>=0。
考虑树剖加线段树维护。
至于操作2,先把x的子树的点赋值为-1(我到现在才意识到 树剖是可以子树修改,子树查询的),再考虑减去x的祖先对子树的贡献。
如果x的祖先y影响到了x的子树,一定会向下蔓延(x到y路径的w之和)层。我们就把x的w减去(x到y路径的w之和)+1,类似于用海绵吸掉蔓延的黑色
但是假设我算答案的时候,没有取到y,但经过了x,x就会吸掉无辜的黑色,会不会有问题呢?
实际不会,显然取x一定不如取y优秀,毕竟(x到y路径的w之和)>=0,除非……有其他操作2。但是一对x到y的路径上的点 进行操作2,x的w就成-1了,也不会吸了。
时间复杂度O(nlog^2)
sto nkrqoi002
首先做这道题,要会有向完全图三元环计数。
手玩一下可以发现,三元环不太好计数,但是非三元环很好计数。对于任意三个点,只要有一个点有两个入度,这就是个非三元环。
(确定三元环需要三个点的状态,而确定非三元只需要一个点的状态)
因此 可以容斥。三元环总个数就是C n3 -∑C in[u] 2,每个三元环只会被计算一次。
得出这个美丽的式子之后,考虑如何计算答案,首先C n3是定值,对答案无影响,只剩 -∑in[u]*(in[u]-1)/2,除以2也可以提,就变成了∑in[u]-∑in[u]^2
∑in[u]值是定值 我们只用让∑in[u]^2最小。
这种选择性定向的题,比较容易想到网络流。选择费用流,s连询问点,询问点连右边原图上的点,原图上的点就1,3,5,7地往t连。
4.平均回文
枚举中心+二分哈希
每次两边同时遇到一个‘?’,概率就要除以26。多除几个26,概率就爆出精度了,直接结束循环。挺有意思
5.小w的喜糖
这题在容斥专题里,所以是容斥(而且约束条件有点怪。
F[i]表示至少有i个人与手中糖的颜色冲突 的方案数。我们只需要固定i个人冲突,其他人随便选,就可以计算f[i]。f[i]容斥一下就是最终答案了!
我们现在只需要研究固定i人冲突的方案数了
由于原题的同一颜色糖果等价,不太好处理,有一个小技巧,先把每颗糖都当做不同的,只考虑约束条件,最后求出方案数后,再按可重集排列去重(学到了!!!)。
我们考虑在每种颜色中选一些人来冲突,这不太好直接列式子,数据范围又小,直接dp。
dp[i][j]表示前i种颜色,已经选了j个冲突的人,的总方案数
转移明显就是枚举当前选几人冲突,dp[i][j]=∑C(num[i],k)*A(num[i],k)*dp[i-1][j-k] ,注意我们已经假设每颗糖不同,所以要乘A()
F[i]=f[n][i]*(n-i)! 最后容斥一下即可得到答案(别忘了去重)
看到zmz再看这道题,我就凑上去看了看,并点开了算法标签,说“太简单了,这不就是,倍增 加 trie树 加 位运算吗,秒了!”
后来我想了一下这道题,发现按trie树一想就直接出来了,trie树合并 加一个 搜11111链并交换节点左右儿子的修改,O(nlogn),看了一眼题解,可以这么写。
(之前希希好像口胡了一道题让我想,解法就是交换线段树的左右儿子,导致想这道题简单了许多)
当初不该看标签,感觉略过了这题最难的部分。
收获:trie树可以合并,+1操作可以在trie树上体现
7.https://www.luogu.com.cn/problem/P5445
这道题在CDQ作业表里,当时就一直对着CDQ想,始终想不出来,对时间分治,区间分治好像都不行,便“低头”了。
实际上是需要转化的。因为我低头了,所以我不太清楚咋想到转化,因为我真的想不到啊。
洛谷一篇blog写道:"看到点对,什么思路?转化为平面问题。显然点对连通性可以转化到平面上”
挺有道理,这种二元组,点对的题,都可能联系上矩阵(学到了!!)
总之,可以使用一个矩阵表示连通性。当联通 i-1 所在的连通块(L)和 i+1所在的连通块(R)时,给每个(l,r)和(r,l)加上q-now的值。
相对的,当删除时,给每个(l,r)和(r,l)减去q-now的值。
发现这玩意是个矩阵操作,要求矩阵加,矩阵减,单点求值。
二维线段树和CDQ都能过(实际上我一种都没写,口胡)
8.I - [WF2015 J] Tile Cutting | CQNK (nks.edu.cn)
很骚的一道题。
首先一眼感觉这玩意和询问没多大关系,应该是诈骗。我们直接不管,尝试求出每个cnt[size]
初感觉就是在矩形(或直角梯形)的基础上,加上一些变量,来唯一地确定一个平行四边形,并表示出它的面积(毕竟你看题面给你的图片,都是一个矩形框住了一个平行四边形),再从其面积的式子中找点规律。
然后我们随便设设,like this
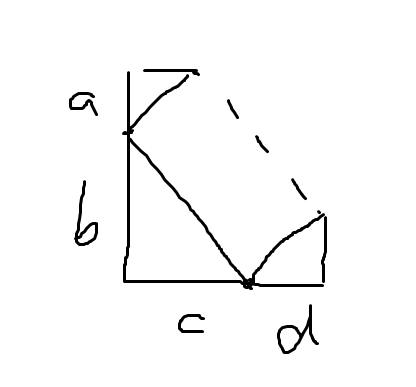
(很悲伤的是,在开这道题的时候,我还挺快地想出了以上步骤,结果我把平四面积表示错了!表示成了个6项式,直接舍弃了这种做法)
我们就会发现这玩意的面积为ad+bc!!!简直是送到嘴上的FFT (也没有很送到嘴上,因为它在FFT专题里)( Ci=∑Ai-j*Bj,这个平行四边形面积就是 i ,ad 就是 i-j,bc 就是 j)
然后就可以很舒服的用FFT搞了
最后询问随便处理处理就行,我写的st表。
M - [Tjoi2016&Heoi2016]求和 | CQNK
another 多项式乘法
首先我们直接把第二类斯特林数拆开,再约一下分,可得
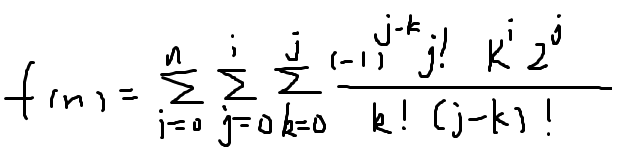
理性分析一波。右边的一坨中,分别有和 j ,j-k ,k ,(k和i)相关的项,
我们发现 j ,j-k ,k 这种处理着很舒服,只有n种值,看着就像多项式乘法 ;与 k 和 i 同时相关的项就很难受,它有n*n数量级的取值,不好搞。
但是与 i 相关的只有 k^i 这一项,我们可以考虑把 sigma i拿进去。
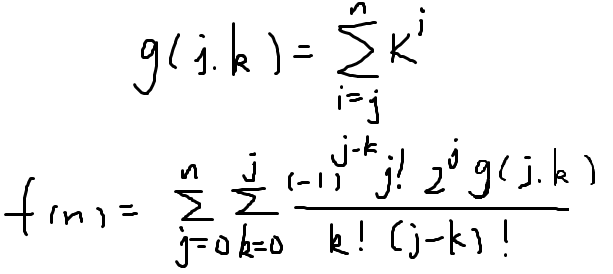
我们发现几乎搞了个寂寞,g数组也求不了,而且式子里又多了一个与 j 和 k 同时相关的项。
当时到这里就做不动了。
然后请教了一下柏霖,他说 “把 j 的上界换成 n”。我听了一脸懵,又看了一眼原式子,恍然大悟。
首先把 j > i 时肯定不影响答案
注意到如果把 j 的上界换成 n,i 与 j 就无关了。再来看 k^i ,惊讶地发现,原本需要传入 j k的 g() 只需要传入一个 k 了!!!因为 i 不再受 j 的约束了!!!
现在式子里只有和 j ,j-k ,k 相关的项,NTT O(n*logn) 解决!
这种思路可以用来去除变量间的约束,挺有用的。
你一看枚举矩形,要么枚举右下角,要么扫描线。
枚举右下角试了试,发现不太好维护某些东西;又试了试扫描线,发现有一个 ∑minn(l,r)+1-( K/len ) 的式子。枚举 l,r 显然是不行的,那就枚举值。
K/len像是可以整除分块,但是minn(l,r)就难搞了。于是咱们就搞 minn(l,r)。笛卡尔树呼之欲出,式子成了∑(minn+1-( K/len ))*sumlen,拆成∑(minn+1)*sumlen-∑( K/len )*sumlen
sumlen实际上是一个先增再不变后减函数,增减量都为+-1,∑(minn+1)*sumlen 等差数列,∑( K/len )*sumlen 预处理
场上1h想出来,1.5h都没写出来!!!
最后开始赌博,孤注一掷,发现没戏,速码暴力,暴力还CE了,光荣爆零。
哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈!!!
终于有一道纯自己过的题了
而且做法挺优秀(!!!
但是这道题还想了比较久,昨天想了1h,写了1h,调了1h。
首先很明显枚举最大的惩罚系数,再求所有方案人数之和。对第 i 人,右边随便选,左边确保其交集为空
先来个 Ei,表示有 i 个元素,选出若干子集使得它们交集为空
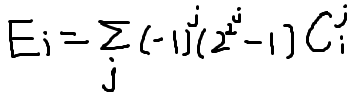
(二项式反演容斥一下可得)
再来个 Fi,表示有 i 个元素,所有选子集方案中,选出子集交集大小之和
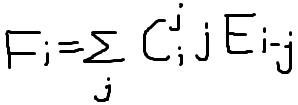
然后自以为可以统计答案了,随便写了个啥式子,发现过不了样例,调了一晚上后,我发现我的式子萎了。
大概就是我默认把 i 左边的人全部不选。没考虑到 i 左边的人也可以被选在其中一些集合中,只要不被包含再交集中就行了。
于是乎我又列了一个式子
Gi 表示 n 个人中,(前 i 个人交集为0,第 i+1 人必选,其他人随意选) 的 所有选子集方案中,选出子集交集大小之和
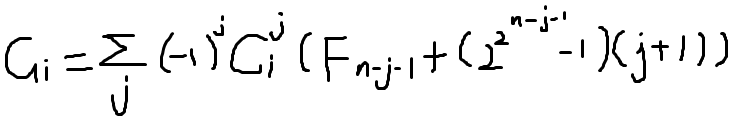
(再次二项式反演容斥)
以上三式皆可用NTT算,这个肯定就没问题了。
按照正常剧情,现在我就应该A了,但是NKOJ为这段故事填上了浓墨重彩的一笔
意思就是被卡常了。
问了一下他们,他们说他们只用了两次多项式乘法,而且还要强制 limit 为 2*n 而不是 4*n。
我尝试把上面的式子合并,发现不行。
当我拎出其中一个式子时,我发现我就是个 傻B
"再来个 Fi,表示有 i 个元素,所有选子集方案中,选出子集交集大小之和"
加入这玩意强迫你O(1)求 Fi ,咋求?
咱直接讨论 每个元素 j 有多少贡献。只有当选出所有子集都包含 j 时 它才有贡献,这不就是
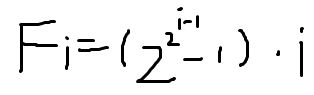
选出的每个集合都必须包含 j ,一共 2^(i-1) 个这种集合,总方案就是2^2^(i-1)-1(空集),每个元素又等价所以*i
过了
这个故事告诉我们,别学NTT学傻了(我觉得我思路也有点奇怪,正常应该先想到G的式子,再想到F的式子,鉴定为学多项式学的
很明显直接枚举 N个位置中出现次数恰好为S的颜色种数
尝试统计 N个位置中出现次数恰好为S的颜色种数为i 的方案数。发现不太好搞,考虑 N个位置中出现次数至少为S的颜色种数为i 的方案数
假设有 i 种颜色,首先有一个C(m,i),iS 个位置类似可重集排列,剩下位置的随便在(n-i)选。
但这样子还是会算重方案数,具体式子我忘了(应该长得和下图形式二差不多)。
反正得二项式反演一下。

然后就可以NTT了
论文题,学到了一些推式子思路。
根据经验,我们考虑只算出环长为 i 时第一个人的存活率,其他人的存活率就可以直接表示
设一个人死的概率为p,活的概率为q=(1-p),很容易推出一个人在前i轮死掉的概率为1-q^i;然后又可以推出 n-1人在前 i 轮全死的概率为(1-q^i)^n。
然后就可以列式子,设当前环长为n,第一个人最后死,当且仅当他在第 i 轮结束的新一轮后死掉时,剩下n-1人在i轮之内全死了。
可以列式
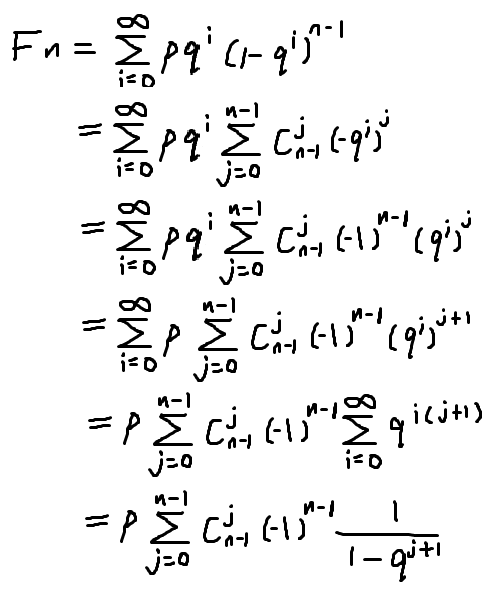
(不会latex)
然后F也可以用多项式乘法算了
这个推式子对我来说挺有启发性,建议反复观摩
4个月前场切了,今天看了1h之前的代码才看懂是怎么写的
首先我们可以想到一些暴力,比如O(1)修改, O(n)枚举子集查询;或者O(n)枚举超集修改,O(1)查询。但是都过不了
看到这修改和查询用时的不平衡,我们可以想到结合一下。
正常做法:
把一个数拆成两部分,前一半位和后一半位。然后设 f s1 s2为前一半位恰好为 s1,后一半位为 s2 的子集,的总方案数。
这样子查询就只需要枚 s1 的子集,修改就只需要枚举 s2 的超集,成功平均。
我当时的离谱做法:
把数分为 bitcount>=8(A类) 和 <8(B类) 两种
算贡献时:(当前计算的是 => 号右边的贡献)
A对A的贡献:超集修改,单点查询
B对B的贡献:单点修改,子集查询
A对B的贡献:推一下发现,A对B有贡献当且仅当 A的补集&B=0。
又有一个很神奇的性质,如果对B子集修改,对A的补集的子集查询时 对 popcount%2 进行(+-)容斥,只有当 A的补集&B=0 时,B的贡献才不会被容斥抵消
(我也不知道我当年是怎么想到的)
按照上面实现即可。
我是傻逼我是傻逼哦我是傻逼我是傻逼我是的我怕调查的2发如此肤浅如果vi哦1其他人突然发。 vbqwrtbn
有一个性质,当且仅当m在二进制下是n的子集时, C(n,m)为奇数。手玩和用拓展卢卡斯均可得到。(这是之前一道题的结论)
然后就变成了上面那道题倒过来。
如果偏要正着做,我当时的离谱做法好像就不太好推了;但是正常做法依然强劲。
所以说这题等于两道原题加起来
考场上执着于莫队,导致一直没想出正解。
实际上区间查询的题不只有莫队一种较通用的做法。
可以用数据结构,整体二分,莫队,对询问按右端点排序再挪指针 等等。
对于(是否存在某个元素)这种问题,莫队 和 排序加挪指针 比较常见。
这道题就是最后那种。
我们只需要在挪动右端点的同时,维护 当前倒数第一个 a[i] 含有某个质因子p的 i ,在树状数组中 标记一下它的贡献(p-1)/p 。O(nlogn^2)
感觉比较板的一题,估计是因为分治FFT本身就是紫题了。
很明显,这是一道概率DP,我们得先设状态 F u i ,表示当前是第 i 秒,在 u 点,到n点的最小期望。
如果将 F u 作为一个整体去转移,就会发现转移中有环。于是不得不枚举 i ,一层一层地转移
\(F_{u,i}=min_v\{\sum_{j=1}^tF_{v,j}*P(uv,j-i)\}\)
就可以O(n*t^2)地求解了。
尝试发现一些性质,最后你会发现没有性质。
首先这题似乎不太符合普通最短路的性质,有可能走回头路,比如
再猜点其他结论,什么通过某个点一条边转移的时间点是连续的,等等,会发现都不成立。
我们就把矛头指向DP方程
\(F_{u,i}=min_v\{\sum_{j=1}^tF_{v,j}*P(uv,j-i)\}\)
首先我们把总期望转化为每条边的期望之和,明显每条边被选中的概率相同,都是 \(\frac{n-1}{\frac{n*(n-1)}2}\) ,即 \(\frac2n\)
(这个可以由 \(\frac{C_S^{n-1}}{C_{S-1}^{n-2}}\) 化开得到,其中 \(S=\frac{n*(n-1)}2\);也可以理解为每条边的期望是 \(1\),最后所有边的期望之和为 \(n-1\))
\( \begin{aligned} F(n)&=\sum_{i=1}^n\sum_{j=i+1}^n(i+j)^m\\ &=\sum_{i=1}^n\sum_{j=2*i+1}^{i+n}j^m\\ &=\sum_{i=1}^nS(i+n)-S(2*i)\\ &=\sum_{i=1}^nS(i+n)-\sum_{i=1}^nS(2*i) \end{aligned} \)
拉格朗日插一下\(F(n)\)即可
最后别忘乘 \(\frac2n\)
Ⓑ - 【SAM】子串的价值
很琴瑟的一道题
首先,子串长度*出现次数 = 后缀自动机
所有直接上SAM!!!\(O(n)\)
对于第一问,由于我们无法一次存下所有价值,所以只能二分答案ans(这玩意明显有单调性),然后判断价值>=ans 的子串有没有m个(这部分在自动机上做,\(O(n)\)),一共 \(O(n*logn)\) 。
二分出ans后,直接把 价值>=ans 的子串的价值 全部取出来排序即可,\(O(n*logn)\)
(这里有一个小问题,如何保证价值>=ans 的子串的数量?首先价值>ans的子串的数量不超过m;其次价值=ans 的子串的数量也是 \(O(n)\) 级别:对于自动机上每个点所表示的子串,至多只有一个价值=ans)(或者你也可以直接把 价值>ans 的子串的价值 取出来排序,剩下的全用ans补上)
对于第二问,我们采用与第一问相似的思想:先二分答案算出第k小的子串的价值ans,再让 k-=(价值小于ans的子串数量)最后对 价值=ans的子串 ,找出第k小。
一种方法是排序,使用哈希,存子串只需要存它在原串中的pos,根据上面的证明,这是 \(O(n*log^2n)\)的;这道题又只需要求第k大,所以可以使用nth_element,\(O(n*logn)\)
当然还有更优秀的方法:
我们充分利用fail树的性质:每个节点所代表的子串 是 其子树内所有节点所代表的子串 的后缀
那我们 reverse 一下再建树,则,每个节点所代表的子串 是 其子树内所有节点所代表的子串 的前缀
说明每个节点所代表的子串 比 其子树内所有节点所代表的子串 字典序小。
那我们就可以预处理子树内 价值=ans的子串 个数和,最后按字典序在fail树上随便跑跑就完了
(另一个小问题,要想在fail树上从上往下跑,我们需要把它改造成 类trie树,如图)

(边权为,son代表子串的从后往前数的第len[father]+1个字符)
(具体怎么存子串?还是存 其在原串上的pos)
总结:其实这道题并不难想,二分答案之类的呼之欲出。只不过是想介绍一下存pos,fail树转trie树之类的思想。可以说是为了这盘醋包了顿饺子。


