暑假小总结

暑假的基科班从6号开始上，上到22号，三周时间学的很多，难度也很高。本人是全班最菜，所以很多知识都不太会，而且写题也写得很慢，不过勉勉强强跟上。

第一波训练已经结束了，浅浅总结一下学了些啥

 

数据结构：

1.笛卡尔树：

一种二叉搜索树，满足堆的性质。

可以这样理解，一个序列对应到一棵树上，使原序列的每段连续区间 对应 树的一棵子树 。

其中，这段区间的最值就是子树的根，区间被最值分成的左右两部分 的最值 分别是 根的左右儿子。

所以对于笛卡尔树 左儿子在序列上的位置（下标）< 根的位置< 右儿子的位置

一个图辅助理解（min为区间最小值）

没有重复数字的话，笛卡尔树唯一。

建树：O（n），开一个单调栈进行建树。按照序列的顺序从左往右，加入每一个值。

单调栈存 从当前树根一直往右的链，加入下一个数，一定会作为链上某个节点 的右儿子（如果不是，则插入的位置不满足为所有子树的右儿子，必定在之前某一节点的左子树下，不符合笛卡尔树（左儿子在序列上的位置（下标）< 根的位置））

然后又因为父小子大，就不停弹栈找第一个比自己小的父亲，再作为它的右儿子。

至于弹掉的链，就接在本节点的左子树下，作为左儿子，。

有什么用？

可以找a[i]作为最小值的区间，也就是a[i]为根的子树对应的原序列区间

针对于某些题目，可以使用笛卡尔树求区间最值。（但这个最值不是像st表随便求，是对于被最值划分的区间求最值）

 

2.莫队（不知道算不算）

离线算法，处理区间询问，时间O（N*sqrt（N））（基础莫队）

对于提出的许多区间询问，考虑开l，r两个变量，表示目前区间的左右端点。当询问到L，R区间时，移动l，r端点并对需要统计的答案进行更新。时间O（mn）

考虑到l和r来来回回移动太重复太慢，可以想到将询问的Li，Ri排序。但如果只是普通的双关键字排序，那么无论对l还是r排序，另一方都是趋于无序的，没用。

所以就想到将原序列分块，将L所在的块作为第一关键字，R作为第二关键字排序。对于l，在块内每次移动O（sqrt(n）），跨块的移动总共O(n），总共O（m*sqrt（n））；对于R，当L在同一块中，最多扫一边序列，O（n），而L一共会跨sqrt（n）块，总共O（n*sqrt（n））。合起来就是O（（n+m）*sqrt（n））

在使用莫队时，为了保证时间复杂度，必须做到O（1）移动l，r；移动完l，r后，最多sqrt（n）统计答案。

 

树上也可以跑莫队，要用欧拉序跑（dfs序太抽象了，跑不动），用那个记录 第一次和最后一次经过某一点的时间 的欧拉序。然后就和序列跑莫队一样了；

 

还有一个小技巧，可更改莫队（三关键字），就是在询问L，R的同时加上更改操作，将a[i]改成x。

也很简单，加上一个T时间戳即可，表示此次询问操作前有T次更改。每次将l，r更新完后，再更新当前时间now到 询问的时间。

这时候排序要改为根据Li，Ri所在的块号与T的大小排序。

时间复杂度 n^(5/3) (n的三分之五次方），块长设成n^(2/3）感兴趣可以自己证

3.李超树

用线段树维护x轴。对于线段树的每一个节点，有l，r表示维护的区间。设l，r中点为mid，维护一个h，表示所有线段中 与直线x=mid的相交的位置最高的线段。

对于每一条线段，算出它的斜率k和截距b，在线段树上的x0~x1区间进行修改。

如果x0~x1区间还不覆盖当前节点的区间，像正常区间dp一样下放。如果覆盖：

若该点没更新过h，直接将h改为本线段。

如果该区间已经有标记了，由于标记难以合并，只能把标记下传。但是子节点也有自己的标记，也可能产生冲突，所以我们要递归下传标记。

 

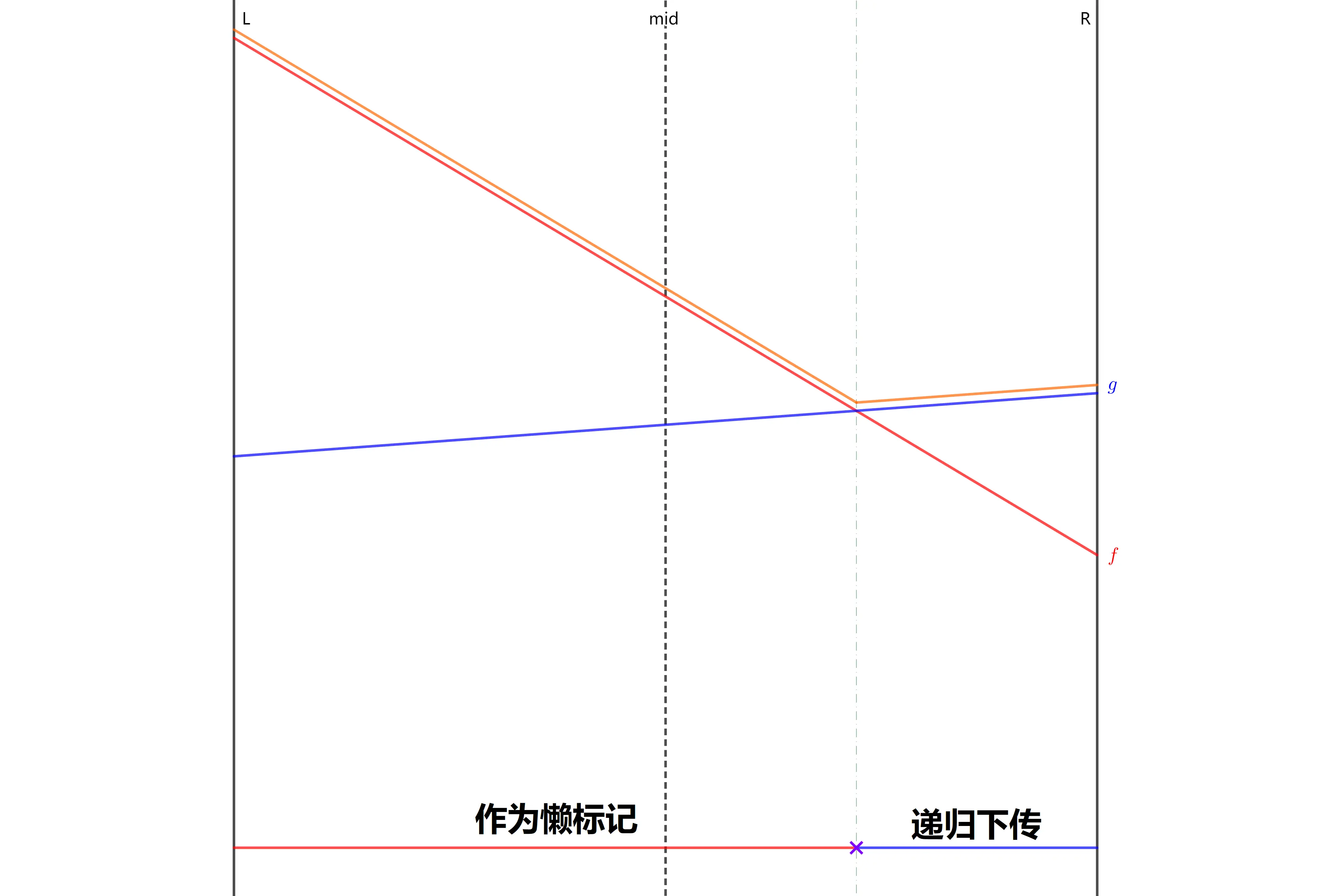
如图，按新线段 是否大于原线段 ，我们可以把当前区间分为两个子区间。其中 肯定有一个子区间被左区间或右区间完全包含，也就是说，在两条线段中，肯定有一条线段，只可能成为左区间的答案，或者只可能成为右区间的答案。我们用这条线段递归更新对应子树，用另一条线段作为本区间的h（摘自oi.wiki）

这个修改其实是logn*logn的，x0~x1最多覆盖logn段，被覆盖每一段的又最多会更新其子树内logn个点（线段树深度logn），但是实际上跑不满，还很快。

 

查询时，我们可以利用标记永久化思想，在包含k的所有线段树区间（不超过nlogn 个）的标记线段中，比较得出最终答案（摘自oi.wiki）

 

这玩意可以加速一些东西，比如凡是可以转化成dp[i]=max(k[j]*a[i]+b[j])这种形式的状转，都可以用这李超树搞。

4.可并堆（左偏树，斜堆都是可并堆）

左偏树：1.是一棵二叉树 2.满足堆的性质 3.定义每个子节点个数<2的节点为外节点，每个节点到达 子树内的外节点 的距离叫空距，左偏树满足左儿子空距<=右儿子空距。很明显，每个节点空距等于右儿子空距+1。（空节点，也就是不存在的节点的空距为-1，这样外节点的空距就为0了）

斜堆：左偏树去掉第3个性质

 

左偏树与并查集一起食用，效果更佳。用i在并查集中的祖先 get_father（i）表示i所在堆的堆顶.

 

可并堆，怎么合并两个堆？把一个堆的所有元素全部弹出，又放到另一个堆里？太慢了！直接log解决！

　　考虑递归合并，对于合并AB两棵子树

　　左偏树：1.找到根较大的子树 ，假设它是A

　　　　　　2.将B和A的右子树合并

　　　　　　3.更新A的右儿子，更新并查集右儿子的父亲

　　　　　　4.如果不满足左儿子空距>右儿子空距，交换左右儿子

　　　　　　5.更新根节点空距=右儿子空距+1

　　　　　　结束条件：A或B为空树

　　　　　　O（logn）

　　斜堆：管tm什么空距，直接换左右儿子。每次合并完右子树都换一次左右儿子，根节点空距也不更新。

　　　　　　网上有证明这玩意均摊不过O(4logn)，有兴趣自己去搜。

怎么删堆顶？

1.合并堆顶x的左右儿子，设新堆顶为top

2.修改并查集。断绝父子关系：father[top]=top,father[x]=top（之前的那些子孙都指向x，通过改father[x]让他们指向新top（这时候如果要将x加入另一个堆，直接加不了，不然会影响在之前指向x的子孙，得另外给x开一个点再加））,ls[x]=0,rs[x]=0;

 怎么加点？

合并堆和一个点

 

图论：

1.最短路，最小生成树，拓扑序复习；次小生成树

次小生成树：先建最小生成树，再去枚举没用来建最小生成树的边。一条没用来建最小生成树的边的  俩端点u，v，在最小生成树上的路径，与这条没用来建最小生成树的边构成环，可以在环上任意删一条边。要想次小生成树，就在最小生成树u，v路径上找最大的边（倍增lca找路径时顺便求一下）删去，再加上这点没用来建最小生成树的边，最后在所有方案中求min。O（mlogn）；

2.连通性专题（边双，桥，点双，割点，圆方树，强连通），tarjan算法，有向图缩环

 

考试：

1.组队赛（with鸟人）

这场我先开的T2，鸟人做T1，大概30min我A了T2，鸟人T1Wa85，然后他调了一个小时A，我看后面的题也没想出来。后来我帮看了看T1，他A了T3，T4打了12分，最后312.

这场考试是队里的第一次考试，我只能说稳扎稳打A了T1T2；T3需要使用随机化算法，这种套路我没有接触过；T4构造题，脑子不够用。

这场考试说明了组队赛分工的重要性，也让我认识到我还需要 在做题中多多学习总结套路和经验

2.组队赛（with luomiao）

这场我先把A~D都看了一遍，结果一道题没思路，luomiaoA了A后去开了B，我看榜单上他们把F和H做了，我就去开。当天状态一般，前一个半小时啥题都没出，后面把H出了。最后也只A了两道。

这场考试我俩没怎么交流，导致开题有些冲突，加上难度本身偏高，成绩不好。

ICPC的赛题太多了，难度也不一定递增，需要合理安排开题顺序，而且及时前面题没思路，也不要慌，冷静的去开下一题。

3.周赛一

这场T1构造，T2图论，T3DP，T4生成树

构造我想了一个小时，但是在最后写的时侯脑子抽风了，导致思路对了，代码0分。T2本来是要怎么找环的，我直接一个spfa骗80。T3DP不太擅长，骗了点分。T4本来也是骗分的，结果最后写完了没运行就交了，CE0.

这场T1 0分就很惨，应该打个SPJ，这道题SPJ也不难。T4真的太不应该了，如果检查一下是可以得40分的。

总而言之，写完码一定要好好检查，不要本该A的题爆0。

4.练习赛

T1T2T3图论，T4T5莫队

T1根本不太会，随便骗了27；T2想到了树剖，但是写挂了，只有40分；T3是最短路，也可以用最小生成树，这道题有一道简单版，我没做过，导致这道题也不会；T4莫队，我没想到n^7/4可以过，也没想到nsqrtn的正解，暴力50分；T5没想到可以使用根号分治，暴力50；