上台阶问题

面试题：一个小朋友吃n颗豆子，每次只能吃 1 个或者 2个， 但不能连续吃两个，有多少种方式吃完N颗豆子

joliya

一个勤恳没有收入的码农

 

 

不知道有没有同学遇到过这个题目，或者说类似的。

如果leetcode 刷的多的同学或者对算法敏感的同学，一下子就能想到这个题目的一种解法——动态规划。

这个题目属于 典型的 上台阶的问题（leetcode：

力扣​leetcode-cn.com/problems/qing-wa-tiao-tai-jie-wen-ti-lcof/

）

那么这个题目和 上台阶问题有什么不同呢？ 本题多了一个限制条件， “不能连续吃两个”。

先分析，要吃到最后一颗豆子，最后一次吃 要么是 剩一个，要么剩两个。

剩余 n-1 颗豆子的 吃法： f(n-1)

剩余n-2 颗豆子的 吃法：f(n-2)

但是由于不能连续吃两颗豆子。故 最后一次吃两个的话， 倒数第二次只能吃一个。所以 实际上 f(n-2)的吃法是 f(n-3)

简单画图 示意一下：

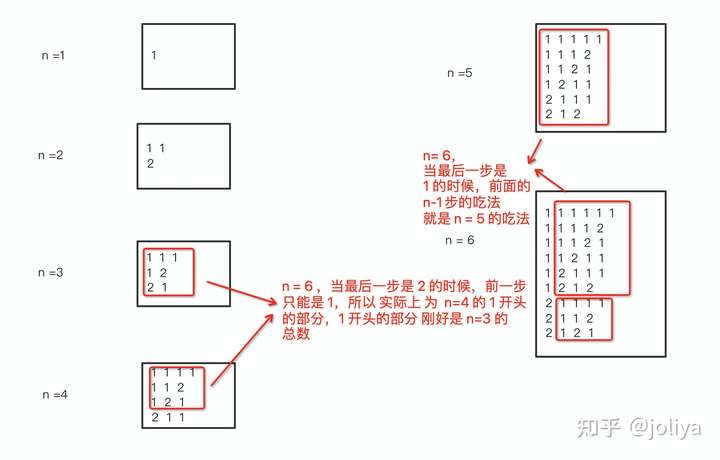
最终的状态转移方程是 f(n) = f(n-1) + f(n-3)

附上python 代码

    if n < 5:
        return n
    f = [0] * (n + 1)
    for i in range(5):
        f[i] = i
    for i in range(5, n+1):
        f[i] = f[i-1] + f[i-3]
    return f[-1]