2020 牛客多校第二场 ABCDFGJ
2020牛客暑期多校训练营(第二场)
A、All with Pairs
题意
给你 \(n\)个字符串\(s_1,s_2,\ldots ,s_n\) ,\(f(s,t)\)为找到最长的\(s_{1\ldots i} = t_{|t|-i+1\ldots |t|}\),就是找最长的字符串\(s\)的前缀等于字符串\(t\)的后缀,问\(\sum_{i=1}^n\sum_{j=1}^nf(s_i,s_j)^2\pmod{998244353}\)
思路
-
判断一段字符串相等,可以把字符串转换成\(hash\),存储起来。
-
那么就把所有后缀都转换成\(hash\)存起来,然后遍历每个前缀的贡献
-
但是直接算当前前缀的贡献会出现重复计算贡献的情况,因为要求最长的前缀等于后缀
比如\(abca\), 如果能在\(abca\)匹配到,那在\(a\)就一定也匹配到过,那么应该怎么去重
-
然而\(kmp\)算法中的求\(next\)数组就可以很好的解决这个问题。
\(i\):当前匹配到该元素的第\(i\)位
\(now\):当前的\(hash\)值
\(mp[now]\):表示\(hash\)为\(now\)的后缀的个数
\(ans = mp[now] * ( i * i - (nxt[i]-1) * (nxt[i]-1));\) 当前的贡献
代码
#include<bits/stdc++.h>
#define pb push_back
#define mes(a, b) memset(a, b, sizeof a)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const ll mod = 998244353;
const int maxn = 1e6+10;
const double eps = 1e-9;
const ll inf = 1e18;
const ull seed = 13331;
int T;
int n, m;
string s[maxn];
map<ull, ull> mp; //记录后缀Hash值的个数
int nxt[maxn];
void getNxt(string str){ //求next数组
int len = str.length();
for(int i = 0; i <= len; i++)
nxt[i] = 0;
int i = 1, j = 0;
nxt[0] = -1;
while(i < len){
if(j == -1 || str[i] == str[j]) nxt[++i] = ++j;
else j = nxt[j];
}
/*for(int i = 0; i <= len; i++)
printf("%d ", nxt[i]);
puts("");*/
}
int main(){
cin>>n;
ull now, pre;
ll ans = 0;
for(int i =1; i <=n; i++){
cin>>s[i];
now = 0; pre = 1;
for(int j = s[i].length()-1; j >= 0; j--){
now += pre * s[i][j]; //计算后缀的Hash值
pre *= seed;
mp[now]++;
}
}
ll tmp;
for(int i = 1; i <= n; i++){
getNxt(s[i]);
now = 0;
for(int j = 0; j < s[i].length(); j++){
now = now * seed + s[i][j]; //当前前缀Hash值
tmp = nxt[j+1];
ans += mp[now] * (j+1) % mod *(j+1) % mod; //因为从0开始遍历,贡献要j+1
ans -= mp[now] * tmp % mod * tmp% mod; //有mp[now]会重复计算
ans = (ans% mod + mod)% mod;
}
}
printf("%lld\n", ans);
return 0;
}
B、Boundary
题意
给你\(n\)个点,找出一个圆,使得\((0, 0)\)要在圆上,并且使得最多的点在圆上,输出在圆上的点的个数。(给的点不会重复且没有原点)
(不知道是不是代码的问题,改了很多版本都差不多,但是精度一直在出问题)
思路
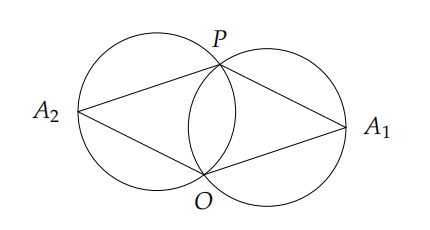
(1)同心圆的所对的夹角相等,那么固定一个点\(P\)去枚举其它点\(A\),求出出现最多\(\angle{OAP}\)的个数+1,则为答案。
(2)任取两个点\(A,B\)求出\(\triangle{OAB}\)的外接圆的圆心,排序,找出出现最多次数的圆心次数\(ans\)。设有\(x\)个点在圆上 , 则\(C_x^2 = ans\)。
代码
只写了方案一
#include<bits/stdc++.h>
#define pb push_back
#define mes(a, b) memset(a, b, sizeof a)
using namespace std;
typedef long long ll;
const ll mod = 1e9+7;
const int maxn = 1e6+10;
const double eps = 1e-9;
const ll inf = 1e18;
int T;
int n, m;
double x[maxn], y[maxn];
vector<double> vec;
int main(){
scanf("%d", &n);
for(int i =1; i <= n; i++){
scanf("%lf%lf", &x[i], &y[i]);
}
int ans = 1;
for(int i = 1; i <= n; i++){
vec.clear();
for(int j = 1 ; j <= n; j++){
if(x[i]*y[j] - x[j]*y[i] >= 0) continue;
double a = sqrt(x[i] * x[i] + y[i] * y[i]);
double b = sqrt((x[i]-x[j])*(x[i]-x[j]) + (y[i]-y[j])*(y[i]-y[j]));
double c = sqrt(x[j] * x[j] + y[j] * y[j]);
double A = (b*b+c*c-a*a)/(2.0*b*c);
vec.pb(A);
}
sort(vec.begin(), vec.end());
int num = 1, len = vec.size();
for(int i = 1; i < len; i++){
if(abs(vec[i] - vec[i-1]) < 1e-13) //精度要设置大一些
num++;
else
num = 1;
ans = max(ans, num+1);
}
if(len) ans = max(ans, 2);
}
printf("%d\n", ans);
return 0;
}
C、Cover the Tree
题意
给你一棵树,让你选择最少的链覆盖整棵树的每条边。
思路
- 链的两端尽可能的选叶子节点是最优的,那么最少的链数则为\((num+1)/2\)(\(num\)叶子节点个数)
- 根据\(dfs\)序遍历,把叶子节点存入数组,把前\(\frac{2}{num}\)个叶子节点和后\(\frac{2}{num}\)个叶子节点一一匹配。
- 具体证明,个人觉得可以贪心的思想来看,就是尽量把相邻的分开,那么就能够尽量的遍历到父节点之间的边。
代码
#include<bits/stdc++.h>
#define pb push_back
#define mes(a, b) memset(a, b, sizeof a)
using namespace std;
typedef long long ll;
const ll mod = 1e9+7;
const int maxn = 1e6+10;
const double eps = 1e-9;
const ll inf = 1e18;
int T;
int n, m;
int in[maxn];
vector<int> e[maxn], vec;
void dfs(int u, int fa){
int flag = 0;
for(auto v: e[u]){
if(v == fa) continue;
flag = 1;
dfs(v, u);
}
if(!flag) vec.pb(u);
}
int main(){
int x, y;
scanf("%d", &n);
for(int i = 1; i < n; i++){
scanf("%d%d", &x, &y);
e[x].pb(y);
e[y].pb(x);
in[x]++; in[y]++;
}
if(n == 2){
printf("1\n1 2\n");
return 0;
}
for(int i = 1; i<= n; i++){
if(in[i] > 1){ //找一个非叶子节点为根
dfs(i, i);
break;
}
}
int ans = vec.size();
printf("%d\n", (ans+1)/2);
int tmp = ans/2;
for(int i = 0; i < (ans+1)/2; i++)
printf("%d %d\n", vec[i], vec[i+tmp]);
return 0;
}
D、Duration
题意
给你一天之内的两个时间,问两个时间相差多少秒
思路
两个时间转换成秒,相减取\(abs\)。
代码
#include<bits/stdc++.h>
#define pb push_back
#define mes(a, b) memset(a, b, sizeof a)
using namespace std;
typedef long long ll;
const ll mod = 1e9+7;
const int maxn = 1e6+10;
const double eps = 1e-9;
const ll inf = 1e18;
int T;
int n, m;
int a, b, c, d, e, f;
int main(){
scanf("%d:%d:%d%d:%d:%d", &a, &b, &c,&d, &e, &f);
int x = c + b * 60 + a * 60 * 60;
int y = f + e * 60 + d * 60 * 60;
printf("%d\n", abs(y-x));
return 0;
}
F、Fake Maxpooling
题意
给你一个\(n*m\)的矩阵,\(a[i][j] = lcm(i, j)\), 问每个\(k*k\)的子矩阵最大元素的和为多少。
思路
(1)\(O(nm)\)
- 类似素数筛的方法去给数组赋值
- 单调队列维护最大值
(2)\(O(nm\log{nm})\)
- 可以用库里\(\ \_\_gcd\) 函数, (感觉比手写快很多)
- 可以用类似\(RMQ\)二维维护最大值
以上(2)二选其一可以过的,两个都用我就不知道了,(说不定扣扣就能过)。
代码
赛场中写的,单调队列写的又麻烦又慢,可以看大佬的代码(大佬的代码非常优雅)
#include<bits/stdc++.h>
#define pb push_back
#define mes(a, b) memset(a, b, sizeof a)
using namespace std;
typedef long long ll;
const ll mod = 1e9+7;
const int maxn = 5e3+10;
const double eps = 1e-9;
const ll inf = 1e18;
int T;
int n, m, k;
int a[maxn][maxn], q[maxn][maxn], Q[maxn], l[maxn], r[maxn], L, R;
//q[i]维护每行当前从大到小,且区间符合的单调队列
void add(int x, int y){ //添加第i行第j个元素
while(l[x] <= r[x] && a[x][q[x][r[x]]] <= a[x][y]) r[x]--;
while(l[x] <= r[x] && q[x][l[x]] < y-k+1) l[x]++;
r[x]++;
q[x][r[x]] = y;
}
int main(){
scanf("%d%d%d",&n, &m, &k);
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){ //手写gcd,场上超时了
a[i][j] = i*j/__gcd(i, j);
}
l[i] = 1;
}
for(int i = 1; i <= n; i++){
for(int j = 1; j < k; j++){
add(i, j);
}
}
ll ans = 0;
for(int j = k; j <= m; j++){
L = 1; R = 0;
for(int i = 1; i < k; i++){
add(i, j);
while(L <= R && a[Q[R]][q[Q[R]][l[Q[R]]]] <= a[i][q[i][l[i]]]) R--;
R++; Q[R] = i;
}
for(int i = k; i <= n; i++){
add(i, j);
while(L <= R && a[Q[R]][q[Q[R]][l[Q[R]]]] <= a[i][q[i][l[i]]]) R--;
while(L <= R && Q[L] < i-k+1) L++;
R++; Q[R] = i;
ans += a[Q[L]][q[Q[L]][l[Q[L]]]]*1ll;
}
}
printf("%lld\n", ans);
}
G、Greater and Greater
题意
给你一个长度分别为\(n, m\)的数组\(A, B\), 问数组\(A\)存在多少个长度为\(m\)的子区间\(S\),使得\(\forall i \in \{1, 2\ldots, m\} \ S_i > B_i\)
思路
(有点讲不清楚,主要是讲代码)
- 排序\(B\)数组
- 用\(bitset\)数组\(bs[i]\)记录\(B\)数组前\(i\)小的位置
bitset<mx> bs[mx];
bool cmp(int x, int y){
return B[x] < B[y];
}
for(int i = 1; i <= m; i++) id[i] = i;
sort(id+1, id+m+1, cmp); //id根据b数组排序
for(int i = 1; i <= m; i++){
bs[i] = bs[i-1];
bs[i].set(id[i]); //bs为1的位置,就是前i小的元素
}
- 通过二分查找每个\(A[i]\) 有哪些\(B[j]\)小于自己
int get(int x){
int l = 1, r = m, mid, ans = 0;
while(l <= r){
mid = l+r>>1;
if(x >= B[id[mid]]){
ans = mid;
l = mid+1;
}
else
r = mid-1;
}
return ans;
}
bs[get(A[i])] //bs中为1的位置的B元素小于A[i]
- 用一个\(res\)记录, \(res[j]\)表示当前\(\forall k \in [j, m], A[i+k - 1] >B[k]\), 如果\(res[1] = 1\),则表示整个区间都符合
bitset<mx> res;
int ans = 0;
for(int i = n; i >= 1; i--){ //从后往前遍历
res >>= 1; //把前面符合往后移
res &= bs[get(a[i])]; // bs[get(a[i])] 中有为0的位置,那么在a[i]在这个位置则不符合
if(a[i] >= b[m]) res.set(m); //当前位大于,则直接赋值
ans += res[1];
}
通过\(\&\)运算,只要中间出现0,那么这个位置之后肯定不行,手动模拟一下就比较清楚了。
代码
#include<bits/stdc++.h>
#define pb push_back
#define mes(a, b) memset(a, b, sizeof a)
#define fi first
#define se second
using namespace std;
typedef long long ll;
const ll mod = 1e9+7;
const int maxn = 2e5+10;
const int mx = 4e4+10;
const double eps = 1e-9;
const ll inf = 1e18;
int T;
int n, m;
int a[maxn], b[maxn], id[maxn];
bitset<mx> bs[mx], res;
bool cmp(int x, int y){
return b[x] < b[y];
}
int get(int x){
int l = 1, r = m, mid, ans = 0;
while(l <= r){
mid = l+r>>1;
if(x >= b[id[mid]]){
ans = mid;
l = mid+1;
}
else
r = mid-1;
}
return ans;
}
int main(){
scanf("%d%d", &n,&m);
for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
for(int i = 1; i <= m; i++) scanf("%d", &b[i]), id[i] = i;
sort(id+1, id+m+1, cmp);
for(int i = 1; i <= m; i++){
bs[i] = bs[i-1];
bs[i].set(id[i]);
}
int ans = 0;
for(int i = n; i >= 1; i--){
res >>= 1;
res &= bs[get(a[i])];
if(a[i] >= b[m]) res.set(m);
ans += res[1];
}
printf("%d\n", ans);
return 0;
}
J、Just Shuffle
题意
把一个排列\(\{1, 2, ..., n\}\) 经过\(k\)次\(B\)置换变成数组\(A\), 现在给你数组\(A\)和次数\(k\),求排列\(\{1, 2, ..., n\}\)经过一次\(B\)置换之后的数组\(a\)。
思路
(1) 我们可以把根据置换变成多个环,那么一个环同一个置换,置换\(len\)(环的长度)次为一个循环,我们知道置换\(k\)次之后的状态,那么我们找到一个\(x * k \% len = 1\)就可以求出数组\(a\)。
(2)\(x = \frac{1}{k} \pmod{len}\),求x有两种方法
- 遍历\(1\le x \le len\),找到\(x*k\%len= 1\)
- \(x * k - y * len = 1 ,exgcd(k, len, x, y) , x = (x+len)\%len\)
代码
#include<bits/stdc++.h>
#define pb push_back
#define mes(a, b) memset(a, b, sizeof a)
using namespace std;
typedef long long ll;
const ll mod = 23333;
const int maxn = 2e6+10;
const double eps = 1e-9;
const ll inf = 1e18;
int T;
int n, k;
ll exgcd(ll a, ll b, ll &x, ll &y){
if(b == 0){
x = 1; y = 0;
return a;
}
else{
ll ans = exgcd(b, a%b, x, y);
ll tmp = x - a/b *y;
x = y; y = tmp;
return ans;
}
}
int a[maxn], b[maxn], c[maxn];
vector<int> vec;
int main(){
scanf("%d%d", &n, &k);
for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
int now;
for(int i = 1; i <= n; i++){
if(!b[i]){
vec.clear();
now = i;
while(!b[now]){
vec.pb(a[now]);
b[now] = 1;
now = a[now];
}
// 循环遍历
ll len = vec.size(), inv;
for(ll j = 1; j < len; j++){
if(j * k % len == 1){
inv = j; break;
}
}
for(int j = 0; j < len; j++)
c[vec[j]] = vec[(j+inv)%len];
/* exgcd
ll len = vec.size(), x, y;
exgcd(k, len, x, y);
x = (x + len)%len;
for(int j = 0; j < len; j++)
c[vec[j]] = vec[(x+j)%len];
*/
}
}
for(int i = 1; i <= n; i++){
printf("%d ", c[i]);
}
puts("");
return 0;
}


