(1, 1)到（n, m）的方案数构造

原地址

构造\(RDB\)迷宫，要求方案数整好等于给定的\(k\)，可以构造一个二进制编码器，斜对角线上的方案数恰好是\(1,2,3,4,8,16,32...\)，用二进制可以拼出所有的数字，所以一定能造的出来。
\(B:\)可以向右或者向下走， \(R:\)可以向右走， \(D:\)可以向下走

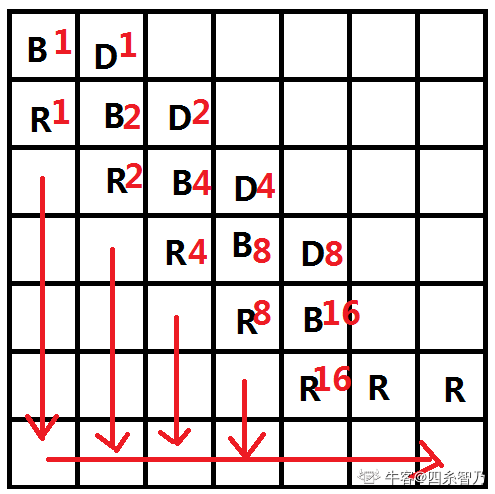
如图所示，斜对角线的\(R\)对应位置是二进制数，然后只要这一位有的话就可以直接把他变成\(B\)。
（感觉真的妙呀，听说是计组的知识，但是没学好）

题目链接

#include<bits/stdc++.h>
#define mes(a, b) memset(a, b, sizeof a)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const ll mod = 1e9+7;
const int maxn = 2e5+10;
const ll inf = 0x3f3f3f3f;
ll n;
char ch[55][55];
int main(){
    scanf("%lld", &n);
    n %= mod;
    for(int i = 1; i <= 40; i++){
        for(int j = 1; j <= 40; j++){
            ch[i][j] = 'R';
        }
        ch[i][41]='\0';
    }
    for(int i = 1; i < 35; i++){
        ch[i][i] = 'B';
        ch[i+1][i] = 'R';
        ch[i][i+1] = 'D';
    }

    for(ll i = 0; i < 35; i++){
        if(n & (1ll<<i)){
            ch[i+2][i+1] = 'B';
            for(int j = i+3; j < 40; j++){
                ch[j][i+1] = 'D';
            }
        }
    }
    printf("40 40\n");
    for(int i = 1; i <= 40; i++)
        printf("%s\n", ch[i]+1);
    return 0;
}