数学结论、计算几何
排列组合


圆排列
有限多重集的排列 n!/(n1!*n2!*...*nk!)
n元无限集可重-r组合C(n+r-1,r)种。
n元无限集取r个,n中每个至少出现一次C(r-1,n-1)(r≥n)
直线分平面:
f(1) = 2
f(n) = f(n-1)+n = n(n+1)/2+1
折线分平面:
f(1) = 2
f(n) = f(n-1)+4(n-1)+1 = 2n^2-n+1
圆分平面:
f(1) = 2
f(n) = f(n-1)+2(n-1) = n^2-n+2
三角形分平面:
f(1) = 2
f(n) = f(n-1)+6*(n-1)
平面分空间:
f(1) = 2
g(n) = n(n+1)/2+1
f(n) = f(n-1)+g(n-1) = (n^3+5n)/6+1
已知p1(x1,x1),p2(x2,y2),求Ax+By+C = 0
A = y2 - y1
B = x1 - x2
C = x2*y1-x1*y2
海伦公式
四边形最大面积
斯特林公式:
n很大时,![n! \approx \sqrt{2\pi n}\, \left(\frac{n}{e}\right)^{n}.]()
笛卡尔定理
4个圆相切,外切k = 1/r,内切k = -1/r,圆退化成直线k = 0。


一个长度为n-2的Purfer序列唯一对应一个n个点的树,且Purfer序列中i出现的次数就是节点i的度数减一。
全面积为πa2的圆锥最大面积为sqrt(2)/12*πa^3。
正弦定理sinA / a = sinB / b = sinC/c
余弦定理a² = b² + c²- 2bc·cosA
正切定理(a+b)/(a-b) = tan[(A+B)/2]/tan[(A-B)/2]
多边形面积 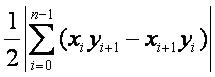
如果逆时针给出点坐标,值为正,
如果顺时针给出点坐标,值为负。
Bash游戏:
有一堆石子共有N个。A B两个人轮流拿,A先拿。每次最少拿1颗,最多拿K颗,拿到最后1颗石子的人获胜。
若n不足k+1,则A第一次取完,A胜。
若n是k+1的倍数,每次A取x,B都能取k+1-x,B胜。
否则,A胜。
威佐夫游戏:
有2堆石子。A B两个人轮流拿,A先拿。每次可以从一堆中取任意个或从2堆中取相同数量的石子,但不可不取。
两堆石头x < y,若(y-x)*(sqrt(5)+1) / 2+1) == x,则B胜。否则A胜。
1/a循环节长度:
a先约去2和5的因子->b,然后球欧拉函数值ϕ,求一个最小的x,使得x|ϕ且10^x%b == 1。

#include<bits/stdc++.h> #define eps 1e-8 #define PI acos(-1) using namespace std; int sgn(double x) { if(fabs(x) < eps) return 0; if(x < 0) return -1; return 1; } struct point { double x,y; point(){}; point(double a,double b):x(a),y(b){}; friend point operator+(point a,point b) //向量加法 { return point(a.x+b.x,a.y+b.y); } friend point operator-(point a,point b) //向量减法 { return point(a.x-b.x,a.y-b.y); } friend double operator*(point a,point b) //点积 { return a.x*b.x+a.y*b.y; } friend double operator^(point a,point b) //叉积 { return a.x*b.y-a.y*b.x; } void trans(double B) //绕原点旋转弧度B { double tx = x,ty = y; x = tx*cos(B)-ty*sin(B); y = tx*sin(B)+ty*cos(B); } }; struct line { point s,e; line(){}; line(point a,point b):s(a),e(b){}; friend pair<int,point> operator&(line a,line b) //重合0,平行1,相交2 { point ans = a.s; if(sgn((a.s-a.e)^(b.s-b.e)) == 0) { if(sgn((a.s-b.e)^(b.s-b.e)) == 0) return make_pair(0,ans); //重合 return make_pair(1,ans); //平行 } double t = ((a.s-b.s)^(b.s-b.e))/((a.s-a.e)^(b.s-b.e)); ans.x += (a.e.x-a.s.x)*t; ans.y += (a.e.y-a.s.y)*t; return make_pair(2,ans); } }; double dis(point a,point b) //两点距离 { return sqrt((a-b)*(a-b)); } point dis2(point p,line l) //点到直线距离,返回垂点 { point ans; double t = ((p-l.s)*(l.e-l.s))/((l.e-l.s)*(l.e-l.s)); ans.x = l.s.x+(l.e.x-l.s.x)*t; ans.y = l.s.y+(l.e.y-l.s.y)*t; return ans; } point dis3(point p,line l) //点到线段距离,返回线段上最近的点 { point ans; double t = ((p-l.s)*(l.e-l.s))/((l.e-l.s)*(l.e-l.s)); if(t >= 0 && t <= 1) { ans.x = l.s.x+(l.e.x-l.s.x)*t; ans.y = l.s.y+(l.e.y-l.s.y)*t; } else if(dis(p,l.s) < dis(p,l.e)) ans = l.s; else ans = l.e; return ans; } bool inter(line a,line b) //判断线段相交 { double x1 = a.s.x,y1 = a.s.y,x2 = a.e.x,y2 = a.e.y,x3 = b.s.x,y3 = b.s.y,x4 = b.e.x,y4 = b.e.y; double t1 = (x2-x1)*(y3-y2)-(x3-x2)*(y2-y1); double t2 = (x2-x1)*(y4-y2)-(x4-x2)*(y2-y1); double t3 = (x4-x3)*(y1-y4)-(x1-x4)*(y4-y3); double t4 = (x4-x3)*(y2-y4)-(x2-x4)*(y4-y3); return t1*t2 <= 0 && t3*t4 <= 0; } bool inter2(line a,line b) //判断直线a和线段b相交 { return sgn((b.s-a.e)^(a.s-a.e))*sgn((b.e-a.e)^(a.s-a.e)) <= 0; } bool online(point p,line l) //判断点在直线上 { return sgn((l.s-p)^(l.e-p)) == 0; } bool onseg(point p,line l) //判断点在线段上 { return sgn((l.s-p)^(l.e-p)) == 0 && sgn((p.x-l.s.x)*(p.x-l.e.x)) <= 0 && sgn((p.y-l.s.y)*(p.y-l.e.y)) <= 0; } bool onconvex(point a,point *p,int n) //判断点在凸多边形(凸包,点逆时针,若顺时针改为>0)内,-1在外,0在边上,1在内 { for(int i = 1;i <= n;i++) { int j = i+1; if(j > n) j = 1; if(sgn((p[i]-a)^(p[j]-a)) < 0) return -1; if(onseg(a,line(p[i],p[j]))) return 0; } return 1; } bool onpoly(point a,point *p,int n) //判断点在多边形内,-1在外,0在边上,1在内 { int cnt = 0; line ray = line(a,point(-1e9,a.y)); for(int i = 1;i <= n;i++) { int j = i+1; if(j > n) j = 1; line side = line(p[i],p[j]); if(onseg(a,side)) return 0; if(sgn(side.s.y-side.e.y) == 0) continue; if(onseg(side.s,ray)) { if(sgn(side.s.y-side.e.y) > 0) cnt++; } else if(onseg(side.e,ray)) { if(sgn(side.e.y-side.s.y) > 0) cnt++; } else if(inter(ray,side)) cnt++; } if(cnt%2) return 1; return -1; } double calcarea(point *p,int n) //计算多边形面积,可顺时针或逆时针 { double ans = 0; for(int i = 1;i <= n;i++) { int j = i+1; if(j > n) j = 1; ans += (p[i]^p[j])/2; } return fabs(ans); } bool isconvex(point *p,int n) //判断是否凸多边形,允许共线边,可顺时针或逆时针 { bool s[3] = {0}; for(int i = 1;i <= n;i++) { int j = i+1,k = j+2; if(j > n) j -= n; if(k > n) k -= n; s[sgn((p[j]-p[i])^(p[k]-p[i]))+1] = 1; if(s[0] && s[2]) return 0; } return 1; } int main() { point a = dis2(point(2,2),line(point(0,2),point(2,0))); cout <<a.x << " " << a.y << endl; return 0; }

bool isface(int x1,int y1,int z1,int x2,int y2,int z2,int x3,int y3,int z3,int x4,int y4,int z4) { int a11 = x1-x2,a12 = x2-x3,a13 = x3-x4; int a21 = y1-y2,a22 = y2-y3,a23 = y3-y4; int a31 = z1-z2,a32 = z2-z3,a33 = z3-z4; return a11*a22*a33+a12*a23*a31+a13*a21*a32-a13*a22*a31-a11*a23*a32-a12*a21*a33 == 0; }

bool trianglecircle(int XX,int YY,int R,int X1,int Y1,int X2,int Y2,int X3,int Y3) { double a1 = (X1-XX)*(X1-XX)+(Y1-YY)*(Y1-YY); double a2 = (X2-XX)*(X2-XX)+(Y2-YY)*(Y2-YY); double a3 = (X3-XX)*(X3-XX)+(Y3-YY)*(Y3-YY); double rr = R*R; if(a1 < rr-1e-6 && a2 < rr-1e-6 && a3 < rr-1e-6) return 1; if(a1 > rr+1e-6 && a2 > rr+1e-6 && a3 > rr+1e-6) { double t = ((XX-X1)*(X2-X1)+(YY-Y1)*(Y2-Y1))*((XX-X2)*(X1-X2)+(YY-Y2)*(Y1-Y2)); if(t > 1e-6) { t = abs((X1-XX)*(Y2-YY)-(X2-XX)*(Y1-YY))/sqrt((X1-X2)*(X1-X2)+(Y1-Y2)*(Y1-Y2)); if(t*t < rr+1e-6) return 0; } t = ((XX-X3)*(X2-X3)+(YY-Y3)*(Y2-Y3))*((XX-X2)*(X3-X2)+(YY-Y2)*(Y3-Y2)); if(t > 1e-6) { t = abs((X3-XX)*(Y2-YY)-(X2-XX)*(Y3-YY))/sqrt((X3-X2)*(X3-X2)+(Y3-Y2)*(Y3-Y2)); if(t*t < rr+1e-6) return 0; } t = ((XX-X3)*(X1-X3)+(YY-Y3)*(Y1-Y3))*((XX-X1)*(X3-X1)+(YY-Y1)*(Y3-Y1)); if(t > 1e-6) { t = abs((X3-XX)*(Y1-YY)-(X1-XX)*(Y3-YY))/sqrt((X3-X1)*(X3-X1)+(Y3-Y1)*(Y3-Y1)); if(t*t < rr+1e-6) return 0; } return 1; } return 0; }

struct node { int x,y; friend bool operator <(node a,node b) { if(a.x == b.x) return a.y<b.y; return a.x<b.x; } }a[1005],ans[1005]; int n,m; int cross(node a,node b,node c)//向量积 { return (a.x-c.x)*(b.y-c.y)-(b.x-c.x)*(a.y-c.y); } int convex(int n)//求凸包上的点 { sort(a+1,a+n+1); int m = 0; for(int i = 1;i <= n;i++) { while(m > 1 && cross(ans[m],a[i],ans[m-1])<=0) m--; ans[++m] = a[i]; } int k = m; //求得上凸包 for(int i = n-1;i >= 1;i--) { while(m > k && cross(ans[m],a[i],ans[m-1])<=0) m--; ans[++m] = a[i]; } if(n > 2) m--;//起始点重复。 return m; }

point waixin(point a,point b,point c) //求三角形外心 { double a1 = b.x-a.x,b1 = b.y-a.y,c1 = (a1*a1+b1*b1)/2; double a2 = c.x-a.x,b2 = c.y-a.y,c2 = (a2*a2+b2*b2)/2; double d = a1*b2-a2*b1; return point(a.x+(c1*b2-c2*b1)/d,a.y+(a1*c2-a2*c1)/d); }

double circlrarea(point a1,int r1,point a2,int r2) //计算两圆相交面积 { double d = dis(a1,a2); if(r1+r2 < d+eps) return 0; if(d < fabs(r1-r2)+eps) { double r = min(r1,r2); return PI*r*r; } double x = (d*d+r1*r1-r2*r2)/(2*d); double t1 = acos(x/r1),t2 = acos((d-x)/r2); return r1*r1*t1+r2*r2*t2-d*r1*sin(t1); }

#include<bits/stdc++.h> using namespace std; int n,b[100005]; struct xx { double x,y; friend bool operator<(xx a,xx b) { return a.x < b.x; } }a[100005]; bool cmp(int x,int y) { return a[x].y < a[y].y; } double dis(xx a,xx b) { return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)); } double f(int l,int r) { if(l == r) return 0; if(r-l == 1) return dis(a[l],a[r]); if(r-l == 2) { double minn = 1e18; minn = min(minn,dis(a[l],a[l+1])); minn = min(minn,dis(a[l],a[r])); minn = min(minn,dis(a[l+1],a[r])); return minn; } int mid = (l+r)/2; double minn = min(f(l,mid),f(mid+1,r)); int cnt = 0; for(int i = l;i <= r;i++) { if(a[i].x >= a[mid].x-minn && a[i].x <= a[mid].x+minn) b[++cnt] = i; } sort(b+1,b+1+cnt,cmp); for(int i = 1;i <= cnt;i++) { for(int j = i+1;j <= cnt;j++) { if(a[b[j]].y-a[b[i]].y > minn) break; minn = min(minn,dis(a[b[i]],a[b[j]])); } } return minn; } int main() { while(scanf("%d",&n) && n) { for(int i = 1;i <= n;i++) scanf("%lf%lf",&a[i].x,&a[i].y); sort(a+1,a+1+n); printf("%.2f\n",f(1,n)/2); } return 0; }

#include<bits/stdc++.h> #define eps 1e-8 #define PI acos(-1) using namespace std; int sgn(double x) { if(fabs(x) < eps) return 0; if(x < 0) return -1; return 1; } struct point { double x,y; point(){}; point(double a,double b):x(a),y(b){}; friend point operator+(point a,point b) //向量加法 { return point(a.x+b.x,a.y+b.y); } friend point operator-(point a,point b) //向量减法 { return point(a.x-b.x,a.y-b.y); } friend double operator*(point a,point b) //点积 { return a.x*b.x+a.y*b.y; } friend double operator^(point a,point b) //叉积 { return a.x*b.y-a.y*b.x; } }ans[20005]; struct line { point s,e; double k; line(){}; line(point a,point b):s(a),e(b) { k = atan2(e.y-s.y,e.x-s.x); }; friend point operator&(line a,line b) { point ans = a.s; double t = ((a.s-b.s)^(b.s-b.e))/((a.s-a.e)^(b.s-b.e)); ans.x += (a.e.x-a.s.x)*t; ans.y += (a.e.y-a.s.y)*t; return ans; } }a[20005],q[20005]; bool HPIcmp(line a,line b) //直线左边 { if(fabs(a.k - b.k) > eps) return a.k < b.k; return ((a.s - b.s)^(b.e - b.s)) < 0; } //返回核的凸包点 void HPI(line *a,int n,point *ans,int &cnt) { sort(a+1,a+n+1,HPIcmp); int tot = 0; for(int i = 1;i <= n;i++) { if(fabs(a[i].k-a[i-1].k) > eps) a[++tot] = a[i]; } int head = 0,tail = 1; q[0] = a[1]; q[1] = a[2]; cnt = 0; for(int i = 3;i <= tot;i++) { if(fabs((q[tail].e-q[tail].s)^(q[tail-1].e-q[tail-1].s)) < eps || fabs((q[head].e-q[head].s)^(q[head+1].e-q[head+1].s)) < eps) return; while(head < tail && (((q[tail]&q[tail-1])-a[i].s)^(a[i].e-a[i].s)) > eps) tail--; while(head < tail && (((q[head]&q[head+1])-a[i].s)^(a[i].e-a[i].s)) > eps) head++; q[++tail] = a[i]; } while(head < tail && (((q[tail]&q[tail-1])-q[head].s)^(q[head].e-q[head].s)) > eps) tail--; while(head < tail && (((q[head]&q[head-1])-q[tail].s)^(q[tail].e-q[tail].e)) > eps) head++; if(tail <= head+1) return; for(int i = head;i < tail;i++) ans[++cnt] = q[i]&q[i+1]; if(head < tail-1) ans[++cnt] = q[head]&q[tail]; }

struct point { int x,y; point(){}; point(int a,int b):x(a),y(b){}; friend point operator-(point a,point b) //向量减法 { return point(a.x-b.x,a.y-b.y); } friend double operator^(point a,point b) //叉积 { return a.x*b.y-a.y*b.x; } friend double operator*(point a,point b) //点积 { return a.x*b.x+a.y*b.y; } friend bool operator <(point a,point b) { if(a.x == b.x) return a.y < b.y; return a.x < b.x; } }a[50005],ans[50005]; int n,m; int cross(point a,point b,point c)//向量积 { return (a.x-c.x)*(b.y-c.y)-(b.x-c.x)*(a.y-c.y); } int dis2(point a,point b) { return (a-b)*(a-b); } int convex(int n)//求凸包上的点 { sort(a+1,a+n+1); int m = 0; for(int i = 1;i <= n;i++) { while(m > 1 && cross(ans[m],a[i],ans[m-1])<=0) m--; ans[++m] = a[i]; } int k = m; //求得上凸包 for(int i = n-1;i >= 1;i--) { while(m > k && cross(ans[m],a[i],ans[m-1])<=0) m--; ans[++m] = a[i]; } if(n > 2) m--;//起始点重复。 return m; } int rotatingcalipers(point *a,int n) { int ans = 0,now = 2,ne = 3; if(ne > n) ne = 1; for(int i = 1;i <= n;i++) { int j = i+1; if(j > n) j = 1; point t = a[i]-a[j]; while((t^(a[ne]-a[now])) < 0) { now = ne; ne = now+1; if(ne > n) ne = 1; } ans = max(ans,max(dis2(a[i],a[now]),dis2(a[j],a[ne]))); } return ans; } int main() { while(~scanf("%d",&n)) { for(int i = 1;i <= n;i++) scanf("%d%d",&a[i].x,&a[i].y); m = convex(n); printf("%d\n",rotatingcalipers(ans,m)); } }

//已求得凸包 int rotatingcalipers(point *a,int n) { int ans = 0; for(int i = 1;i <= n;i++) { int j = i+1; if(j > n) j = 1; int k = j+1; if(k > n) k = 1; int kk = k+1; if(kk > n) kk = 1; while(j != i && k != i) { ans = max(ans,abs((a[j]-a[i]^(a[k]-a[i])))); while(((a[i]-a[j])^(a[kk]-a[k])) < 0) { k = kk; kk++; if(kk > n) kk = 1; } } } return ans; }

double dis4(point a,point b,point c) { return dis(a,dis3(a,line(b,c))); } double dis5(point a,point b,point c,point d) { double ans1 = min(dis4(a,c,d),dis4(b,c,d)); double ans2 = min(dis4(c,a,b),dis4(d,a,b)); return min(ans1,ans2); } double getangel(point a,point b,point c,point d) { return (b-a)^(d-c); } int rotatingcalipers(point *a,int n,point *b,int m) { int sa = 1,sb = 1; for(int i = 1;i <= n;i++) { if(sgn(a[i].y-a[sa].y) < 0) sa = i; } for(int i = 1;i <= m;i++) { if(sgn(b[i].y-b[sb].y) < 0) sb = i; } double t,ans = dis(a[sa],b[sb]); int na = sa+1,nb = sb+1; if(na > n) na = 1; if(nb > m) nb = 1; for(int i = 1;i <= n;i++) { while(sgn(t = getangel(a[sa],a[na],b[sb],b[nb])) < 0) { sb = nb; nb++; if(nb > m) nb = 1; } if(sgn(t) == 0) ans = min(ans,dis5(a[sa],a[na],b[sb],b[nb])); else ans = min(ans,dis4(b[sb],a[sa],a[na])); sa = na; na++; if(na > n) na = 1; } return ans; } //已求得凸包 double solve(point *a,int n,point *b,int m) { return min(rotatingcalipers(a,n,b,m),rotatingcalipers(b,m,a,n)); }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号