算法练习——完全数

  完全数
  定义：数的因子就是所有可以整除这个数的数,但是不包括这个数自身。比如15的因子是1, 3, 5 。
如果一个正整数如果正好等于它的所有因子之和，这个数就称为“完数”。例如，6的因子为
1, 2, 3, 而6＝1＋2＋3，因此6是“完数”。
维基百科：
    完全数： https://zh.wikipedia.org/zh-cn/%E5%AE%8C%E5%85%A8%E6%95%B0
    梅森素数：https://zh.wikipedia.org/zh-cn/%E6%A2%85%E6%A3%AE%E7%B4%A0%E6%95%B0

    古希腊数学家欧几里得是通过 的表达式发现前四个完全数的。

当

当

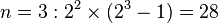
当

当

  一个偶数是完美数，当且仅当它具有如下形式：，其中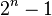是素数，此事实的充分性由欧几里得证明，而必要性则由欧拉所证明。

　　梅森数是指形如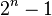的数，记为；如果一个梅森数是素数那么它称为梅森素数。

      当n为合数时，一定为合数。

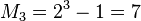      当n为素数时，不一定皆为素数，比如和是素数，但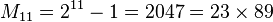却不是素数。

算法：

#include"stdafx.h"
#include<stdio.h>
#include<math.h>

/**
  完全数
  数的因子就是所有可以整除这个数的数,但是不包括这个数自身。比如15的因子是1, 3, 5 。
如果一个正整数如果正好等于它的所有因子之和，这个数就称为“完数”。例如，6的因子为
1, 2, 3, 而6＝1＋2＋3，因此6是“完数”。
维基百科：
    完全数： https://zh.wikipedia.org/zh-cn/%E5%AE%8C%E5%85%A8%E6%95%B0
    梅森素数：https://zh.wikipedia.org/zh-cn/%E6%A2%85%E6%A3%AE%E7%B4%A0%E6%95%B0
*/
int func(int n);
void func2();
int main()
{
     printf("方案一：因式分解求和\n");
     int n;
     for(int i = 2; i <1000; i=i+2){ //1000以下都是偶数
         if(func(i)){
            printf("%d\t",i);
         }        
     }
     printf("\n方案二：使用数学公式\n");
     func2();
     getchar();
     return 0;
}

// 方案一： 直接因子求和
int func(int n){
    int d = 1,a;
    a = int(sqrt(1.0*n));  //对一个数,最多判断n开平方次
    for(int i = 2; i <= a; i++){
       if (n%i == 0)   //说明n能被b整除
        d += i + n/i;
    }  
    return  d==n;
}
//方案二： 数学公式 2^{n-1}*(2^n-1),n为素数
void func2(){
    int n,p[4]={2,3,5,7};
    for(int i=0;i<4;i++){
        n= pow(2.0,p[i]-1)*(pow(2.0,p[i])-1);
        if(n<1000)
            printf("%d\t",n);
        else        
            break;
    }
}