用队列和栈的知识点解决迷宫问题
迷宫问题
这里有一个迷宫如图所示,求走出迷宫的路径
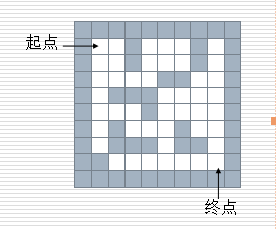
这里我们建一个二维列表,表示迷宫(0表示通道,1表示围墙)。
maze = [ [1,1,1,1,1,1,1,1,1,1], [1,0,0,1,0,0,0,1,0,1], [1,0,0,1,0,0,0,1,0,1], [1,0,0,0,0,1,1,0,0,1], [1,0,1,1,1,0,0,0,0,1], [1,0,0,0,1,0,0,0,0,1], [1,0,1,0,0,0,1,0,0,1], [1,0,1,1,1,0,1,1,0,1], [1,1,0,0,0,0,0,0,0,1], [1,1,1,1,1,1,1,1,1,1] ]
用栈解决迷宫问题
基本思路:在一个迷宫节点(x,y)上,可以进行四个方向的探查:maze[x-1][y](表示上), maze[x+1][y](下), maze[x][y-1](左), maze[x][y+1](右)
思路:从一个节点开始,任意找下一个能走的点,当找不到能走的点时,退回上一个点寻找是否有其他方向的点。
方法:创建一个空栈,首先将入口位置进栈。当栈不空时循环:获取栈顶元素,寻找下一个可走的相邻方块,如果找不到可走的相邻方块,说明当前位置是死胡同,进行回溯(就是讲当前位置出栈,看前面的点是否还有别的出路)
maze = [ [1,1,1,1,1,1,1,1,1,1], [1,0,0,1,0,0,0,1,0,1], [1,0,0,1,0,0,0,1,0,1], [1,0,0,0,0,1,1,0,0,1], [1,0,1,1,1,0,0,0,0,1], [1,0,0,0,1,0,0,0,0,1], [1,0,1,0,0,0,1,0,0,1], [1,0,1,1,1,0,1,1,0,1], [1,1,0,0,0,0,0,0,0,1], [1,1,1,1,1,1,1,1,1,1] ] dirs = [ lambda x,y:(x-1,y), #上 lambda x,y:(x,y+1), #右 lambda x,y:(x+1,y), #下 lambda x,y:(x,y-1), #左 ] def stack_solve_maze(x1, y1, x2, y2): """ :param x1: 起点x坐标 :param y1: 起点y坐标 :param x2: 终点x坐标 :param y2: 终点y坐标 :return: """ stack = [] stack.append((x1,y1))#起点 maze[x1][y1] = 2#2表示已经走过的点,我们要将已经走过的点进行标识,免得走重复的路 while len(stack) > 0: # 当栈不空循环 cur_node = stack[-1]#栈顶,即目前所在位置 if cur_node == (x2,y2): #到达终点 for p in stack: print('==>',p,end='')#依次输出栈内坐标 return True #没到终点时,在任意位置都要试探上下左右是否走得通 for dir in dirs: next_node = dir(*cur_node) if maze[next_node[0]][next_node[1]] == 0: #0是通道,说明找到一个能走的方向 stack.append(next_node) maze[next_node[0]][next_node[1]] = 2 # 2表示已经走过的点 break else: #如果一个方向也找不到,说明到死胡同了 stack.pop() else: print("无路可走") return False stack_solve_maze(1,1,8,8) #==> (1, 1)==> (1, 2)==> (2, 2)==> (3, 2)==> (3, 1)==> (4, 1)==> (5, 1)==> (5, 2)==> (5, 3)==> (6, 3)==> (6, 4)==>
#(6, 5)==> (5, 5)==> (4, 5)==> (4, 6)==> (4, 7)==> (3, 7)==> (3, 8)==> (4, 8)==> (5, 8)==> (6, 8)==> (7, 8)==> (8, 8)
用队列解决迷宫问题
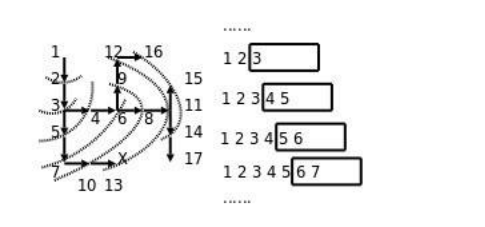
思路:从一个节点开始,寻找所有下面能继续走的点。继续寻找,直到找到出口。
方法:创建一个空队列,将起点位置进队。在队列不为空时循环:出队一次。如果当前位置为出口,则结束算法;否则找出当前方块的4个相邻方块中可走的方块,全部进队。
from collections import deque maze = [ [1,1,1,1,1,1,1,1,1,1], [1,0,0,1,0,0,0,1,0,1], [1,0,0,1,0,0,0,1,0,1], [1,0,0,0,0,1,1,0,0,1], [1,0,1,1,1,0,0,0,0,1], [1,0,0,0,1,0,0,0,0,1], [1,0,1,0,0,0,1,0,0,1], [1,0,1,1,1,0,1,1,0,1], [1,1,0,0,0,0,0,0,0,1], [1,1,1,1,1,1,1,1,1,1] ] dirs = [ lambda x,y:(x-1,y), #上 lambda x,y:(x,y+1), #右 lambda x,y:(x+1,y), #下 lambda x,y:(x,y-1), #左 ] def deque_solve_maze(x1,y1,x2,y2): queue = deque()#创建队列 path = [] # 记录出队之后的节点 queue.append((x1,y1,-1)) maze[x1][y1] = 2#2表示应经走过的点 while len(queue) > 0: cur_node = queue.popleft() path.append(cur_node) if cur_node[0] == x2 and cur_node[1] == y2: #到终点 real_path = [] x,y,i = path[-1] real_path.append((x,y))#将终点坐标append到real_path中 while i >= 0: node = path[i]#node是一个元祖(x坐标,y坐标,该点的leader) real_path.append(node[0:2])#只要坐标 i = node[2] real_path.reverse()#反转后顺序才为从起点到终点 for p in real_path: print('==>',p,end='') return True for dir in dirs: next_node = dir(cur_node[0], cur_node[1]) if maze[next_node[0]][next_node[1]] == 0: queue.append((next_node[0], next_node[1], len(path)-1)) maze[next_node[0]][next_node[1]] = 2 # 标记为已经走过 else: print("无路可走") return False deque_solve_maze(1,1,8,8) #==> (1, 1)==> (2, 1)==> (3, 1)==> (4, 1)==> (5, 1)==> (5, 2)==> (5, 3)==> (6, 3)==> (6, 4)==> #(6, 5)==> (7, 5)==> (8, 5)==> (8, 6)==> (8, 7)==> (8, 8)
总结
栈解决迷宫问题占用内存相对较小,但用栈找到的出路只是所有出路中的其中一条,具体是哪一条取决于dir列表中上下左右位置定义的顺序。
队列解决迷宫问题找到的出路肯定是最短路径,但是相对而言用队列会比较占用内存。


