what's the 二叉树
what's the 树
在了解二叉树之前,首先我们得有树的概念。
树是一种数据结构又可称为树状图,如文档的目录、HTML的文档树都是树结构,它是由n(n>=1)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
-
- 每个节点有零个或多个子节点;
-
- 没有父节点的节点称为根节点;
-
- 每一个非根节点有且只有一个父节点;
-
- 除了根节点外,每个子节点可以分为多个不相交的子树;
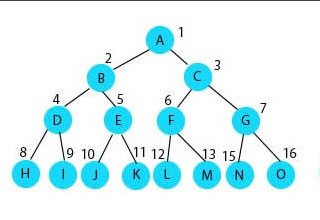
有关树的一些相关术语:
-
- 节点的度:一个节点含有的子树的个数称为该节点的度;
-
- 叶节点或终端节点:度为0的节点称为叶节点;
-
- 非终端节点或分支节点:度不为0的节点;
-
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
-
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
-
- 兄弟节点:具有相同父节点的节点互称为兄弟节点;
-
- 树的度:一棵树中,最大的节点的度称为树的度;
-
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
-
- 树的高度或深度:树中节点的最大层次;
-
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟;
-
- 节点的祖先:从根到该节点所经分支上的所有节点;
-
- 森林:由m(m>=0)棵互不相交的树的集合称为森林;
树的种类有:无序树、有序树、二叉树、霍夫曼树。其中最重要应用最多的就是二叉树,下面我们来学习有关二叉树的知识。
二叉树
二叉树的定义为度不超过2的树,即每个节点最多有两个叉(两个分支)。上面那个例图其实就是一颗二叉树。
二叉树有两个特殊的形态:满二叉树和完全二叉树
满二叉树
一个二叉树,如果除了叶子节点外每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。
完全二叉树
叶节点只能出现在最下层和次下层,并且最下面一层的结点都集中在该层最左边的若干位置的二叉树为完全二叉树。即右边的最下层和次下层可以适当缺一个右子数
完全二叉树是效率很高的数据结构

二叉树的遍历
二叉树的链式存储:将二叉树的节点定义为一个对象,节点之间通过类似链表的链接方式来连接。
二叉树结点的定义
#二叉树结点的定义 class BiTreeNode: def __init__(self, data): self.data = data self.lchild = None self.rchild = None
二叉树的遍历分为四种——前序遍历、中序遍历、后序遍历和层级遍历
设树结构为:
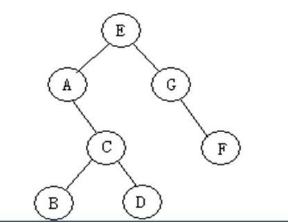
- 前序遍历:先打印根,再递归其左子树,后递归其右子数 E ACBD GF
- 中序遍历:以根为中心,左边打印左子树,右边打印右子树(注意,每个子树也有相应的根和子树) A BCD E GF
- 后序遍历:先递归左子树,再递归右子树,后打印根(注意,每个子树也有相应的根和子树BDC A FG E
- 层次遍历:从根开始一层一层来,同一层的从左到右输出E AG CF BD
四种遍历方法的代码实现:

from collections import deque #结点的定义 class BiTreeNode: def __init__(self, data): self.data = data self.lchild = None self.rchild = None #二叉树结点 a = BiTreeNode('A') b = BiTreeNode('B') c = BiTreeNode('C') d = BiTreeNode('D') e = BiTreeNode('E') f = BiTreeNode('F') g = BiTreeNode('G') #结点之间的关系 e.lchild = a e.rchild = g a.rchild = c c.lchild = b c.rchild = d g.rchild = f root = e #前序遍历:先打印根,再递归左孩子,后递归右孩子 def pre_order(root): if root: print(root.data, end='') pre_order(root.lchild) pre_order(root.rchild) #中序遍历:以根为中心,左边打印左子树,右边打印右子树(注意,每个子树也有相应的根和子树) #(ACBD) E (GF)-->(A(CBD)) E (GF)-->(A (B C D)) E (G F) def in_order(root): if root: in_order(root.lchild) print(root.data, end='') in_order(root.rchild) #后序遍历:先递归左子树,再递归右子数,后打印根(注意,每个子树也有相应的根和子树) # (ABCD)(GF)E-->((BCD)A)(GF)E-->(BDCA)(FG)E def post_order(root): if root: post_order(root.lchild) post_order(root.rchild) print(root.data, end='') #层次遍历:一层一层来,同一层的从左到右输出 def level_order(root): queue = deque() queue.append(root) while len(queue) > 0: node = queue.popleft() print(node.data,end='') if node.lchild: queue.append(node.lchild) if node.rchild: queue.append(node.rchild) pre_order(root)#EACBDGF print("") in_order(root)#ABCDEGF print("") post_order(root)#BDCAFGE print("") level_order(root)#EAGCFBD
二叉搜索树
二叉搜索树(Binary Search Tree),它或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉搜索树。
二叉搜索树一个很好玩的网址,集成了增删改的功能:https://visualgo.net/en/bst
二叉搜索树的中序遍历得到的是原来列表按升序排序的列表
由列表生成二叉搜索树、通过二叉搜索树查询值和删除值的示例代码:

#结点定义 class BiTreeNode: def __init__(self, data): self.data = data self.lchild = None self.rchild = None #建立二叉搜索树(循环列表,插入值) class BST: def __init__(self, li=None): self.root = None if li: self.root = self.insert(self.root, li[0])#列表的第一个元素是根 for val in li[1:]: self.insert(self.root, val) #生成二叉搜索树递归版本 def insert(self, root, val): if root is None: root = BiTreeNode(val) elif val < root.data:#插入的值小于root,要放到左子树中(递归查询插入的位置) root.lchild = self.insert(root.lchild, val) else:#插入的值大于root,要放到右子树中(递归查询插入的位置) root.rchild = self.insert(root.rchild, val) return root #生成二叉搜索树不递归的版本 def insert_no_rec(self, val): p = self.root if not p: self.root = BiTreeNode(val) return while True: if val < p.data: if p.lchild: p = p.lchild else: p.lchild = BiTreeNode(val) break else: if p.rchild: p = p.rchild else: p.rchild = BiTreeNode(val) break #查询递归版本 def query(self, root, val): if not root: return False if root.data == val: return True elif root.data > val: return self.query(root.lchild, val) else: return self.query(root.rchild, val) #查询非递归版本 def query_no_rec(self, val): p = self.root while p: if p.data == val: return True elif p.data > val: p = p.lchild else: p = p.rchild return False #中序遍历,得到的是升序的列表 def in_order(self, root): if root: self.in_order(root.lchild) print(root.data, end=',') self.in_order(root.rchild) tree = BST() for i in [1,5,9,8,7,6,4,3,2]: tree.insert_no_rec(i) tree.in_order(tree.root) #print(tree.query_no_rec(12))
二叉搜索树的应用——AVL树、B树、B+树
AVL树
AVL树:AVL树是一棵自平衡的二叉搜索树。
AVL树具有以下性质: 根的左右子树的高度之差的绝对值不能超过1 根的左右子树都是平衡二叉树
AVL的实现方式:旋转

B树
B树是一棵自平衡的多路搜索树。常用于数据库的索引。
在B-树中查找给定关键字的方法是,首先把根结点取来,在根结点所包含的关键字K1,…,Kn查找给定的关键字(可用顺序查找或二分查找法),若找到等于给定值的关键字,则查找成功;否则,一定可以确定要查找的关键字在Ki与Ki+1之间,Pi为指向子树根节点的指针,此时取指针Pi所指的结点继续查找,直至找到,或指针Pi为空时查找失败。
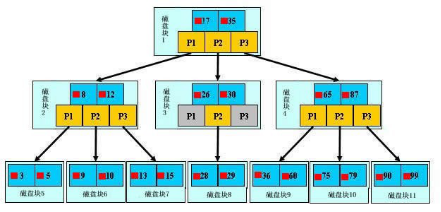
B+ 树
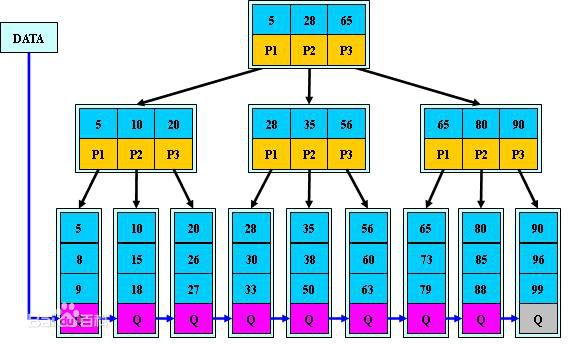
B+树的查找
|
1
2
3
4
5
6
7
8
9
10
|
Function: search (k) return tree_search (k, root); Function: tree_search (k, node) if node is a leaf then return node; switch k do case k < k_0 return tree_search(k, p_0); case k_i ≤ k < k_{i+1} return tree_search(k, p_{i+1}); case k_d ≤ k return tree_search(k, p_{d+1});//伪代码假设没有重复值 |
B+树的插入
B+树的删除



