最短路+最短路条数+记录全部路径java实现
核心代码:

package com.ltsj.web.algorithm.operator; import com.ltsj.web.meta.common.utils.ArithUtil; import com.sun.javafx.geom.Edge; import java.util.*; /** * @Author zl * @Description 网络节点介数中心性计算 * @Date 2022/1/6 11:26 */ public class Betweeness { /** * MAX_VALUE表示无穷大,代表两个网络节点距离不能到达 * Double.MAX_VALUE,Double.MAX_VALUE相加会溢出导致出现负权 */ public static final double MAX_VALUE = Double.MAX_VALUE / 3; /** * 网络图节点个数 */ private static int n; /** * 网络边的邻接表 */ private static Edge[] edge; /** * 网络边的邻接表(反向邻接表,用于最短路径记录回溯) */ private static Edge[] edge2; /** * 起点和终点 */ static int s, t; /** * 头 */ static int[] head; /** * */ static int num; /** * num2 */ static int num2; /** * head2 */ static int[] head2; /** * 最短路径长度 */ static double[] dis; /** * 标记节点是否走过 */ static boolean[] vis; /** * 记录最短路径(多条) */ static List<List<Integer>> se; /** * 数据初始化 * @author: zl * @date: 2022/1/6 17:40 */ static void init(double[][] matrix) { n = matrix.length; head = new int[n * n]; head2 = new int[n * n]; dis = new double[n]; vis = new boolean[n]; se = new ArrayList<>(); edge = new Edge[n * n]; edge2 = new Edge[n * n]; for (int i = 0; i < n; i++) { head[i] = -1; head2[i] = -1; } num = 0; num2 = 0; } /** * 求最短路 * @param st: 起点 * @return: void * @author: zl * @date: 2022/1/6 17:41 */ public static void dijstra(int st) { for (int i = 0; i < n; i++) { dis[i] = MAX_VALUE; vis[i] = false; } dis[st] = 0; Queue<Node> que = new PriorityQueue<>(); que.add(new Node(st, 0)); while (!que.isEmpty()) { Node p = que.element(); que.poll(); int nown = p.num; if (vis[nown]) { continue; } vis[nown] = true; for (int i = head[nown]; i != -1; i = edge[i].next) { Edge e = edge[i]; if (dis[e.v] > dis[nown] + e.w && !vis[e.v]) { dis[e.v] = dis[nown] + e.w; que.add(new Node(e.v, dis[e.v])); } } } } /** * 通过终点递归回溯查找所有最短路径 * @param t: 终点 * @param vec:路径记录集合 * @author: zl * @date: 2022/1/6 17:41 */ static void prinPath(int t, List<Integer> vec) { vec.add(t); if (t == s) { //Collections.reverse(vec); se.add(new ArrayList<>(vec)); /*vec = new ArrayList<>(); vec.add(DijstraAlgorithm3.t);*/ vec.remove(new Integer(t)); return; } for (int i = head2[t]; i != -1; i = edge2[i].next) { int v = edge2[i].v; double w = edge2[i].w; if (dis[v] == dis[t] - w) { //System.out.println(v+"----"+t); prinPath(v, vec); vec.remove(new Integer(v)); /*vec = new ArrayList<>(); vec.add(t);*/ } } } static void addEdge(int u, int v, double w) { Edge newEdge = new Edge(u, v, head[u], w); edge[num] = newEdge; head[u] = num++; } static void addEdge2(int u, int v, double w) { Edge newEdge = new Edge(u, v, head2[u], w); edge2[num2] = newEdge; head2[u] = num2++; } /** 节点对象 * @author: zl * @date: 2022/1/7 14:47 */ static class Node implements Comparable<Node> { int num;//存编号 double val; //和距离 public Node() { this.num = 0; this.val = 0; } public Node(int num, double val) { this.num = num; this.val = val; } @Override public int compareTo(Node o) { if (val > o.val) { return 1; } else if (val < o.val) { return -1; } else { return 0; } } } /** * 边对象 * @author: zl * @date: 2022/1/7 14:47 */ static class Edge { int u, v, next; double w; public Edge() { } public Edge(int u, int v, int next, double w) { this.u = u; this.v = v; this.next = next; this.w = w; } @Override public String toString() { return "Edge{" + "u=" + u + ", v=" + v + ", next=" + next + ", w=" + w + '}'; } } /** * 计算网络图节点介数中心性 * @param matrix: 网络图矩阵 * @return: 计算结果(节点介数中心性) * @author: zl * @date: 2022/1/7 14:38 */ public static double[] calculateBetweeness(double[][] matrix){ init(matrix); for (int i = 0; i < matrix.length; i++) { for (int j = 0; j < matrix.length; j++) { if (matrix[i][j] < 0) { matrix[i][j] = MAX_VALUE / 3; } if (i != j) { addEdge(i, j, matrix[i][j]); addEdge2(j, i, matrix[i][j]); } } } //存储节点介数 double[] betweeness = new double[n]; for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { if (i!=j){ se = new ArrayList<>(); //起点到终点 s = i; t = j; //调用dijstra算法计算最短路径 dijstra(s); System.out.println("The least distance from " + s + "->" + t + " is " + dis[t]); List<Integer> vec = new ArrayList<>(); prinPath(t, vec); System.out.println("最短路径有:" + se.size() + "条"); for (List<Integer> ans : se) { for (int k = ans.size() - 1; k>0; k--) { System.out.print(ans.get(k) + "->"); } System.out.println(ans.get(0)); } for (List<Integer> ans : se) { for (Integer an : ans) { if (an != s && an != t) { betweeness[an] = ArithUtil.add(betweeness[an], ArithUtil.div(1,se.size())); } } } } } } return betweeness; } }
测试:
public static void main(String[] args) { /* double[][] matrix = {{0, 5, 2, 6,-1}, {-1,0,-1,-1 ,1}, {-1, 1, 0, 3,5}, {-1,-1,-1, 0,2}, {-1,-1,-1,-1,0}};*/ double[][] matrix = new double[][]{ {0, 1, -1, 1, -1, -1}, {1, 0, 1, -1, 1, -1}, {-1, 1, 0, -1, -1, 1}, {1, -1, -1, 0, 1, -1}, {-1, 1, -1, 1, 0, 1}, {-1, -1, 1, -1, 1, 0} }; double[] doubles = Betweeness.calculateBetweeness(matrix); System.out.println(Arrays.toString(doubles)); }
附:
测试方法中的图模型:
1:
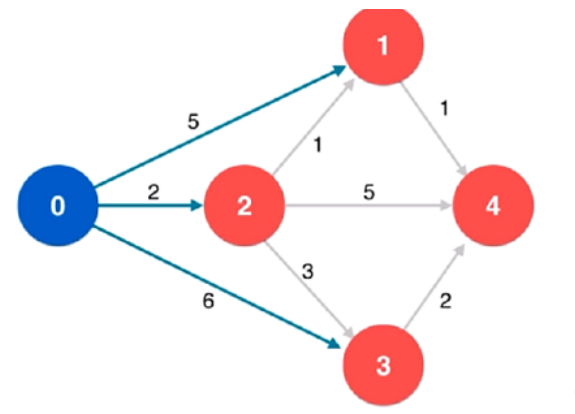
2:
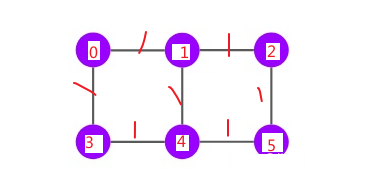
心有所想,必有回响



