[时间序列分析]--平稳性,白噪声的检验
使用mathematica来实现。
做时间序列分析，之前需要做两个准备工作，即检查序列是否是平稳的，如果是平稳的，还要检查是否是白噪声。我们一个一个来讲。
使用数据
我们用一个例子来说明：数据集是49 - 98 北京最高气温，数据如下：
{{1949., 38.8}, {1950., 35.6}, {1951., 38.3}, {1952., 39.6}, {1953.,
37.}, {1954., 33.4}, {1955., 39.6}, {1956., 34.6}, {1957.,
36.2}, {1958., 37.6}, {1959., 36.8}, {1960., 38.1}, {1961.,
40.6}, {1962., 37.1}, {1963., 39.}, {1964., 37.5}, {1965.,
38.5}, {1966., 37.5}, {1967., 35.8}, {1968., 40.1}, {1969.,
35.9}, {1970., 35.3}, {1971., 35.2}, {1972., 39.5}, {1973.,
37.5}, {1974., 35.8}, {1975., 38.4}, {1976., 35.}, {1977.,
34.1}, {1978., 37.5}, {1979., 35.9}, {1980., 35.1}, {1981.,
38.1}, {1982., 37.3}, {1983., 37.2}, {1984., 36.1}, {1985.,
35.1}, {1986., 38.5}, {1987., 36.1}, {1988., 38.1}, {1989.,
35.8}, {1990., 37.5}, {1991., 35.7}, {1992., 37.5}, {1993.,
35.8}, {1994., 37.2}, {1995., 35.}, {1996., 36.}, {1997.,
38.2}, {1998., 37.2}}
一.
画出散点图(时序图)
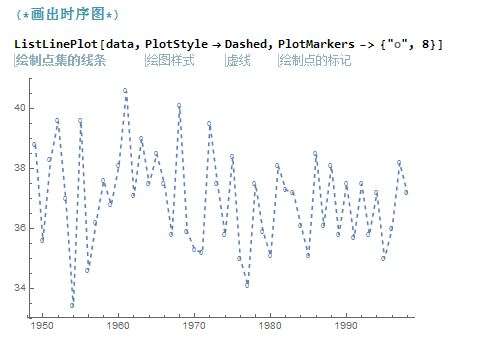
首先我们画出散点图，先从总体上看一下数据
-
ListLinePlot[data, PlotStyle -> Dashed, PlotMarkers -> {"o", 8}]
二.
平稳性的检验
方法：平稳性检验一般可以从时序图上看或者通过相关性的图中看出。
我们这里讲一下相关图的方法。
原理：平稳序列通常具有短期相关性。该性质用自相关系数来描述就是随着延迟期数的增加，平稳序列的自相关系数会很快的衰减到0
特别，关于延迟的相关系数的计算公式如下
在mathematica里使用的函数是CorrelationFunction[]，具体代码如下
ListPlot[
CorrelationFunction[Table[x[i], {i, 1, 100}], {20}],
PlotMarkers -> {Automatic, Medium}, Filling -> Axis,
FillingStyle -> Directive[Thickness[.01], Green, Dashed],
PlotRange -> All
] 
可以看到相关系数迅速衰减到0，说明该序列是平稳的。
上面说的相对平稳其实是凭直觉的，下面讲一个稍微好一点的方法。
这里要用到下面的Barlett定理，可以先看一下 三.判断数据是否是白噪声 的那张图，由于p服从N[0,1/n]的正态分布，故我们可以考虑算出其95%的置信区间。
pacf[data_, lmax_, clev_: 0.95] :=
Show[ListPlot[CorrelationFunction[data, {lmax}], Filling -> Axis,
PlotRange -> {{0, lmax}, {-1.5, 1.5}},
PlotStyle -> PointSize[Medium]],
Graphics[{Dashed, Line[{{0, #}, {lmax, #}}]}] & /@ (
Quantile[NormalDistribution[], {(1 - clev)/2, 1 - (1 - clev)/2}]/
Sqrt[Length[data]])]
我们看一下效果：
可以看到除了第一个点，那个不算，因为他是滞后为0，所以相关系数为1。后面的点都在95%的置信区间里面。这样只要后面的点不会在超出这个置信区间，就可以认为其是衰减到0的。
三.
判断数据是否是白噪声
如果一个序列是平稳的，那么下面我们就要判断数据是否是白噪声，白噪声没有研究的意义。
在mathematica中，判断白噪声使用AutocorrelationTest[]，这个函数
这个函数必须要说明一下，首先他的原理是bartlett定理
下面对于AutocorrelationTest[]这个函数的使用进行说明，如下图：
她返回的是一个p值，p值越大表示原假设成立的可能性越大，即数据是随机的可能性越大。
即p值越大，随机的可能性越大
-
ListPlot[Table[AutocorrelationTest[data[[All, 2]], i], {i, 1, 10}], Filling -> Axis]
我们可以画出关于滞后数的图
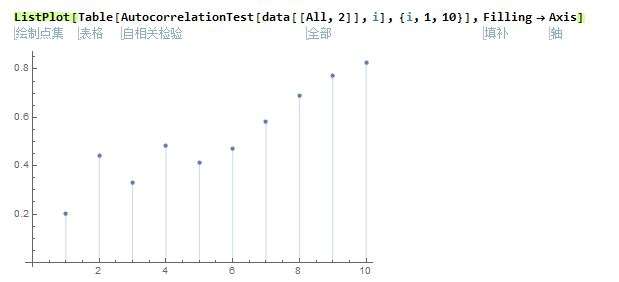我们可以看到p值还是挺大的，所以认为该数据是白噪声。
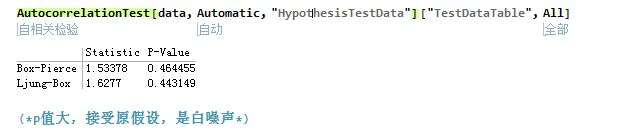
我们还有一些其他的检验方法，如下图
-
AutocorrelationTest[data, Automatic, "HypothesisTestData"]["TestDataTable", All]
也可以使用下图的方式
以上就把白噪声的检验做完了。
