线段树

求最大值

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define endl "\n"
//转换成斜率，画图知斜率最大一定是出现在相邻两点之间
//太妙了
const int N = 2e5 + 5;
int a[N];
ll Tree[N * 4];
void build(int now, int l, int r) {
    if (l == r) {
        Tree[now] = a[l] - a[l - 1];
        return;
    }
    int mid = (l + r) >> 1;
    build(now * 2, l, mid);
    build(now * 2 + 1, mid + 1, r);
    Tree[now] = max(Tree[now * 2], Tree[now * 2 + 1]);
}
void modify(int now, int l, int r, int pos, int v) {
    if (l == r) {
        Tree[now] = v;
        return;
    }
    int mid = (l + r) >> 1;
    if (pos <= mid)modify(now * 2, l, mid, pos, v);
    else modify(now * 2 + 1, mid + 1, r, pos, v);
    Tree[now] = max(Tree[now * 2], Tree[now * 2 + 1]);
}
int main()
{
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    int n;
    while(cin>>n){
    for (int i = 1; i <= n; i++)cin >> a[i];
        build(1, 2, n);
        int T = 1;
        cin >> T;
        while (T--) {
            int x, y;
            cin >> x >> y;
            a[x] = y;
            if (x > 1)modify(1, 2, n, x, a[x] - a[x - 1]);
            if (x < n)modify(1, 2, n, x + 1, a[x + 1] - a[x]);
            double ans = Tree[1];
            cout << fixed << setprecision(2) << ans << endl;
        }
    }
    return 0;
}

Light Switching

当区间只有01两种状态时，使用异或操作，lazy标记也用异或操作实现

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define endl "\n"
const int N = 1e5 + 5;
struct TreeNode {
    int sum, ok;
}Tree[4*N];
void pushdown(int now,int l,int r) {
    int mid = (l + r) >> 1;
    Tree[now * 2].sum = mid - l + 1 - Tree[now*2].sum;
    Tree[now * 2 + 1].sum = r - mid - Tree[now*2+1].sum;
    Tree[now * 2].ok ^= 1; Tree[now * 2 + 1].ok ^= 1;
    Tree[now].ok = 0;
}
void pushup(int now) {
    Tree[now].sum = Tree[now * 2].sum + Tree[now * 2 + 1].sum;
}
void modify(int now, int l, int r, int x, int y) {
    if (x <= l && y >= r) {
        Tree[now].ok ^= 1;
        Tree[now].sum = r - l + 1 - Tree[now].sum;
        return;
    }
    int mid = (l + r) >> 1;
    if(Tree[now].ok)pushdown(now, l, r);
    if (x <= mid)modify(now * 2, l, mid, x, y);
    if (y > mid)modify(now * 2 + 1, mid + 1, r, x, y);
    pushup(now);
}
ll qurey(int now, int l, int r, int x, int y) {
    if (x <= l && y >= r)return Tree[now].sum;
    if(Tree[now].ok)pushdown(now, l, r);
    int mid = (l + r) >> 1;
    ll res = 0;
    if (x <= mid)res += qurey(now * 2, l, mid, x, y);
    if (y > mid)res += qurey(now * 2 + 1, mid + 1, r, x, y);
    pushup(now);
    return res;
}
int main()
{
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    int n, m;
    cin >> n >> m;
    while (m--) {
        int op;
        cin >> op;
        if (op == 1) {
            int x, y;
            cin >> x >> y;
            cout << qurey(1, 1, n, x, y) << endl;
        }
        else {
            int x, y;
            cin >> x >> y;
            modify(1, 1, n, x, y);
        }
    }
    return 0;
}

  红球进黑洞

异或操作无法通过公式展开，对二进制每一位开一个线段树，求和就是将所有元素对每一位的1的个数乘上对应2的n次方求和

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define endl "\n"
//二维线段树，对二进制每一位开一个线段树，这样就可以用lazy优化异或操作

const int N = 1e5 + 5;
int a[N];

struct TreeNode {
    ll sum, ok;
}Tree[N * 4][25];

void pushup(int now, int now_bit) {
    Tree[now][now_bit].sum = Tree[now * 2][now_bit].sum + Tree[now * 2 + 1][now_bit].sum;
}
//Tree[now][now_bit].ok为1才pushdown，为1代表之前已经修改过了，这是pushdown下传信息，再去修改或者询问，用的时候再pushdown，这样子优化

void pushdown(int now, int now_bit, int l, int r) {
    //不能直接这样子写，因为可能之前就有标记，如果之前有标记，再打标记相当于什么都不做
    //Tree[now * 2][now_bit].ok = Tree[now * 2 + 1][now_bit].ok = 1;
    int mid = (l + r) >> 1;
    Tree[now * 2][now_bit].sum = mid - l + 1 - Tree[now * 2][now_bit].sum;
    Tree[now * 2 + 1][now_bit].sum = r - mid - Tree[now * 2 + 1][now_bit].sum;
    Tree[now * 2][now_bit].ok ^= 1; Tree[now * 2 + 1][now_bit].ok ^= 1;
    Tree[now][now_bit].ok = 0;
}
void build(int now, int now_bit, int l, int r) {
    if (l == r) {
        Tree[now][now_bit].sum = ((a[l] >> now_bit) & 1);
        return;
    }
    int mid = (l + r) >> 1;
    build(now * 2, now_bit, l, mid);
    build(now * 2 + 1, now_bit, mid + 1, r);
    pushup(now, now_bit);
}
ll qurey(int now, int now_bit, int l, int r, int x, int y) {
    if (l >= x && r <= y)return Tree[now][now_bit].sum;
    if (Tree[now][now_bit].ok)pushdown(now, now_bit, l, r);
    int mid = (l + r) >> 1;
    ll res = 0;
    if (x <= mid)res += qurey(now * 2, now_bit, l, mid, x, y);
    if (y > mid)res += qurey(now * 2 + 1, now_bit, mid + 1, r, x, y);
    return res;
}
void modify(int now, int now_bit, int l, int r, int x, int y) {
    if (l >= x && r <= y) {
        Tree[now][now_bit].sum = r - l + 1 - Tree[now][now_bit].sum;
        Tree[now][now_bit].ok ^= 1;
        return;
    }
    if (Tree[now][now_bit].ok)pushdown(now, now_bit, l, r);
    int mid = (l + r) >> 1;
    if (x <= mid)modify(now * 2, now_bit, l, mid, x, y);
    if (y > mid)modify(now * 2 + 1, now_bit, mid + 1, r, x, y);
    pushup(now, now_bit);
}

int main()
{
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++)cin >> a[i];
    for (int i = 0; i <= 20; i++)build(1, i, 1, n);
    while (m--) {
        int op;
        cin >> op;
        if (op == 1) {
            int x, y;
            cin >> x >> y;
            ll res = 0;
            for (int i = 0; i <= 20; i++) {
                res += qurey(1, i, 1, n, x, y) * (1LL << i);
            }
            cout << res << endl;
        }
        else {
            int x, y, k;
            cin >> x >> y >> k;
            for (int i = 0; i <= 20; i++) {
                if ((k >> i) & 1)modify(1, i, 1, n, x, y);
            }
        }
    }
    return 0;
}

践踏

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define endl "\n"

//一个区间最不管长度多长，都只能对取模后的l，r产生1的贡献值，因为op==3时询问的是有多少个区间
//通过unique和erase离散化建立线段树

const int N = 1e5 + 5;
vector<int>vec;
struct Node {
    int op, l, r, x;
}a[N];

struct BIT {
    int c[4 * N];
    void modify(int x, int k) {
        for (; x <= N; x += x & (-x)) {
            c[x] += k;
        }
    }
    int qurey(int x) {
        int ans = 0;
        for (; x; x -= x & (-x)) {
            ans += c[x];
        }
        return ans;
    }
}Tree;

//获得离散后x是第几大的
int get_idx(int x) {
    return lower_bound(vec.begin(), vec.end(), x) - vec.begin() + 1;
}

int main() {
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    int n, k;
    cin >> n >> k;
    if (n == 0) { cout << "fafa"; return 0; }
    for (int i = 1; i <= n; i++) {
        cin >> a[i].op;
        if (a[i].op == 1) {
            cin >> a[i].l >> a[i].r;
            vec.push_back(a[i].l); vec.push_back(a[i].r);
        }
        else if (a[i].op == 2) {
            cin >> a[i].l >> a[i].r;
            vec.push_back(a[i].l); vec.push_back(a[i].r);
        }
        else {
            cin >> a[i].x;
            //这里需要push_back当前x的值
            //不然离散化后不会被覆盖到
            vec.push_back(a[i].x);
        }
    }
    //离散化
    sort(vec.begin(), vec.end());
    vec.erase(unique(vec.begin(), vec.end()), vec.end());

    if (k == 0) {
        for (int i = 1; i <= n; i++) {
            if (a[i].op == 1) {
                int l = get_idx(a[i].l); int r = get_idx(a[i].r);
                Tree.modify(l, 1); Tree.modify(r + 1, -1);
            }
            else if (a[i].op == 2) {
                int l = get_idx(a[i].l); int r = get_idx(a[i].r);
                Tree.modify(l, -1); Tree.modify(r + 1, 1);
            }
            else {
                int ans = get_idx(a[i].x);
                cout << Tree.qurey(ans) << endl;
            }
        }
    }
    else {
        for (int i = 1; i <= n; i++) {
            if (a[i].op == 1) {
                int len = a[i].r - a[i].l + 1;
                if (len >= k) {
                    Tree.modify(1, 1);
                    Tree.modify(k + 1, -1);
                }
                else {
                    int mod_l = a[i].l % k + 1;
                    int mod_r = a[i].r % k + 1;
                    if (mod_l <= mod_r) {
                        Tree.modify(mod_l, 1);
                        Tree.modify(mod_r + 1, -1);
                    }
                    else {
                        Tree.modify(1, 1);
                        Tree.modify(mod_r + 1, -1);
                        Tree.modify(mod_l, 1);
                        Tree.modify(k + 1, -1);
                    }
                }
            }
            else if (a[i].op == 2) {
                int len = a[i].r - a[i].l + 1;
                if (len >= k) {
                    Tree.modify(1, -1);
                    Tree.modify(k + 1, 1);
                }
                else {
                    int mod_l = a[i].l % k + 1;
                    int mod_r = a[i].r % k + 1;
                    if (mod_l <= mod_r) {
                        Tree.modify(mod_l, -1);
                        Tree.modify(mod_r + 1, 1);
                    }
                    else {
                        Tree.modify(1, -1);
                        Tree.modify(mod_r + 1, 1);
                        Tree.modify(mod_l, -1);
                        Tree.modify(k + 1, 1);
                    }
                }
            }
            else {
                cout << Tree.qurey(a[i].x % k + 1) << endl;
            }
        }
    }
    return 0;
}

H-0 and 1 in BIT

 op1-->-x-1

op2-->x+1

由线性代数知识推每次操作要乘的矩阵，线段树维护一个矩阵信息

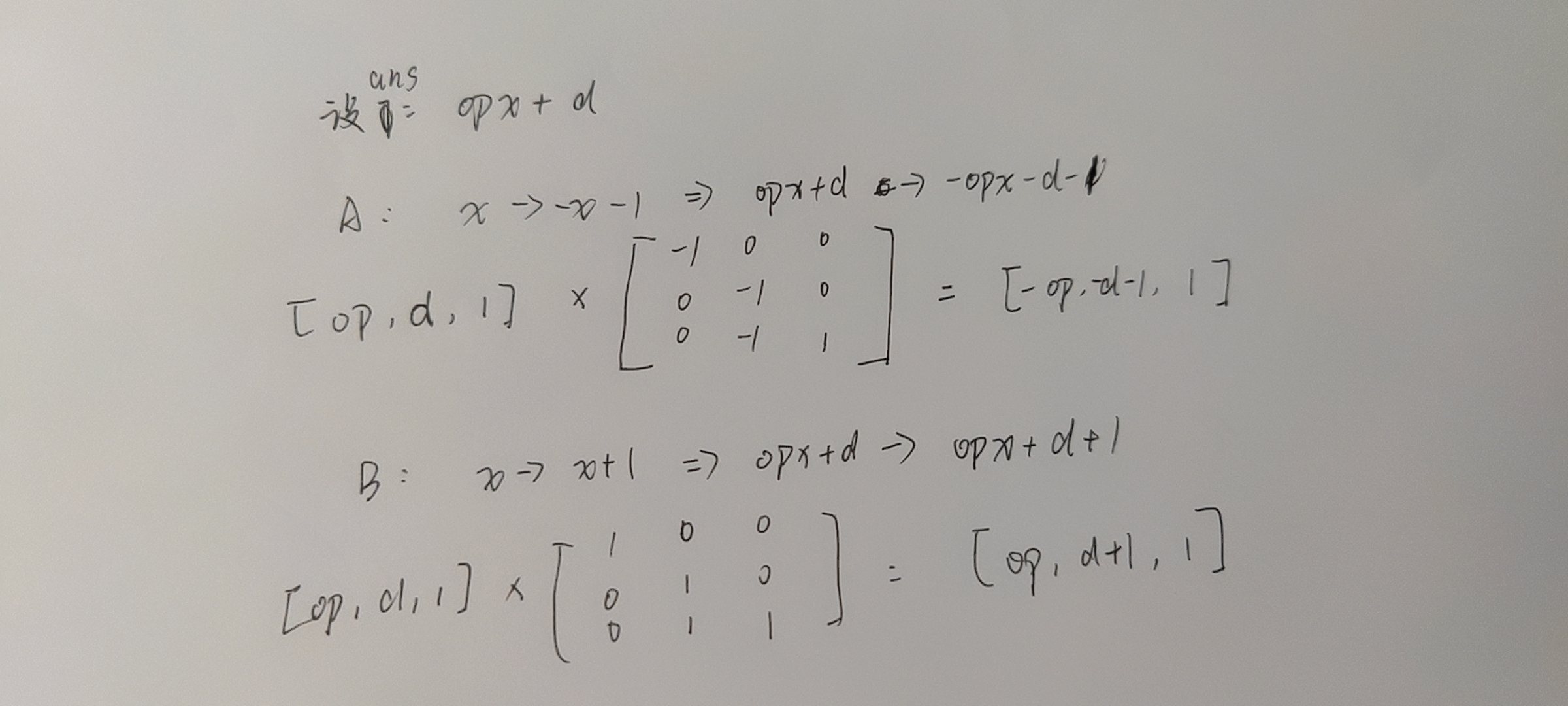
 [op,d,1] 就是代表一个f(x)=kx+b的方程，根据线性代数知识用矩阵表示该方程 -> f(x)=op*x+d , 最后一个1只是凑矩阵用的 ，f代表该矩阵，因为刚开始就是x，所以op=1，d=0

#include<bits/stdc++.h>
using namespace std;
#define endl "\n"
typedef long long ll;

const int sz=3;
const int N=2e5+5;

string s;

struct mat {
  ll m[sz][sz];
  mat() { memset(m, 0, sizeof m); }
  mat operator-(const mat& T) const {
    mat res;
    for (int i = 0; i < sz; ++i)
      for (int j = 0; j < sz; ++j) {
        res.m[i][j] = (m[i][j] - T.m[i][j]);
      }
    return res;
  }
  mat operator+(const mat& T) const {
    mat res;
    for (int i = 0; i < sz; ++i)
      for (int j = 0; j < sz; ++j) {
        res.m[i][j] = (m[i][j] + T.m[i][j]);
      }
    return res;
  }
  mat operator*(const mat& T) const {
    mat res;
    int r;
    for (int i = 0; i < sz; ++i)
      for (int k = 0; k < sz; ++k) {
        r = m[i][k];
        for (int j = 0; j < sz; ++j)
          res.m[i][j] += T.m[k][j] * r ;
      }
    return res;
  }
  mat operator^(ll x) const {
    mat res, bas;
    for (int i = 0; i < sz; ++i) res.m[i][i] = 1;
    for (int i = 0; i < sz; ++i)
      for (int j = 0; j < sz; ++j) bas.m[i][j] = m[i][j];
    while (x) {
      if (x & 1) res = res * bas;
      bas = bas * bas;
      x >>= 1;
    }
    return res;
  }
}A,B,f,Tree[4*N],unit;

void build(int now,int l,int r){
    if(l==r){
        if(s[l-1]=='A')Tree[now]=A;
        else Tree[now]=B;
        return;
    }
    int mid=(l+r)>>1;
    build(now*2,l,mid);
    build(now*2+1,mid+1,r);
    Tree[now]=Tree[now*2]*Tree[now*2+1];
}

mat qurey(int now,int l,int r,int x,int y){
    if(x<=l&&y>=r)return Tree[now];
    int mid=(l+r)>>1;
    mat ans=unit;
    if(x<=mid)ans=ans*qurey(now*2,l,mid,x,y);
    if(y>mid)ans=ans*qurey(now*2+1,mid+1,r,x,y);
    return ans;
}

int main(){
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    int n,q;cin>>n>>q>>s;
    int last=0;
    A.m[0][0]=A.m[1][1]=A.m[2][1]=-1;
    A.m[2][2]=B.m[2][1]=1;
    f.m[0][0]=f.m[0][2]=1;
    for(int i=0;i<3;i++)B.m[i][i]=1,unit.m[i][i]=1;
    build(1,1,n);
    while(q--){
        int l,r;cin>>l>>r;
        string now;cin>>now;
        int rl=(last^l)%n+1,rr=(last^r)%n+1;
        l=min(rl,rr);r=max(rl,rr);
        mat calc=f*qurey(1,1,n,l,r);
        ll len=now.size(),t=0;
        for(int i=0;i<len;i++)t=t*2+(now[i]-'0');
        ll mod=1ll<<len;
        last=((t*calc.m[0][0]%mod+mod)%mod+calc.m[0][1]%mod+mod)%mod;
        for(int i=len-1;i>=0;i--){
            if((last>>i)&1)cout<<1;
            else cout<<0;
        }
        cout<<endl;
        if(last<0)break;
    }

    return 0;
}