泰勒展开

一般取x0=0时即可用多项式拟合某函数

CODECHEF APRIL18 CHEFAT

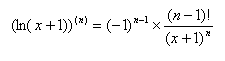
所以

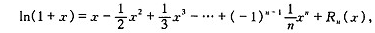
线段树维护多项式。由于x<0.9，可以取较小的n得到较好的拟合效果

#include <cstdio>
#include <iostream>
#include <cmath>
#define LDB double
using namespace std;

  const int lim=120;
  int cnt,n,q;
  LDB p[200001];

  struct treenode{
      int l,r,lc,rc;
      LDB toadd,poly[lim+10];
      
      void taylor(LDB num){
        LDB p=1;
      for (int i=1;i<=lim;i++){
          p*=num;
          poly[i]=-p/i;
      }
    }
  }tr[200001];

  void pushdown(int po){
      if (fabs(tr[po].toadd-1)>1e-9){
        LDB p=1;
      for (int i=1;i<=lim;i++){
          p*=tr[po].toadd;
          tr[po].poly[i]*=p;
      }    
      tr[tr[po].lc].toadd*=tr[po].toadd;
      tr[tr[po].rc].toadd*=tr[po].toadd;
      tr[po].toadd=1;
    }
  }

  void update(int po){
      pushdown(po);
      LDB p1=1,p2=1;
      for (int i=1;i<=lim;i++){
        p1*=tr[tr[po].lc].toadd;p2*=tr[tr[po].rc].toadd;
        tr[po].poly[i]=tr[tr[po].lc].poly[i]*p1+tr[tr[po].rc].poly[i]*p2;    
    }
  }

  void build(int l,int r){
      tr[++cnt].l=l;tr[cnt].r=r;tr[cnt].toadd=1;
      if (l==r){
        tr[cnt].taylor(p[l]);
      return;    
    }
    
    int mid=(l+r)>>1,t=cnt;
    tr[t].lc=cnt+1;build(l,mid);
    tr[t].rc=cnt+1;build(mid+1,r);
    update(t);
  }

  LDB que(int po,int l,int r){
      pushdown(po);
      if (tr[po].l==l&&tr[po].r==r){
        LDB ret=0;
      for (int i=1;i<=lim;i++) ret+=tr[po].poly[i];
      return(ret);    
    }
    
    LDB ret=0;
    int mid=(tr[po].l+tr[po].r)>>1;
    if (l<=mid) ret+=que(tr[po].lc,l,min(mid,r));
    if (r>mid)  ret+=que(tr[po].rc,max(mid+1,l),r);
    return(ret);
  }
  
  void edi(int po,int l,int r,LDB num){
      pushdown(po);
      if (tr[po].l==l&&tr[po].r==r){
        tr[po].toadd*=num;return;    
    }
    
    int mid=(tr[po].l+tr[po].r)>>1;
    if (l<=mid) edi(tr[po].lc,l,min(mid,r),num);
    if (r>mid)  edi(tr[po].rc,max(mid+1,l),r,num);
    update(po); 
  }

  int main(){
      scanf("%d%d",&n,&q);
      for (int i=1;i<=n;i++) scanf("%lf",&p[i]);
      build(1,n);
      
      for (int i=1;i<=q;i++){
        int opt,t1,t2;LDB t3;
        scanf("%d%d%d",&opt,&t1,&t2);
      if (opt==0){
          LDB t=que(1,t1,t2);
          printf("%.9lf\n",exp(t));
      }else{
        scanf("%lf",&t3);
        edi(1,t1,t2,t3);
      }
    }
  }