CC科技
区间不重的ST表 https://discuss.codechef.com/questions/116821/segprod-editorial
$\sum\limits_{i=0}^\infty \dfrac{x^i}{i!}=e^x$ so inverse series for it is $e^{-x}=\sum\limits_{i=0}^\infty \dfrac{(-x)^i}{i!}$
将以$D^k$为变量的多项式替换为$D^{(k)}=\prod\limits_{i=1}^{k}(D+i)$的多项式。
https://discuss.codechef.com/questions/117004/binomsum-editorial
对于某个排列P,P的逆序对数是K。则对于P的任意区间所包含的数，权值构成的连续区间数不超过sqrt(k)
https://discuss.codechef.com/questions/91627/how-to-solve-seainvs
$A*B$ = $(x_{1}^2+x_{2}^2+x_{3}^2+x_{4}^2)*(y_{1}^2+y_{2}^2+y_{3}^2+y_{4}^2)$ =
$(x_{1}*y_{1}+x_{2}*y_{2}+x_{3}*y_{3}+x_{4}*y_{4})^2 + $
$(x_{1}*y_{2}-x_{2}*y_{1}+x_{3}*y_{4}-x_{4}*y_{3})^2 + $
$(x_{1}*y_{3}-x_{2}*y_{4}-x_{3}*y_{1}+x_{4}*y_{2})^2 + $
$(x_{1}*y_{4}-x_{4}*y_{1}+x_{2}*y_{3}-x_{2}*y_{3})^2 $
https://discuss.codechef.com/questions/90269/foursq-editorial
Lindström–Gessel–Viennot lemma
对于一张无边权的DAG图，给定n个起点和对应的n个终点，这n条不相交路径的方案数为
det(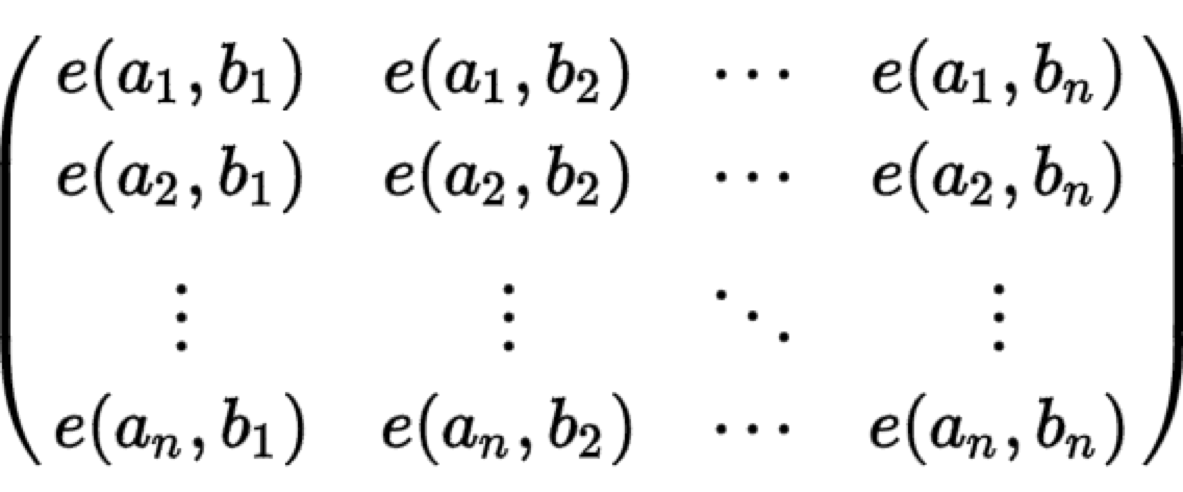
) （该矩阵的行列式）
其中e(a,b)为图上a到b的方案数
https://discuss.codechef.com/questions/80665/chnbgmt-editorial
通过函数值检验函数是否存在k阶线性递推
求
\begin{vmatrix}
f[1] & f[2] & \dots & f[k]\\
f[2] & f[3] & \dots & f[k+1] \\
\dots & \dots & \ddots & \dots \\
f[k] & f[k+1] & \dots & f[k+k-1]
\end{vmatrix}
若为0则为k-1阶线性递推
https://discuss.codechef.com/questions/78427/dmcs-editorial
$(n+1) {\rm lcm} ({n \choose 0}, {n \choose 1}, \dots {n \choose k}) = {\rm lcm} (n+1,n,n-1, \dots n+1-k)$
http://discuss.codechef.com/problems/LOTERY
求翻转后的FFT结果
$B(x) = B_{0} + B_{1}x + B_{2}x^2 + ... B_{L-1}x^{L-1} $
$ =A_{L-1} + A_{L-2}x + A_{L-3}x^2 + ... + A_{0}x^{L-1} $
$ =x^{L-1} (A_{L-1}x^{-(L-1)} + A_{L-2}x^{-(L-2)} + ... + A_{0}) $
$ =x^{L-1} A(x^{-1}) $
$ =x^{L-1} A(1/x)$
https://discuss.codechef.com/questions/74772/mgch3d-editorial
求区间内不重复数时考虑每个数上次出现的位置转为二维数点
https://discuss.codechef.com/questions/74081/distnum-editorial
笛卡尔定理，圆反演
https://discuss.codechef.com/questions/72678/nthcir-editorial
最大可平面图（不会）
https://discuss.codechef.com/questions/71547/conpoin-editorial
霍尔定理推广， In a bipartite graph with $N$ vertices on the left side, the maximum value of $(\| S \| - \| N(S) \|)$, $S$ being a subset of left side vertices, will be $(N - k)$, where $k$ is the size of the maximum matching
https://discuss.codechef.com/questions/69002/sez-editorial
gcd(a, b, c, d..) = gcd(a, b-a, c-b, d-c...)支持区间加操作
https://discuss.codechef.com/questions/1588/dgcd-editorial
treap中求两节点间距离
https://discuss.codechef.com/questions/38704/cot5-editorial
Hall system及其转移
https://discuss.codechef.com/questions/1131/match-editorial
sin(mX)=2cos(X)sin((m − 1))−sin((m − 2)X)，所以有sin(k*X)的二阶线性递推
https://s3.amazonaws.com/codechef_shared/download/PARSIN.pdf
pisano period.斐波那契额数列在模n的意义下有π(n)大小的循环节
https://discuss.codechef.com/questions/49338/sigfib-editorial
在$o(nlogn)$时间内将树的所有子树与子树外0,1染色
https://discuss.codechef.com/questions/127265/edgest-editorial
