类欧几里得算法

f(a,b,c,n)=∑⌊（ai+b）/c⌋，即求直线下的整点个数

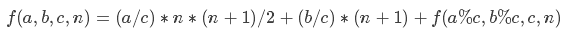
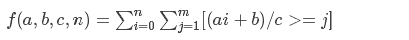
  LL work(LL a,LL b,LL c,LL n){
      LL ret=n*(n+1)/2*(a/c)+(b/c)*(n+1);
      a%=c;b%=c;
      if (!a) return(ret);else{
        LL m=(a*n+b)/c;
      ret+=n*m;
      ret-=work(c,c-b-1,a,m-1);
    }
    return(ret);
  }

 ---------------------------------------------------------------------------------------------

以上算法能够快速求出直线下方（包括直线上的）纵坐标大于0，横坐标大于等于0的点的数量

而在一些问题中还需要用到所有点的横坐标之和(记为g)，以及每个横坐标上点的数量的平方的和(记为g)

当a>=c||b>=c时，可以将a,b通过计算贡献后对c取模缩小范围。

否则

对于g来说。每个纵坐标上的函数值是一个等差序列。拆开等差序列求和的式子后可以递归计算。

对于h可以将n^2分解为

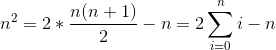
同样可以计算。

具体推导过程可见 http://blog.csdn.net/werkeytom_ftd/article/details/53812718

  data likegcd(LL a,LL b,LL c,LL n){
      data ret;ret.f=ret.g=ret.h=0;
      LL N=n%mo,N_N1=N*(N+1)%mo,N_N1_2N1=N%mo*(N+1)%mo*(2*N+1)%mo;
      if (a==0) return(ret);
      if (a>=c||b>=c){
        LL N_N1_inv2=N_N1*inv2%mo,N_N1_2N1_inv6=N_N1_2N1*inv6%mo;
        data t=likegcd(a%c,b%c,c,n);    
        ret.f+=t.f+a/c*N_N1_inv2%mo+b/c*(N+1)%mo;ret.f%=mo;
        ret.g+=t.g+a/c*N_N1_2N1_inv6%mo+(b/c)*N_N1_inv2%mo;ret.g%=mo;
        ret.h+=(a/c)*(a/c)%mo*N_N1_2N1_inv6%mo+
               (b/c)*(b/c)%mo*(N+1)%mo+
               (a/c)*(b/c)%mo*N_N1%mo+
               t.h+
               2*(a/c)%mo*t.g%mo+
               2*(b/c)%mo*t.f%mo;
      ret.h%=mo;
      return(ret);               
    }else{
      LL m=(a*n+b)/c,M=m%mo;
      data t=likegcd(c,c-b-1,a,m-1);      
      ret.f=N*M%mo-t.f;ret.f%=mo;
      ret.g=(N_N1%mo*M%mo-t.f-t.h)%mo*inv2%mo;ret.g%=mo;
      ret.h=N*M%mo*(M+1)%mo-2*t.g-2*t.f-ret.f;ret.h%=mo;
      return(ret);
    }
  }