算法设计与分析之动态规划
今天刚刚学了动态规划,把书上的代码敲了一下,在此留下一笔。动态规划与分治法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。在子问题的求解过程中,有很多子问题被重复计算了。于是我们可以用一个表来记录所有已解决的子问题的的答案。不管该问题以后是否被用到,只要它被计算过,就将其结果填入表中。这就是动态规划的基本思想。
一、动态规划的设计步骤:
(1)找出最优解的性质,并刻画其结构特征;
(2)递归地定义最优值;
(3)以自顶向下的方式计算出最优值;
(4)根据计算最优值时得到的信息,构造最优解。
下面使用动态规划来解决的是矩阵连乘问题。
问题描述:给定n个矩阵:A1,A2,...,An,其中Ai与Ai+1是可乘的,i=1,2...,n-1。确定计算矩阵连乘积的计算次序,使得依此次序计算矩阵连乘积需要的数乘次数最少。输入数据为矩阵个数和每个矩阵规模,输出结果为计算矩阵连乘积的计算次序和最少数乘次数。
第一步分析最优解的结构:
若将对应m[i][j]的断开位置k记为s[i][j],在计算出最优值m[i][j]后,可递归地由s[i][j]构造出相应的最优解。s[i][j]中的数表明,计算矩阵链A[i:j]的最佳方式应在矩阵Ak和Ak+1之间断开,即最优的加括号方式应为(A[i:k])(A[k+1:j)。因此,从s[1][n]记录的信息可知计算A[1:n]的最优加括号方式为(A[1:s[1][n]])(A[s[1][n]+1:n]),进一步递推,A[1:s[1][n]]的最优加括号方式为(A[1:s[1][s[1][n]]])(A[s[1][s[1][n]]+1:s[1][s[1][n]]])。同理可以确定A[s[1][n]+1:n]的最优加括号方式在s[s[1][n]+1][n]处断开...照此递推下去,最终可以确定A[1:n]的最优完全加括号方式,及构造出问题的一个最优解。
第二步、建立递归关系
设计算A[i:j],1≤i≤j≤n,所需要的最少数乘次数m[i,j],则原问题的最优值为m[1,n]。
当i=j时,A[i:j]=Ai,因此,m[i][i]=0,i=1,2,…,n
当i<j时,若A[i:j]的最优次序在Ak和Ak+1之间断开,i<=k<j,则:m[i][j]=m[i][k]+m[k+1][j]+pi-1pkpj。由于在计算是并不知道断开点k的位置,所以k还未定。不过k的位置只有j-i个可能。因此,k是这j-i个位置使计算量达到最小的那个位置。
综上,有递推关系如下:
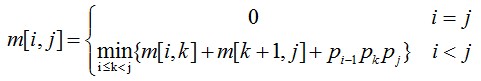
第三步、计算最优解
最后代码如下:
package algo.chapter3; import java.io.Serializable; /** * 矩阵相乘 * @author Administrator * */ public class MatrixPlus { public static void matrixChain(int[] p,int [][]m,int [][]s) { int n = p.length-1; for(int i=1;i<=n;i++) m[i][i] = 0; for(int r=2;r<=n;r++) //对角线上循环的次数 for(int i=1;i<=n-r+1;i++) { int j = i+r-1; m[i][j] = m[i+1][j] + p[i-1]*p[i]*p[j]; s[i][j] = i; for(int k=i+1;k<j;k++) { int t = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j]; if(t < m[i][j]) { m[i][j] = t; //递归式,记录k的位置 s[i][j] = k; } } } } public static void traceback(int [][]s,int i,int j) { if(i == j) return; traceback(s,i,s[i][j]); traceback(s,s[i][j]+1,j); System.out.println("Multiply A"+i+"."+s[i][j]+ "and A"+(s[i][j]+1)+"."+j); } //打印加括号的最优解方案 public static void optimalParens(int [][]s,int i,int j) { if(i==j) System.out.print("(A"+i); else { optimalParens(s,i,s[i][j]); optimalParens(s,s[i][j]+1,j); System.out.print(")"); } } }
测试代码:
package algo.chapter3.test; import algo.chapter3.MatrixPlus; public class MatrixTest { public static void main(String[] args) { // TODO Auto-generated method stub int [] p = {39,45,35,15,23,45,67,10,26,37}; int n = p.length; //{{12,3,45,56},{2,4,6,23},{9,87,34,23},{23,45,56,56},{23,3,6,8}} int [][] m = new int[n][n]; int [][] s = new int[n][n]; MatrixPlus.matrixChain(p, m, s); System.out.println("该矩阵阶乘子问题数乘的个数为:"); for(int i=1;i<m.length;i++) { for(int j=1;j<m.length;j++) { if(i>j) { System.out.print("----"+"\t"); } else { System.out.print(m[i][j]+"\t"); } } System.out.println(); } System.out.println(); System.out.println("该矩阵阶乘子问题数乘的个数为:"); for(int i=1;i<s.length;i++) { for(int j=1;j<s.length;j++) { if(i>j) { System.out.print("----"+"\t"); } else { System.out.print(s[i][j]+"\t"); } } System.out.println(); } System.out.println(); System.out.println("该矩阵阶乘的最优解为:"); MatrixPlus.traceback(s, 1, n-1); MatrixPlus.optimalParens(s, 1, n-1); } }
最后的运行结果如下图:
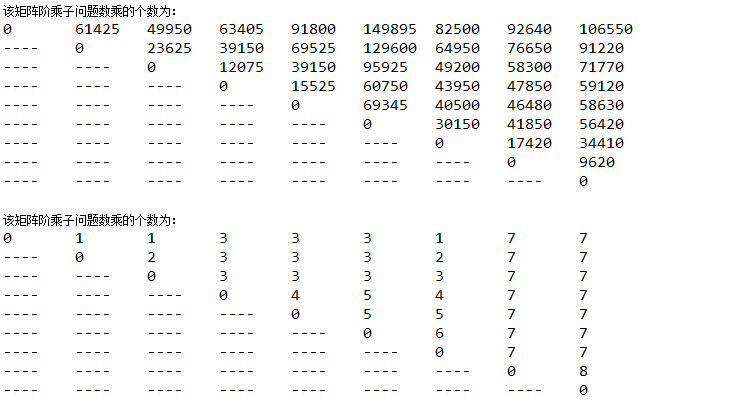

参考:http://blog.csdn.net/liufeng_king/article/details/8497607



