深度学习-神经网络 BP 算法推导过程

BP 算法推导过程

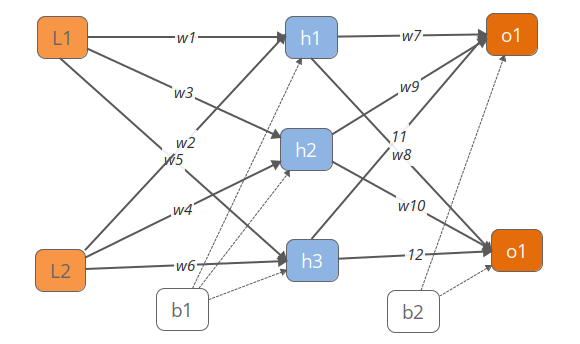
一.FP过程(前向-计算预测值)

定义sigmoid激活函数

import numpy as np
def sigmoid(z):
    return 1.0 / (1 + np.exp(-z))

输入层值和 标签结果

l = [5.0, 10.0]
y = [0.01,0.99]
alpha=0.5

初始化 w,b 的值

w = [0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65]
b = [0.35, 0.65]

计算隐层的结果

\[ h1 = Sigmod( Net_{h1}) =Sigmod(w1*l1+ w2*l2+b1*1) \]

h1 = sigmoid(w[0] * l[0] + w[1] * l[1] + b[0])
h2 = sigmoid(w[2] * l[0] + w[3] * l[1] + b[0])
h3 = sigmoid(w[4] * l[0] + w[5] * l[1] + b[0])
[h1,h2,h3]
#[0.9129342275597286, 0.9791636554813196, 0.9952742873976046]

[0.9129342275597286, 0.9791636554813196, 0.9952742873976046]

计算输出层的结果

\[ o1 = Sigmod( Net_{o1}) =Sigmod(w7*h1+ w9*h2+w11*h3+b2*1) \]

o1 = sigmoid(w[6] * h1 + w[8] * h2+ w[10] * h3 + b[1])
o2 = sigmoid(w[7] * h1 + w[9] * h2+ w[11] * h3 + b[1])
[o1,o2]
#[0.8910896614765176, 0.9043299248500164]

[0.8910896614765176, 0.9043299248500164]

计算整体loss误差值 (平方损失函数)

\[loss=E_{total}=E_{o1}+E_{o2}=\frac{1}{2}*(y_1-o1)^2+\frac{1}{2}*(y_2-o2)^2 \]

E_total=1/2*(y[0]-o1)**2+1/2*(y[1]-o2)**2
E_total
#0.3918291766685041

0.3918291766685041

二.BP过程 (反向-更新参数值)

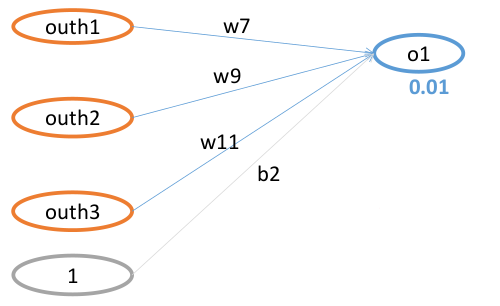
更新w7的值:

w7的值只和o1的损失函数有关系,所以整体Loss对w7求偏导,E_o2 会约掉
target 代表目标值

\[Loss=E_{total}=E_{o1}+E_{o2} \]

\[E_{o1}=\frac{1}{2}*(target_{o1}-out_{o1})^2 =\frac{1}{2}*(target_{o1}-Sigmod(net_{o1}))^2 \]

\[E_{o1} =\frac{1}{2}*(target_{o1}-Sigmod(w7*h1+ w9*h2+w11*h3+b2*1))^2 \]

同过复合函数链式求导发展的如下公式

\[\text{整体损失 对w7 求偏导 : } \frac{\partial E_{total}}{\partial w7} =\frac{\partial E_{total}}{\partial out_{o1}} *\frac{\partial out_{o1}}{\partial net_{o1}} *\frac{\partial net_{o1}}{\partial w7} \]

第一步: E_total 对 Out_o1 求导

\[\text{原函数 : } E_{total} =\frac{1}{2}(target_{o1}-out_{o1})^2+E_{o2} \]

\[\frac{\partial E_{total}}{\partial out_{o1}}=2*\frac{1}{2}*(target_{o1}-out_{o1})^{2-1}*-1+0 \]

(y[0]-o1)*(-1) #0.8910896614765176

0.8810896614765176

第二步: Out_o1 对 net_o1 求导
详见sigmod 函数求导公式

\[\text{原函数 } out_{o1}=\frac{1}{1+e^{-net_{o1}}} \]

\[\frac{\partial out_{o1}}{\partial net_{o1}}=out_{o1}(1-out_o) \]

o1*(1-o1) #0.09704887668618288

0.09704887668618288

第三步: Net_o1 对 w7 求导

\[\text{原函数 : } net_{o1} =w7*out_{h1}+ w9*out_{h2}+w11*out_{h3}+b2*1 \]

\[\frac{\partial net_{o1}}{\partial w7}=1*out_{h1}*w7^{(1-1)}+0+0+0 \]

1*h1*1 #0.9129342275597286

0.9129342275597286

组合整个求导过程

\[\text{整体损失 对w7 求偏导 : } \frac{\partial E_{total}}{\partial w7} =-1*(target_{o1}-out_{o1})*out_{o1}*(1-out_{o1})*out_{h1} \]

(o1-y[0])*o1*(1-o1)*h1 #0.07806387550033887

0.07806387550033887

第四部分 更新前向分布算法 更新w7的值
η指 学习率

\[w7^+=w7+Δw7=w7-η*\frac{\partial E_{total}}{\partial w7} \]

# w[6] = w[6]-alpha*(o1-y[0])*o1*(1-o1)*h1 # w7
# w[7] = w[7]-alpha*(o2-y[1])*o2*(1-o2)*h1 #w8
# w[8] = w[8]-alpha*(o1-y[0])*o1*(1-o1)*h2 #w9
# w[9] = w[9]-alpha*(o2-y[1])*o2*(1-o2)*h2 #w10
# w[10]=w[10]-alpha*(o1-y[0])*o1*(1-o1)*h3 #w11
# w[11]=w[11]-alpha*(o2-y[1])*o2*(1-o2)*h3 #w12

得到w7-w12的更新公式(后面一起更新)

# #提取公共部分
#t1=(o1-y[0])*o1*(1-o1)
#t2=(o2-y[1])*o2*(1-o2)

# w[6] = w[6]-alpha*t1*h1 #w7
# w[7] = w[7]-alpha*t2*h1 #w8
# w[8] = w[8]-alpha*t1*h2 #w9
# w[9] = w[9]-alpha*t2*h2 #w10
# w[10]=w[10]-alpha*t1*h3 #w11
# w[11]=w[11]-alpha*t2*h3 #w12
# print("新的w7的值:",w[6])
# w[6:]

更新w1的值:

\[\text{整体损失 对w1 求偏导 : } \frac{\partial E_{total}}{\partial w1} =\frac{\partial E_{total}}{\partial out_{h1}} *\frac{\partial out_{h1}}{\partial net_{h1}} *\frac{\partial net_{h1}}{\partial w1} \]

\[\text{展开 : } \frac{\partial E_{total}}{\partial w1}= (\frac{\partial E_{o1}}{\partial out_{h1}}+\frac{\partial E_{o2}}{\partial out_{h1}}) *\frac{\partial out_{h1}}{\partial net_{h1}} *\frac{\partial net_{h1}}{\partial w1} \]

第一步: E_o1对 out_h1 求偏导 and E_o2对 out_h1

\[\frac{\partial E_{o1}}{\partial out_{h1}}= \frac{\partial E_{o1}}{\partial out_{o1}} *\frac{\partial out_{o1}}{\partial net_{o1}} *\frac{\partial net_{o1}}{\partial out_{h1}} \]

\[\frac{\partial E_{o1}}{\partial out_{h1}}= -(target_{o1}-out_{o1}) *out_{o1}(1-out_{o1}) *w7 \]

-(y[0]-o1)*o1*(1-o1)*w[6] # E_o1 对out_h1  0.03420350476244207

0.03420350476244207

-(y[1]-o2)*o2*(1-o2)*w[7] # E_o1 对out_h1 -0.003335375074384934

-0.003335375074384934

第二步 out_h1 对net_h1 求偏导(前面计算过)

h1*(1-h1)

0.07948532370965024

第三步 net_h1 对w1 求篇导

\[\text{原函数 : } net_{h1} =w1*l1+ w2*l2+b1*1 \]

l[0]

5.0

最终整合 w1 的更新公式得

\[\frac{\partial E_{total}}{\partial w1}=[ -(target_{o1}-out_{o1})*out_{o1}(1-out_o1)*w7 -(target_{o2}-out_{o2})*out_{o2}(1-out_o2)*w8] *out_{o1}*(1-out_{o1}) *l1 \]

#w[0] = w[0]-alpha* w(-1*(y[0]-o1)*o1*(1-o1)*w[6]+-1*(y[1]-o2)*o2*(1-o2)*w[7])*h1*(1-h1)*l[0] # w1的更新值
# 提取公共部分



t1=(o1-y[0])*o1*(1-o1)
t2=(o2-y[1])*o2*(1-o2)

w[0] = w[0] - alpha * (t1 * w[6] + t2 * w[7]) * h1 * (1 - h1) * l[0]
w[1] = w[1] - alpha * (t1 * w[6] + t2 * w[7]) * h1 * (1 - h1) * l[1]
w[2] = w[2] - alpha * (t1 * w[8] + t2 * w[9]) * h2 * (1 - h2) * l[0]
w[3] = w[3] - alpha * (t1 * w[8] + t2 * w[9]) * h2 * (1 - h2) * l[1]
w[4] = w[4] - alpha * (t1 * w[10]+ t2 *w[11]) * h3 * (1 - h3) * l[0]
w[5] = w[5] - alpha * (t1 * w[10]+ t2 *w[11]) * h3 * (1 - h3) * l[1]

w[6] = w[6]-alpha*t1*h1 
w[7] = w[7]-alpha*t2*h1 
w[8] = w[8]-alpha*t1*h2 
w[9] = w[9]-alpha*t2*h2 
w[10]=w[10]-alpha*t1*h3 
w[11]=w[11]-alpha*t2*h3
print("进行一次跌倒更新后的结果")
print(w)

进行一次跌倒更新后的结果
[0.0938660917985833, 0.13773218359716657, 0.19802721973428622, 0.24605443946857242, 0.2994533791079845, 0.3489067582159689, 0.3609680622498306, 0.4533833089635062, 0.4581364640581681, 0.5536287533891512, 0.5574476639638248, 0.653688458944847]

输入值为 0.01,0.99 的第一次迭代对照结果

0.0938660917985833, 0.13773218359716657, 0.19802721973428622, 0.24605443946857242, 0.2994533791079845, 0.3489067582159689, 0.3609680622498306, 0.4533833089635062, 0.4581364640581681, 0.5536287533891512, 0.5574476639638248, 0.653688458944847

输入值为 0.00,1.00 的第一次迭代对照结果

0.09386631682087375, 0.13773263364174748, 0.1980267403252208, 0.24605348065044158, 0.2994531447534454, 0.34890628950689084, 0.3605250660434654, 0.4537782320399227, 0.4576613303938861, 0.5540523264259203, 0.556964712705892, 0.6541190012244457