霍夫线变换，霍夫圆变换

在图像处理和计算机视觉领域中，如何从当前的图像中提取所需要的特征信息是图像识别的关键所在。在许多应用场合中需要快速准确地检测出直线或者圆。其中一种非常有效的解决问题的方法是霍夫（Hough）变换，其为图像处理中从图像中识别几何形状的基本方法之一，应用很广泛，也有很多改进算法。最基本的霍夫变换是从黑白图像中检测直线(线段)。

1、霍夫变换

⑴霍夫变换概述

霍夫变换(Hough Transform)是图像处理中的一种特征提取技术，该过程在一个参数空间中通过计算累计结果的局部最大值得到一个符合该特定形状的集合作为霍夫变换结果。

霍夫变换于1962年由PaulHough首次提出，最初的Hough变换是设计用来检测直线和曲线，起初的方法要求知道物体边界线的解析方程，但不需要有关区域位置的先验知识。这种方法的一个突出优点是分割结果的Robustness,即对数据的不完全或噪声不是非常敏感。然而，要获得描述边界的解析表达常常是不可能的。后于1972年由Richard Duda & Peter Hart推广使用，经典霍夫变换用来检测图像中的直线，后来霍夫变换扩展到任意形状物体的识别，多为圆和椭圆。霍夫变换运用两个坐标空间之间的变换将在一个空间中具有相同形状的曲线或直线映射到另一个坐标空间的一个点上形成峰值，从而把检测任意形状的问题转化为统计峰值问题。

⑵霍夫线变换

我们知道，霍夫线变换是一种用来寻找直线的方法. 在使用霍夫线变换之前, 首先要对图像进行边缘检测的处理，也即霍夫线变换的直接输入只能是边缘二值图像.

OpenCV支持三种不同的霍夫线变换，它们分别是：

　　●标准霍夫变换(Standard Hough Transform，SHT)

　　●多尺度霍夫变换（Multi-Scale Hough Transform，MSHT）

　　●累计概率霍夫变换(Progressive Probabilistic Hough Transform ，PPHT)。

其中，多尺度霍夫变换（MSHT）为经典霍夫变换（SHT）在多尺度下的一个变种。累计概率霍夫变换(PPHT）算法是标准霍夫变换（SHT）算法的一个改进，它在一定的范围内进行霍夫变换，计算单独线段的方向以及范围，从而减少计算量，缩短计算时间。之所以称PPHT为“概率”的，是因为并不将累加器平面内的所有可能的点累加，而只是累加其中的一部分，该想法是如果峰值如果足够高，只用一小部分时间去寻找它就够了。这样猜想的话，可以实质性地减少计算时间。

在OpenCV中，我们可以用HoughLines函数来调用标准霍夫变换SHT和多尺度霍夫变换MSHT。

而HoughLinesP函数用于调用累计概率霍夫变换PPHT。累计概率霍夫变换执行效率很高，所有相比于HoughLines函数，我们更倾向于使用HoughLinesP函数。

总结一下，OpenCV中的霍夫线变换有如下三种：

　　<1>标准霍夫变换（StandardHough Transform，SHT），由HoughLines函数调用。

　　<2>多尺度霍夫变换（Multi-ScaleHough Transform，MSHT），由HoughLines函数调用。

　　<3>累计概率霍夫变换（ProgressiveProbabilistic Hough Transform，PPHT），由HoughLinesP函数调用。

⑶霍夫线变换的原理

【1】众所周知, 一条直线在图像二维空间可由两个变量表示. 如:

<1>在笛卡尔坐标系: 可由参数: 斜率和截距(m,b) 表示。

<2>在极坐标系: 可由参数: 极径和极角

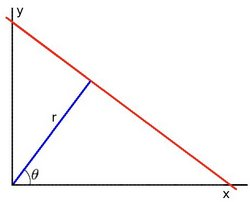
对于霍夫变换, 我们将采用第二种方式极坐标系来表示直线. 因此, 直线的表达式可为:

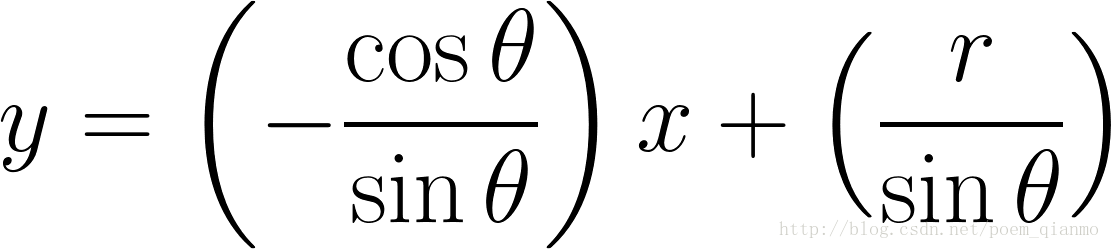
化简便可得到:

【2】一般来说对于点, 我们可以将通过这个点的一族直线统一定义为:

这就意味着每一对代表一条通过点的直线。

【3】如果对于一个给定点我们在极坐标对极径极角平面绘出所有通过它的直线, 将得到一条正弦曲线. 例如, 对于给定点X_0= 8 和Y_0= 6 我们可以绘出下图 (在平面):

这三条曲线在平面相交于点 (0.925, 9.6), 坐标表示的是参数对或者是说点, 点和点组成的平面内的的直线。

【5】以上的说明表明，一般来说, 一条直线能够通过在平面寻找交于一点的曲线数量来检测。而越多曲线交于一点也就意味着这个交点表示的直线由更多的点组成. 一般来说我们可以通过设置直线上点的阈值来定义多少条曲线交于一点我们才认为检测到了一条直线。

【6】这就是霍夫线变换要做的. 它追踪图像中每个点对应曲线间的交点. 如果交于一点的曲线的数量超过了阈值, 那么可以认为这个交点所代表的参数对在原图像中为一条直线。

2、霍夫圆变换

霍夫圆变换的基本原理和上面讲的霍夫线变化大体上是很类似的，只是点对应的二维极径极角空间被三维的圆心点x, y还有半径r空间取代。说“大体上类似”的原因是，如果完全用相同的方法的话，累加平面会被三维的累加容器所代替：在这三维中，一维是x，一维是y，另外一维是圆的半径r。这就意味着需要大量的内存而且执行效率会很低，速度会很慢。

对直线来说, 一条直线能由参数极径极角表示. 而对圆来说, 我们需要三个参数来表示一个圆, 也就是：