浅谈“踹”字典树

字典树，顾名思义它是棵树，是棵处理字符串的树，具体是棵什么样的树呢，我们可以举个栗子：

假设现在有四个字符串：ych，yk，devot：

那么这棵树大概长这个亚子：

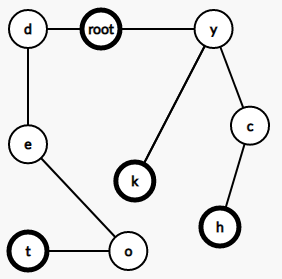
而图中加黑的点，也就是每个单词的终点；

主要用于查询前缀与单词？

然后咱们康实现：

1.插入一个单词：

首先我们设置了一个\(trie[i][j]\)数组(这里设trie树中全是小写英文字母,那这样对于每个节点，名义上是有26个子节点的。但是显然我们没必要将空间开的这么大，因为可能在一组数据中，有些字母是没有出现过的，所以我们用多少，开多少),表示以i为根的子树里，第j个字符的编号是多少。

可能有点抽象，我们以上图为例：

假设加入单词的顺序是：ych,yk,devot

那么(设1为根：

\[trie[1][24]=2;\to y\\ trie[2][2]=3;\ \ \to c\\ trie[3][7]=4;\ \ \to h\\ trie[2][10]=5;\to k\\ trie[1][3]=6;\ \ \to d\\ trie[6][4]=7; \ \ \to e\\ trie[7][14]=8;\to o\\ trie[8][19]=9;\to t \]

从这里可以看出，对于一个字母来说，它拥有两个编号，一个编号是固定不变的，也就是我们上面数组中的j，而另一个编号，同一个字母可以不同，取决于加入字典树的顺序，也就是\(trie[i][j]\)的值。

插入时，我们先判断是否有这个字母的节点，如果有，就直接在这个节点上继续操作，如果没有，新建一个节点，如此下去，一直插入到词尾

int tot=1;
void insert(char *s,int rt/*根*/) {
    for(int i=0;i<strlen(s);i++) {
        int x=s[i]-'a';
        if(trie[rt][x]==0) trie[rt][x]=++tot;//没有这个节点，新建
        rt=trie[rt][x];//递归下去
    }
    vis[rt]=1;//标记这是一个单词的最后
}

2.查询操作与插入操作异曲同工：

从根开始扫描某个字母是否出现过，顺着字典树往下找，如果中途发现没有某个节点，则证明没有；

如果找到最后，但vis[rt]=0，证明字典树中没有这个单词，但是有这个前缀；

bool search(char *s,int rt) {
  for(int i=0;i<strlen(s);i++) {
      int x=s[i]-'a';
      if(trie[rt][x]==0) return 0;
      rt=trie[rt][x];
  }
  if(vis[rt]) 
      return 1;
  return 0;
}

一道很简单的板子题：

Luogu P2580 于是他错误的点名开始了

（记得把数组开大

#include<bits/stdc++.h>

using namespace std;

int n,m;
char a[55];
int vis[1000000],talk[1000000];
int tot=1;
int trie[1000000][27];

void insert(char *s,int rt) {
	for(int i=0;i<strlen(s);i++) {
		int x=s[i]-'a';
		if(trie[rt][x]==0) 
			trie[rt][x]=++tot;
		rt=trie[rt][x];
	}
	vis[rt]=1;
}

int search(char *s,int rt) {
	for(int i=0;i<strlen(s);i++) {
		int x=s[i]-'a';
		if(trie[rt][x]==0) {return 0;}
		rt=trie[rt][x];
	}
	if(talk[rt]&&vis[rt]) 
		return 2;
	if(vis[rt]) {
		talk[rt]=1;
		return 1;
	}
	else {
		return 0;
	}
}

int main() {
	scanf("%d",&n);
	int rt=1;
	for(int i=1;i<=n;i++) {
		scanf("%s",a);
		insert(a,rt);
	}
	scanf("%d",&m);
	int bj;
	for(int i=1;i<=m;i++) {
		scanf("%s",a);
		bj=search(a,rt);
		if(bj==0) printf("WRONG\n");
		if(bj==1) printf("OK\n");
		if(bj==2) printf("REPEAT\n");
	}
	return 0;
}