双联通分量与二分图

我这是耽搁了多长时间才把它整完哈哈哈哈哈;
双联通分量
在无向图中,如果无论删去哪条边都不能使得 u 和 v 不联通,则称 u 和 v 边双连通;
在无向图中,如果无论删去哪个点(非 u 和 v)都不能使得 u 和v 不联通,则称 u 和 v 点双连通。
割点:删去该点,图分裂为多个连通块。
割边:也叫“桥”,删去该边,图分裂为多个连通块。
点双连通分量
类似地,定义$ d f n_u 和 low_u$。
如果 v 是 u 的子结点,并且 $low_v ≥ d f n_u $则点 u 是割点,删去点 u 后 v 子树和其它点不连通。
每个割点属于多个点双连通分量,**非割点只属于一个点双连通分量 **
缩完点是棵树或者森林;
边双连通分量
类似地,定义$ d f n_u 和 low_u$。
如果 v 是 u 的子结点,并且 \(low_v > d f n_u\) 则边 < u, v > 是割边。
每个点属于一个边双连通分量,边双连通分量之间以割边连接。
如何求:
//昨日tarjan
void tarjan(int u){
dfn[u]=low[u]=++cnt;
stk[++top]=u;
vis[u]=1;
for(int i=head[u];i;i=edge[i].nxt){
int v=edge[i].nxt;
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(vis[v]) low[u]=min(low[u],dfn[v]);
}
if(dfn[u]==low[u]){
++cnt;
do{
scc[stk[top]]=cnt;
vis[stk[top]]=0;
}while(stk[top--]!=u)
}
}
//求割点
void tarjan(int u,int f){
dfn[u]=low[u]=++cnt;
for(int i=head[i];i;i=edge[i].nxt){
int v=edge[i].to;
if(v!=f){
if(!dfn[v]) tarjan(v,u),
low[u]=min(low[u],low[v]);
else
low[u]=min(low[u],dfn[v]);
if(low[v]>=dfn[u]&&u!=root)
is_cut[u]=true;//u是割点
}
}
}
//求边双
void tarjan(int u,int f){
dfn[u]=low[u]=++cnt;
for(int i=head[i];i;i=edge[i].nxt){
int v=edge[i].to;
if(v!=f){
if(!dfn[v]) tarjan(v,u),
low[u]=min(low[u],low[v]);
else
low[u]=min(low[u],dfn[v]);
if(low[v]>dfn[u])
is_cut[u][v]=true;//<u,v>是割点
}
}
}
Luogu P3469
如果删去的不是割点,答案减少2(n-1);
割点:将割点删去,形成多个连通块了,然后答案就是:\(\sum\limits_{每一个连通块i}size[i]*\sum\limits_{j=连通块}^{j!=i}size[j]\)

先是缩点然后把每个边双变成一个点,找出所有叶子结点(度为1),之间相互连边,让最后没有任何一个点度为1
二分图
二分图:点黑白染色,邻点不同色。
如何判断一个给定的无向图是不是二分图?
从任意一点开始 BFS 或 DFS,起点不妨染色为白
当前在 u 点时,尝试将所有邻点染为不同的颜色
如果邻点已经染色且颜色不符,则不是二分图
二分图的等价条件 :
无向图是二分图当且仅当其不包含奇环。
二分图匹配
匹配:选取一些边,使得任意两条边没有公共点(每个点至多属于一条边)
最大匹配:选取边数尽可能多
完美匹配:所有点都在匹配中(每个点恰好属于一条边)
匹配边:选中的边
非匹配边:没有选中的边
匹配点:和选中边相连的点
非匹配点:和选中边不相连的点
常常将二分图的点画成两列
二分图最大匹配是一个常见问题。
匈牙利算法
网络流
匈牙利算法:
理论基础
交错路:从非匹配点出发,依次经过非匹配边、匹配边、非匹配边...
增广路:从非匹配点出发,结束于非匹配点的交错路
增广路定理:任意一个非最大匹配的匹配一定存在增广路
算法思想
初始没有选中的边
寻找增广路
找到增广路则将路径中匹配边和非匹配边对换
找不到增广路则当前为最大匹配
int girl[mxn],f[mxn][mxn];//girl[i]表示第i个点的匹配是哪个点,f[i][j]=0/1,表示第i个点和第j个点是否有一条连边;
bool vis[mxn]//vis[i]表示在此次匹配中第i个点有没有被考虑过,在下一轮中不一定,因此每次都要memset vis数组
memset(vis,0,sizeof(vis));
bool work(int u){
for(int i=0;i<n;i++){
if(!vis[i]&&f[i][u]){
vis[i]=1;
if(!girl[i]||find(girl[i])){
girl[i]=u;
return 1;
}
}
}
return 0;
}
记得这东西是我的假期计划(雾霾;
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int ans=0;
char last=' ',ch=getchar();
while(ch>'9'||ch<'0') last=ch,ch=getchar();
while(ch>='0'&&ch<='9') ans=(ans<<1)+(ans<<3)+ch-'0',ch=getchar();
if(last=='-') ans=-ans;
return ans;
}
const int mxn=1010;
const int mxm=1010;
int n,m,e;
int girl[mxm],f[mxn][mxm],vis[mxm];
bool work(int u){
for(int i=1;i<=m;i++){
if(!vis[i]&&f[u][i]){
vis[i]=1;
if(!girl[i]||work(girl[i])){
girl[i]=u;
return 1;
}
}
}
return 0;
}
int ans;
int main(){
n=read();m=read();e=read();
int u,v;
for(int i=1;i<=e;i++){
u=read();
v=read();
if(u>n||v>m) continue;
f[u][v]=1;
}
for(int i=1;i<=n;i++){
memset(vis,0,sizeof(vis));
ans+=work(i);
}
printf("%d",ans);
return 0;
}
看一个有情景的板子题:
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int ans=0;
char last=' ',ch=getchar();
while(ch>'9'||ch<'0') last=ch,ch=getchar();
while(ch>='0'&&ch<='9') ans=(ans<<1)+(ans<<3)+ch-'0',ch=getchar();
if(last=='-') ans=-ans;
return ans;
}
const int mxn=110;
const int mxm=210;
int n,m,e;
int girl[mxm],f[mxn][mxm],vis[mxm];
bool work(int u){
for(int i=m+1;i<=n;i++){
if(!vis[i]&&f[u][i]){
vis[i]=1;
if(!girl[i]||work(girl[i])){
girl[i]=u;
return 1;
}
}
}
return 0;
}
int ans;
int main(){
m=read();n=read();
int u,v;
for(int i=1;u!=-1&&v!=-1;i++){
u=read();
v=read();
f[u][v]=f[v][u]=1;
}
for(int i=1;i<=m;i++){
memset(vis,0,sizeof(vis));
ans+=work(i);
}
if(ans) printf("%d\n",ans);
else printf("No Solution!");
for(int i=m+1;i<=n;i++){
if(girl[i]){
printf("%d %d\n",girl[i],i);
}
}
return 0;
}
看一个有技术含量(建图方面)的模板
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int ans=0;
char last=' ',ch=getchar();
while(ch>'9'||ch<'0') last=ch,ch=getchar();
while(ch>='0'&&ch<='9') ans=(ans<<1)+(ans<<3)+ch-'0',ch=getchar();
if(last=='-') ans=-ans;
return ans;
}
const int mxn=105;
const int mxm=1000;
int n,m,head[mxn];
struct node{
int to,nxt;
}e[mxm];
int ecnt;
void add(int from,int to){
++ecnt;
e[ecnt].nxt=head[from];
e[ecnt].to=to;
head[from]=ecnt;
}
int girl[mxn];
bool vis[mxn];
int ans,tot;
bool is[mxn],home[mxn];
bool work(int u){
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(!vis[v]){
vis[v]=1;
if(!girl[v]||work(girl[v])){
girl[v]=u;
return 1;
}
}
}
return 0;
}
void clean(){
memset(is,0,sizeof(int)*(n+5));
memset(head,0,sizeof(int)*(n+5));
memset(girl,0,sizeof(int)*(n+5));
tot=0;ecnt=0;ans=0;
}
int main(){
int T,a;
T=read();
while(T--){
n=read();
clean();
for(int i=1;i<=n;i++)
is[i]=read();
for(int i=1;i<=n;i++){
home[i]=read();
if(is[i]&&home[i]==0) add(i,i);
if(!is[i]||(is[i]&&!home[i])) tot++;
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
a=read();
if(a&&is[j])
add(i,j);
}
}
for(int i=1;i<=n;i++){
if((is[i]&&!home[i])||!is[i]) {
memset(vis,0,sizeof(vis));
ans+=work(i);
}
}
if(ans==tot) printf("^_^\n");
else printf("T_T\n");
}
return 0;
}
网络流
取额外的两个点作为源点和汇点
源点向左边一列每个点连流量为 1 的边
右边一列每个点向汇点连流量为 1 的边
二分图中每条边从左向右连流量为 1 的边
求最大流即可
对于网络流大致是理解了,就是不断寻找曾广路,更新最终答案的过程。
除了写代码没有什么问题了
想要背板子:
EK算法:
#include<bits/stdc++.h>
#define inf 1000000007
using namespace std;
inline int read(){
int ans=0;
char last=' ',ch=getchar();
while(ch>'9'||ch<'0') last=ch,ch=getchar();
while(ch>='0'&&ch<='9') ans=(ans<<1)+(ans<<3)+ch-'0',ch=getchar();
if(last=='-') ans=-ans;
return ans;
}
bitset<10010> vis;
int n,m,s,t;
int ecnt=1,ans;
int head[10010];
struct node{
int to,dis,nxt;
}e[200010];
void add(int from,int to,int dis){
++ecnt;
e[ecnt].to=to;
e[ecnt].dis=dis;
e[ecnt].nxt=head[from];
head[from]=ecnt;
}
int now[10010],pre[10010];
bool bfs(){
vis.reset();
vis[s]=1;
queue<int> q;
q.push(s);
now[s]=inf;
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=head[u],v,w;i;i=e[i].nxt){
v=e[i].to;w=e[i].dis;
if(!w||vis[v]) continue;
now[v]=min(now[u],w);
pre[v]=i;
if(v==t) return 1;
q.push(v);
vis[v]=1;
}
}
return 0;
}
void update(){
ans+=now[t];
int x=t;
while(x!=s){
int i=pre[x];
e[i].dis-=now[t];
e[i^1].dis+=now[t];
x=e[i^1].to;
}
}
int main(){
n=read();m=read();
s=read();t=read();
int u,v,w;
for(int i=1;i<=m;i++){
u=read();
v=read();
w=read();
add(u,v,w);
add(v,u,0);
}
while(bfs())update();
printf("%d",ans);
}
然后一个基本和板子一样的题:Luogu P2740 [USACO4.2] 草地排水Drainage Ditches
网络流解决二分图匹配:
Dinic算法:
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int ans=0;
char last=' ',ch=getchar();
while(ch>'9'||ch<'0') last=ch,ch=getchar();
while(ch>='0'&&ch<='9') ans=(ans<<1)+(ans<<3)+ch-'0',ch=getchar();
if(last=='-') ans=-ans;
return ans;
}
const int mxn=10010;
const int mxm=100010;
const int inf=2147483647;
int n,m,s,t;
struct node{
int to,dis,nxt;
}e[mxm<<1];
int ecnt=1,head[mxn],dep[mxn],cur[mxn];
void add(int from,int to,int dis){
ecnt++;
e[ecnt].to=to;
e[ecnt].dis=dis;
e[ecnt].nxt=head[from];
head[from]=ecnt;
}
bool bfs(){
queue<int> q;
while(!q.empty()) q.pop();
memset(dep,0,sizeof(dep));
q.push(s);
dep[s]=1;
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=head[u],v;i;i=e[i].nxt){
v=e[i].to;
if(e[i].dis>0&&!dep[v]){
dep[v]=dep[u]+1;
q.push(v);
}
}
}
if(dep[t]==0) return 0;
return 1;
}
int dfs(int u,int dis){
if(u==t) return dis;
for(int &i=cur[u];i;i=e[i].nxt){
int v=e[i].to;
if(dep[v]==dep[u]+1&&e[i].dis!=0){
int k=dfs(v,min(dis,e[i].dis));
if(k>0){
e[i].dis-=k;
e[i^1].dis+=k;
return k;
}
}
}
return 0;
}
int main(){
n=read();m=read();
s=read();t=read();
int u,v,w;
for(int i=1;i<=m;i++){
u=read();v=read();w=read();
add(u,v,w);add(v,u,0);
}
int d,ans=0;
while(bfs()){
for(int i=1;i<=n;i++)cur[i]=head[i];
while(d=dfs(s,inf)) ans+=d;
}
printf("%d",ans);
return 0;
}
然后我学习网络流的初衷:如何用dinic算法来解决二分图匹配问题:
首先我们需要建立一个超级源点S,还要建立一个超级汇点T;
然后我们将所有在左边的点和源点S连一条长度为1的边,将所有在右边的点和汇点T连一条长度为1的边,对于中间的边,我们按照输入加入长度为1的边,然后跑一边由S到T的网络最大流就可以得到结果啦。
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int ans=0;
char last=' ',ch=getchar();
while(ch>'9'||ch<'0') last=ch,ch=getchar();
while(ch>='0'&&ch<='9') ans=(ans<<1)+(ans<<3)+ch-'0',ch=getchar();
if(last=='-') ans=-ans;
return ans;
}
const int mxn=10010;
const int mxm=1000010;
const int inf=2147483647;
int n,m,ee;
int s,t;
struct node{
int to,dis,nxt;
}e[mxm<<1];
int ecnt=1,head[mxn],dep[mxn],cur[mxn];
void add(int from,int to,int dis){
ecnt++;
e[ecnt].to=to;
e[ecnt].dis=dis;
e[ecnt].nxt=head[from];
head[from]=ecnt;
}
bool bfs(){
queue<int> q;
while(!q.empty()) q.pop();
memset(dep,0,sizeof(dep));
q.push(s);
dep[s]=1;
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=head[u],v;i;i=e[i].nxt){
v=e[i].to;
if(e[i].dis>0&&!dep[v]){
dep[v]=dep[u]+1;
q.push(v);
}
}
}
if(dep[t]==0) return 0;
return 1;
}
int dfs(int u,int dis){
if(u==t) return dis;
for(int &i=cur[u];i;i=e[i].nxt){
int v=e[i].to;
if(dep[v]==dep[u]+1&&e[i].dis!=0){
int k=dfs(v,min(dis,e[i].dis));
if(k>0){
e[i].dis-=k;
e[i^1].dis+=k;
return k;
}
}
}
return 0;
}
int main(){
n=read();m=read();
ee=read();
int u,v;
int nn=n+m+2;
for(int i=1;i<=n;i++){
add(1,i+1,1);
add(i+1,1,0);
}
for(int i=1;i<=ee;i++){
u=read();v=read();
if(u<=n&&v<=m){
add(u+1,v+n+1,1);
add(v+n+1,u+1,0);
}
}
for(int i=1;i<=m;i++){
add(i+n+1,nn,1);
add(nn,i+n+1,0);
}
s=1;t=nn;
int d,ans=0;
while(bfs()){
for(int i=1;i<=nn;i++)cur[i]=head[i];
while(d=dfs(s,inf)) ans+=d;
}
printf("%d",ans);
return 0;
}
一些很神奇的结论:
1.最小定点覆盖:
二分图的最小顶点覆盖=最大匹配数
2.最小路径覆盖:
DAG最小路径覆盖=图顶点-建图后的最大匹配
然后最小路径覆盖的两种建图套路:
1.求最小不相交路径覆盖:
建图方式:把一个的点V拆点成Vx和Vy,如果A连向B,那么就建一条Ax连向By的边。
图中有多少条路径,可以以一种方法得到,就是计算出度为0的点的个数。
2.最小相交路径覆盖:
做法首先跑floyd,求出原图的传递闭包,然后用上述方法做即可。?开始一脸懵逼rwr??
3.最小边覆盖
最小边覆盖=图顶点-最大匹配
POJ 3041 Asteroids
一个 N × N 的网格中,有 K 个大小为 1 × 1 的小行星,现在可以用激光枪每次消灭一行的小行星或者消灭一列的小行星。问最少需要使用多少次激光枪消灭所有的小行星。
将x放在左边y放在右边,如果有一个小行星在(x,y),那么由x向y连边,每行为左边一点,每列为右边一点,每个小行星为一边
选择最少的点覆盖所有边 =最大匹配数

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<queue>
using namespace std;
inline int read() {
int ans=0;
char last=' ',ch=getchar();
while(ch>'9'||ch<'0') last=ch,ch=getchar();
while(ch>='0'&&ch<='9') ans=(ans<<1)+(ans<<3)+ch-'0',ch=getchar();
if(last=='-') ans=-ans;
return ans;
}
const int mxm=100010;
const int mxn=10010;
const int inf=2147483647;
int n,m,s,t;
struct node{
int to,dis,nxt;
}e[mxm<<1];
int ecnt=1,head[mxn],cur[mxn],dep[mxn];
void add(int from,int to,int dis){
ecnt++;
e[ecnt].dis=dis;
e[ecnt].to=to;
e[ecnt].nxt=head[from];
head[from]=ecnt;
}
bool bfs(){
queue<int> q;
while(!q.empty()) q.pop();
q.push(s);
memset(dep,0,sizeof(dep));
dep[s]=1;
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(!dep[v]&&e[i].dis>0){
dep[v]=dep[u]+1;
q.push(v);
}
}
}
if(dep[t]==0) return 0;
return 1;
}
int dfs(int u,int l){
if(u==t) return l;
for(int &i=cur[u];i;i=e[i].nxt){
int v=e[i].to;
if(dep[v]==dep[u]+1&&e[i].dis!=0){
int id=dfs(v,min(e[i].dis,l));
if(id>0){
e[i].dis-=id;
e[i^1].dis+=id;
return id;
}
}
}
return 0;
}
int k,r,c;
int main() {
n=read();
k=read();
s=0;t=2*n+1;
for(int i=1;i<=n;i++){
add(s,i,1);
add(i,s,0);
}
for(int i=1;i<=k;i++){
r=read();c=read();
c+=n;
add(r,c,1);
add(c,r,0);
}
for(int i=1;i<=n;i++){
add(i+n,t,1);
add(t,i+n,0);
}
int d,ans=0;
while(bfs()){
for(int i=s;i<=t;i++) cur[i]=head[i];
while(d=dfs(s,inf)) ans+=d;
}
printf("%d",ans);
return 0;
}
最小路径覆盖
给定有向图 G =< V, E >。设 P 是 G 的一个简单路(顶点不相交)的集合。如果 V 中每个顶点恰好在 P 的一条路上,则称 P是 G 的一个路径覆盖。 P 中路径可以从 V 的任何一个顶点开始,长度也是任意的,特别地,可以为 0。 G 的最小路径覆盖是 G 的所含路径条数最少的路径覆盖
最小路径覆盖 = 点数 - 二分图最大匹配
二分图:将原图每个点拆分为入点和出点,如果原图存在 u 到 v的边,则在 u 的出点和 v 的入点间连无向边。
我居然听懂了ww?
最差的想法,每个点都给它安排一条边,共有n条路径。
对于每条边,先覆盖一个点,然后显然这条边还可以覆盖另一个点,那么我们就可以减少一条边。为了使方案最小,我们需要保证一个点只有一条边出去,只有一条边进入,在原图中路径覆盖,就是在二分图中匹配。这样每选中一条这样的边我们就可以在n条边中减去一条路径,就在n条边减去一条路径;
那么我们也就可以转化为二分图,求最大匹配数;
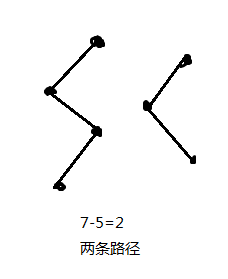


好了我乱了??
巧了怎么又讲了一遍ww?
非常难过的不知道re了多少遍以后终于艰难的ac啦!
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<queue>
using namespace std;
inline int read() {
int ans=0;
char last=' ',ch=getchar();
while(ch>'9'||ch<'0') last=ch,ch=getchar();
while(ch>='0'&&ch<='9') ans=(ans<<1)+(ans<<3)+ch-'0',ch=getchar();
if(last=='-') ans=-ans;
return ans;
}
const int mxm=200000;
const int mxn=500;
const int inf=2147483647;
int n,m,s,t;
bool pd[mxn];
struct node{
int to,dis,nxt;
}e[mxm<<1];
int ecnt=1,head[mxn],cur[mxn],dep[mxn];
void add(int from,int to,int dis){
ecnt++;
e[ecnt].dis=dis;
e[ecnt].to=to;
e[ecnt].nxt=head[from];
head[from]=ecnt;
}
bool bfs(){
queue<int> q;
while(!q.empty()) q.pop();
q.push(s);
memset(dep,0,sizeof(dep));
dep[s]=1;
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(!dep[v]&&e[i].dis>0){
dep[v]=dep[u]+1;
q.push(v);
}
}
}
if(dep[t]==0) return 0;
return 1;
}
int to[mxn],tag[mxn];
int dfs(int u,int l){
if(u==t) return l;
int rtn=0;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(rtn==l) return l;
if(dep[v]==dep[u]+1&&e[i].dis>0){
int id=dfs(v,min(e[i].dis,l-rtn));
rtn+=id;e[i].dis-=id;e[i^1].dis+=id;
if(id!=0&&u!=s&&v!=t&&v>n) {to[u]=v-n;tag[v-n]=u;}
}
}
if(rtn==0) dep[u]=0;
return rtn;
}
int k,r,c;
void op(int x){
if(x==0) return;
if(tag[x]!=x) op(tag[x]);
pd[x]=true;
printf("%d ",x);
}
int main() {
memset(pd,0,sizeof(pd));
n=read();
k=read();
s=0;t=2*n+1;
for(int i=1;i<=n;i++) to[i]=tag[i]=i;
for(int i=1;i<=n;i++){
add(s,i,1);
add(i,s,0);
}
for(int i=1;i<=k;i++){
r=read();c=read();
c+=n;
add(r,c,1);
add(c,r,0);
}
for(int i=1;i<=n;i++){
add(i+n,t,1);
add(t,i+n,0);
}
int d,ans=0;
while(bfs()){
d=dfs(s,inf);
while(d) ans+=d,d=dfs(s,inf);
}
for(int i=n;i>=1;i--){
if(to[i]==i&&pd[i]==false) {
op(i);
printf("\n");
}
}
printf("%d",n-ans);
return 0;
}
BZOJ 2150 部落战争
lanzerb 的部落在 A 国的上部,他们不满天寒地冻的环境,于是准备向 A 国的下部征战来获得更大的领土。 A 国是一个 M × N的矩阵,其中某些地方是城镇,某些地方是高山深涧无人居住。lanzerb 把自己的部落分成若干支军队,他们约定:
- 每支军队可以从任意一个城镇出发,并只能从上往向下征战,途中只能经过城镇,可以在任意一个城镇停止征战。
- 每个城镇只能被一支军队经过。
- 行军方式类似国际象棋中的马,不过只能走 R × C 的路线。
lanzerb 的野心使得他的目标是统一全国,但是兵力的限制使得他们在配备人手时力不从心。假设他们每支军队都能顺利占领这支军队经过的所有城镇,请你帮 lanzerb 算算至少要多少支军队才能完成统一全国的大业。
然后因为点数开小了,所以re了一天rwr 难过了;
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int ans=0;
char last=' ',ch=getchar();
while(ch>'9'||ch<'0') last=ch,ch=getchar();
while(ch>='0'&&ch<='9') ans=(ans<<1)+(ans<<3)+ch-'0',ch=getchar();
if(last=='-') ans=-ans;
return ans;
}
const int mx=60;
const int mxn=6000;
const int mxm=10000000;
const int inf=2147483647;
int m,n,r,c;
bool mp[mx][mx],vis[mxn];
int NUM[mx][mx];
int da[2]={1,1};
int db[2]={1,-1};
int dx[4],dy[4];
int head[mxn],ecnt=1;
int s,t,nn;
struct node{
int to,dis,nxt;
}e[mxm];
void add(int from,int to,int dis){
// cout<<from<<" "<<to<<endl;
ecnt++;
e[ecnt].dis=dis;
e[ecnt].nxt=head[from];
e[ecnt].to=to;
head[from]=ecnt;
}
bool Getread(){
char ch;
do{
ch=getchar();
}while(ch=='\r'||ch=='\n'||ch=='\0'||ch==' '||ch=='\t');
return ch=='.'?1:0;
}
bool pan(int x,int y){
return x>=1&&y>=1&&x<=m&&y<=n&&mp[x][y]==1;
}
int dep[mxn];
bool bfs(){
queue<int> q;
while(!q.empty()) q.pop();
q.push(s);
memset(dep,0,sizeof(dep));
dep[s]=1;
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(!dep[v]&&e[i].dis>0){
dep[v]=dep[u]+1;
q.push(v);
}
}
}
if(dep[t]==0) return 0;
return 1;
}
int dfs(int u,int l){
if(u==t) return l;
int rtn=0;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(rtn==l) return l;
if(dep[v]==dep[u]+1&&e[i].dis>0){
int id=dfs(v,min(e[i].dis,l));
rtn+=id;e[i].dis-=id;e[i^1].dis+=id;l-=id;
}
if(!l) break;
}
if(rtn==0) dep[u]=-1;
return rtn;
}
int SUM;
void Add(int x,int y){
int node=NUM[x][y];
for(int i=0;i<4;i++){
int xx=x+dx[i],yy=y+dy[i];
if(pan(xx,yy)) {
int nod=NUM[xx][yy]+SUM;
add(node,nod,1);
add(nod,node,0);
}
}
}
int main(){
m=read();n=read();
r=read();c=read();
dx[0]=r;dx[1]=r;dx[2]=c;dx[3]=c;
dy[0]=c;dy[1]=-c;dy[2]=r;dy[3]=-r;
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++){
mp[i][j]=Getread();
if(mp[i][j]) {
SUM++;
NUM[i][j]=SUM;
}
}
s=0;t=2*SUM+1;
for(int i=1;i<=SUM;i++){
add(s,i,1);
add(i,s,0);
}
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
if(mp[i][j]) Add(i,j);
for(int i=1;i<=SUM;i++){
add(i+SUM,t,1);
add(t,SUM+i,0);
}
int d,ans=0;
while(bfs()){
d=dfs(s,inf);
while(d) ans+=d,d=dfs(s,inf);
}
printf("%d",SUM-ans);
return 0;
}
差分约束
差分约束可以确定特定的不等式组是否存在解。
为每个变量 \(x_i\) 建立一个点 \(p_i\)。
如果要求 \(x_i - x_ j ≤ a\),则建立一条从 \(p _j\) 到 \(p_i\) 长度为 a 的边
以任意一点为起点求单源最短路,则一定有 \(d_i - d_j ≤ a\)
如果关系是\(d_i-d_j>a\),那么我们转化为\(d_i-d_j>=a+1\)
如果关系是\(d_i-d_j=a\),那就从\(p_i\)向\(p_j\)连边,\(p_j\)向\(p_i\)连边
如果出现负环,则归结出形如 \(x_i - x_i < 0\) 的约束,不等式组无解。
如果没有负环,最短路算法得到的距离数组就是一组合法的解。
相当于将这些数之间的大小关系串起来了;
BZOJ 2330&Luogu 3275 糖果
幼儿园里有 N 个小朋友, lxhgww 老师现在想要给这些小朋友们分配糖果,要求每个小朋友都要分到糖果。但是小朋友们也有嫉妒心,总是会提出一些要求,比如小明不希望小红分到的糖果比他的多,于是在分配糖果的时候, lxhgww 需要满足小朋友们的K 个要求。幼儿园的糖果总是有限的, lxhgww 想知道他至少需要准备多少个糖果,才能使得每个小朋友都能够分到糖果,并且满足小朋友们所有的要求。
N ≤ 100000, K ≤ 100000
每个限制为三个整数: X, A, B。
-
如果 X=1,表示第 A 个小朋友分到的糖果必须和第 B 个小朋友分到的糖果一样多;
-
如果 X=2,表示第 A 个小朋友分到的糖果必须少于第 B 个小朋友分到的糖果;
-
如果 X=3,表示第 A 个小朋友分到的糖果必须不少于第 B个小朋友分到的糖果;
-
如果 X=4,表示第 A 个小朋友分到的糖果必须多于第 B 个小朋友分到的糖果;
-
如果 X=5,表示第 A 个小朋友分到的糖果必须不多于第 B个小朋友分到的糖果;
建图:
对于x=1的情况,由A向B建一条长度为0的边,并且由B向A建一条长度为0的边。
对于x=2的情况,由A向B建一条长度为1的边,表示B比A至少多一个糖果。
对于x=3的情况,由B向A建一条长度为0的边,(由糖果数少的指向多的)。
对于x=4的情况,由B向A建一条长度为1的边,表示A比B至少多一个糖果。
对于x=5的情况,由A向B建一条长度为0的边,(由糖果数少的指向多的)。
建一个超级原点0(用超级原点来限制 糖果数>=1),从超级原点向每个点连一条长度为1的边。
从超级原点出发跑==最长路,判断是否有环=>无解
判断连边顺序:考虑最长路dis[v]>=dis[u]+w;
易见每种限制都可以表示为差分约束形式的不等式。
然后这道题跑单源最长路也是很迷惑对吧√
画个图理解(李姐)一下(盗的)
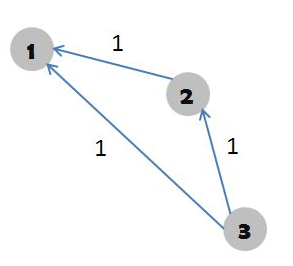
你看介个图,如果跑最短路,1号点的dis=1,但显而易见,1号点的答案应该是2才是合法的,因此我们需要跑最长路,才能满足所有的约束条件。
对于情况2和情况4,如果出现了a>a或者a<a的情况,显然是无解的。
然后spfa判环,如果有一个点进入队列n-1次,就有环了?然后无解输出。
最后,记录答案的变量要记得开 long long
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int ans=0;
char last=' ',ch=getchar();
while(ch>'9'||ch<'0') last=ch,ch=getchar();
while(ch>='0'&&ch<='9') ans=(ans<<1)+(ans<<3)+ch-'0',ch=getchar();
if(last=='-') ans=-ans;
return ans;
}
const int mxm=300010;
const int mxn=300010;
int n,k;
int head[mxn],ecnt;
struct node{
int to,dis,nxt;
}e[mxm<<1];
void add(int from,int to,int dis){
++ecnt;
e[ecnt].to=to;
e[ecnt].dis=dis;
e[ecnt].nxt=head[from];
head[from]=ecnt;
}
queue<int> q;
bool bj,vis[mxn];
long long dis[mxn],cnt[mxn];
void spfa(int s){
q.push(s);
vis[s]=1;
while(!q.empty()){
int u=q.front();
q.pop();
vis[u]=0;
if(cnt[u]==n-1){
bj=1;
return;
}
cnt[u]++;
for(int i=head[u],v,w;i;i=e[i].nxt){
v=e[i].to;w=e[i].dis;
if(dis[v]<dis[u]+w){
dis[v]=dis[u]+w;
if(!vis[v]) {
q.push(v);
vis[v]=1;
}
}
}
}
}
long long ans;
int main(){
int x,a,b;
n=read();k=read();
for(int i=1;i<=k;i++){
x=read();a=read();b=read();
if(x==1) {
add(a,b,0);
add(b,a,0);
}
if(x==2) {
if(a==b) {
printf("-1");
return 0;
}
add(a,b,1);
}
if(x==3)
add(b,a,0);
if(x==4) {
if(a==b) {
printf("-1");
return 0;
}
add(b,a,1);
}
if(x==5)
add(a,b,0);
}
for(int i=n;i>=1;i--) add(0,i,1);
spfa(0);
if(bj){
printf("-1");
return 0;
}
for(int i=1;i<=n;i++) {
if(dis[i]==0) {
printf("-1");
return 0;
}
ans+=dis[i];
}
printf("%lld",ans);
return 0;
}
BZOJ 1202 狡猾的商人
***姹接到一个任务,为税务部门调查一位商人的账本,看看账本是不是伪造的。账本上记录了 n 个月以来的收入情况,其中第 i个月的收入额为 Ai(i=1,2,3...n-1,n),。当 Ai 大于 0 时表示这个月盈利 Ai 元,当 Ai 小于 0 时表示这个月亏损 Ai 元。所谓一段时间内的总收入,就是这段时间内每个月的收入额的总和。***姹的任务是秘密进行的,为了调查商人的账本,她只好跑到商人那里打工。她趁商人不在时去偷看账本,可是她无法将账本偷出来,每次偷看账本时她都只能看某段时间内账本上记录的收入情况,并且她只能记住这段时间内的总收入。现在,***姹总共偷看了 m 次账本,当然也就记住了 m 段时间内的总收入,你的任务是根据记住的这些信息来判断账本是不是假的。
以 \(S_i\) 表示 \(A_i\) 的前缀和,则每个限制形如 \(S_u - S_v = k\),将其拆分为两个不等式
- \(S_u - S_v ≤ k\)
- \(S_u - S_v ≥ k 即 S_v - S_u ≤ -k\)
差分约束后如果出现负环,则信息有假。
当然,对于这种全部为等式的差分约束问题,用 DFS 或 BFS 判断即可,不需要应用最短路算法。
我数组又开小了(难过了
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int ans=0;
char last=' ',ch=getchar();
while(ch>'9'||ch<'0') last=ch,ch=getchar();
while(ch>='0'&&ch<='9') ans=(ans<<1)+(ans<<3)+ch-'0',ch=getchar();
if(last=='-') ans=-ans;
return ans;
}
const int inf=0x3f3f3f3f;
const int N=5005;
const int M=1000005;
int n,m;
struct node{
int to,dis,nxt;
}e[M];
int head[N],ecnt;
void add(int from,int to,int dis){
++ecnt;
e[ecnt].dis=dis;
e[ecnt].nxt=head[from];
e[ecnt].to=to;
head[from]=ecnt;
}
int dis[N],vis[N],in[N];
queue<int> q;
bool spfa(int s){
for(int i=0;i<=n;i++) dis[i]=-inf,vis[i]=0;
while(!q.empty()) q.pop();
q.push(s);
vis[s]=1;
dis[s]=0;
while(!q.empty()){
int u=q.front();
q.pop();
vis[u]=0;
in[u]++;
if(in[u]==n) return 0;
for(int i=head[u],v,w;i;i=e[i].nxt){
v=e[i].to;w=e[i].dis;
if(dis[v]<dis[u]+w) {
dis[v]=dis[u]+w;
if(!vis[v]) {
q.push(v);
vis[v]=1;
}
}
}
}
return 1;
}
int main(){
int t;
bool bj;
t=read();
while(t--){
for(int i=0;i<=n;i++) head[i]=in[i]=0;
n=read();m=read();
for(int i=1,u,v,w;i<=m;i++){
u=read();v=read();w=read();
add(u-1,v,w);
add(v,u-1,-w);
}
bj=1;
for(int i=0;i<=n;i++)
if(!in[i]) {
bj=spfa(i);
if(!bj) break;
}
if(!bj) printf("false\n");
else printf("true\n");
}
return 0;
}
BZOJ 4500 矩阵
有一个 n × m 的矩阵,初始每个格子的权值都为 0,可以对矩阵
执行两种操作:
- 选择一行,该行每个格子的权值加 1 或减 1。
- 选择一列,该列每个格子的权值加 1 或减 1。
现在有 K 个限制,每个限制为一个三元组 (x,y,c),代表格子(x,y) 权值等于 c。问是否存在一个操作序列,使得操作完后的矩阵满足所有的限制。如果存在输出”Yes”,否则输出”No”。
左边n个点代表行,右边m个点代表列;+
a,luogu没有的题,gu掉吧;




