概率与期望dp相关
概率与期望dp
概率
某个事件A发生的可能性的大小,称之为事件A的概率,记作P(A)。
假设某事的所有可能结果有n种,每种结果都是等概率,事件A涵盖其中的m种,那么P(A)=m/n。
例如投掷一枚骰子,点数小于3的概率为2/6=1/3。
如果两个事件A和B所涵盖的结果没有交集,那么P(A或B发生)=P(A)+P(B)
还是掷骰子
P(点数小于3或点数大于4)=2/6+2/6=2/3
如果A和B所涵盖的结果有交集
那么P(A或B发生)=P(A)+P(B)-P(A与B同时发生)
P(点数小于3或点数为偶数)=2/6+3/6-1/6=2/3
记事件B为“事件A不发生”
那么P(A)+P(B)=1,即P(B)=1-P(A)
P(点数不小于3)=1-2/6=2/3
在两个互不干扰的事中,事件A在其中一件事中,事件B在另外一件事中
那么P(A与B同时发生)=P(A)*P(B)
掷两个骰子, P(第一个点数小于3且第二个点数为偶数)=(2/6)×(3/6)=1/6
期望
事件A有多种结果,记其结果的大小为x,那么x的期望值表示事件A的结果的平均大小,记作E(x)。
E(x)=每种结果的大小与其概率的乘积的和。
例如,记掷一枚骰子的点数为x
E(x)=1*(1/6)+2*(1/6)+3*(1/6)+4*(1/6)+5*(1/6)+6*(1/6)=7/2
若c为常数,那么:
E(x+c)=E(x)+c, E(c*x)=c*E(x)
E(x+c)=(1+c)*(1/6)*……*(6+c)*(1/6);
记两个事件的结果分别为x,y
E(x+y)=E(x)+E(y)
例如: E(语文成绩+数学成绩)=E(语文成绩)+E(数学成绩)
可以举一个例子证明是正确的;
若两个事件互相独立, E(x*y)=E(x)*E(y)
E(语文成绩*数学成绩)=E(语文成绩)*E(数学成绩)
概率与期望的计算有一个共同的计算技巧:
若事件所产生的所有方案都是等概率的,那么一些概率与期望即可转化为一个计数问题,算出后再除以总方案数即可。
如求事件符合条件A的概率,则转化为对符合A的方案数的计数问题;若求方案的价值的期望值,则转化为所有方案的价值总和的计数问题。
解释:E(x)=case1*p1+case*p2+case3*p3……+casen*pn,因为是等概率问题,p1=p2=……=pn,因此我们可以把所有case值加起来然后再*p;
概率和期望的计算
概率与期望的计算也经常用的其加法和乘法规则。
尤其是期望的加法规则,在期望的计算中十分常用。 如求最大值与最小值之差的期望,则分别求二者的期望值再作差即可。
乘法规则时,要注意事件是否互相独立
概率与期望还可以通过列方程的方法计算。
有4张卡片,写着0,1,2,3,每次抽出一张并放回,反复抽,抽出0为止。问抽取的次数的期望值。
设抽取次数为x,则:
x=1+x*3/4
x=4
1表示第一次一定需要抽一次,然后对于一个状态,有1/4概率抽到0,那么继续抽取的次数是0,因此为1/4*0,有3/4的概率抽到其余的,需要继续抽,此时期望还是x个,所以就是3/4*x
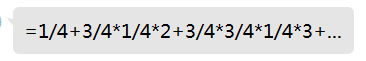
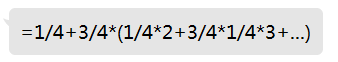
就差不多↑的感觉
BZOJ1867 钉子和小球

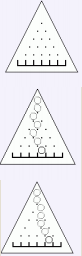
n<=50;
比较简单的概率dp
如果某一个的钉子(x,y)不见了,那么小球垂直下落,就转移到了(x+2,j+1);
设\(f[i][j]\)为小球经过第i行第j列的概率。
$f[1][1]=1 \((即起状态概率为1
\)f[i][j]=f[i-1][j-1] * [(i-1,j-1)有钉子]1/2
+f[i-1][j] * [(i-1,j)有钉子]1/2
+f[i-2][j-1] * [(i-2,j-1)没有钉子]$
\([(i-1,j-1)有钉子]\)可以看做一个bool的0/1数组,有钉子为1,没钉子为0;
至于分数输出,自定义分数数据类型并用gcd化简分数即可。
Bzoj5004 开锁魔法II
有 n 个箱子,每个箱子里有且仅有一把钥匙,每个箱子有且仅有一把钥匙可以将其打开。现在随机打开 m 个箱子,求能够将所有箱子打开的概率。
100组数据, k<=n<=300。
总方案数Cnm
题目约定了每个点的入度和出度均为1,因此最终的图一定是若干个环。每个环都至少选择一个点即可满足要求。求概率,实际上就是求方案数,最后再除以总方案数即可。
预处理出每个环的点数 c[i] 以及其后缀和 sum[i] 。
设$ f[i][j] \(表示前 i 个环中选出 j 个点,满足最终条件每个环都选的方案数。初始化\) f[0][0]=1$ 。
枚举 i 和 前 i 个环选的点数 j 、第 i 个环选的点数 k
可得\(f[i][j]=\sum\limits_{k=1}^{c[i]}f[i-1][j-k]*C^k_{c[i]}\)
BZOJ5091 摘苹果
在花园中有n棵苹果树以及m条双向道路,每条道路的两端连接着两棵不同的苹果树。假设第i棵苹果树连接着di条道路。小Q将会按照以下方式去
采摘苹果:
1.随机移动到一棵苹果树下,移动到第i棵苹果树下的概率为di/2m,但不在此采摘。
2.重复以下操作k次:等概率随机选择一条与当前苹果树相连的一条道路,移动到另一棵苹果树下,假设当前位于第i棵苹果树下,则他会采摘ai个苹果,多次经过同一棵苹果树下会重复采摘。
请计算小Q期望摘到多少苹果。 n,k<=100000,m<=200000
首先证明这是等概率事件:
设\(f[i][j]\)表示进行了i次操作走到j的概率,易知\(f[0][j]=\frac{dj}{2m}\)(从哪个点开始摘1)
然后考虑转移:第一步从起点走与起点相连的每一条边的概率都是\(\frac{1}{d_j}\)
然后对于整个图来说,第一步走每条边的概率就是第0步(1操作)选择这个点的概率*\(\frac{1}{d_j}\),也就是\(\frac{d_j}{2m} * \frac{1}{d_j}=\frac{1}{2m}\)
于是\(f[1][j]=\sum\limits_{(u,j)∈e}\frac{1}{2m}=\frac{d_j}{2m}\)
同理:\(f[i][j]=\sum\limits_{(u,j)∈e}\frac{1}{2m}=\frac{d_j}{2m}\)
此时概率相同了。
\(E(x_1+x_2+……+x_n)=\sum\limits_{i=1}^nE(x_i)=\sum\limits_{i=1}^n\sum\limits_{j=1}^kx_i*f[j][i]*a_i\)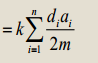
(依照定义还是比较好想的)其中xi表示是否在第i棵苹果树下0/1显然0的情况舍弃;
还有一步化简但是并不想写w
BZOJ4832 抵制克苏恩
你有一个英雄和若干奴隶主,对方每次攻击会从你的英雄和奴隶主中随机选一个造成一点伤害。奴隶主受到攻击后,体力为0则死亡,否则若场上奴隶主少于7个,则召唤一个3点血量的奴隶主。
有T局游戏,每局给出初始奴隶主的数量(<=7)和血量(<=3),给出k,求对方攻击k次后你的英雄受到的总伤害值的期望。
T<=100, k<=50。
设\(f[i][a][b][c]\)表示还要进行i轮攻击,三种血量的奴隶主数量分别为a(血量为1)b(血量2)c(血量3)时,接下来英雄受到的期望总伤害。
设当前共有s=a+b+c个人,那么有1/s的概率打到英雄,a/s的概率打到血量为1的人,b/s的概率打到血量为2的人,c/s的概率打到血量为3的人。
咋的要这样设计状态倒着dp
打到英雄\(f[i-1][a][b][c]+=(f[i][a][b][c]+1)*\frac{1}{s+1};\)
打到a \(f[i-1][a-1][b][c/c+1]+=f[i][a][b][c]*\frac{a}{s+1};\) 此处c考虑奴隶主数是否<7
打到b \(f[i-1][a+1][b-1][c/c+1]+=f[i][a][b][c]*\frac{b}{s+1}\) 此处c考虑奴隶主数是否<7
打到c \(f[i-1][a][b+1][c-1/c]+=f[i][a][b][c]*\frac{c}{s+1}\) 此处c考虑奴隶主数是否<7
NOIP2016 换教室
小A的学校可以视为一个v个点的无向图,他有n门课程要按顺序上课,其中第i门课程要在节点ai进行,但还有一个备选地点bi。
现在小A有m个申请机会,若申请第i门课,那么将有ki的概率使课程搬到bi进行。每门课最多申请一次,而且要在全部申请完成后才知道是否成功,m次机会不必全部用完。他如何申请才能最小化在上课地点间移动的距离的期望值。求该期望值。
v<=300, n,m<=2000
f[i][j][0/1]表示前i个课程申请了j次,且第i个是否申请时的最小期望值。
$f[i][j][0]=Min(f[i-1][j][0]+dis(a[i-1],a[i]) ,
f[i-1][j][1]+k[i-1]dis(b[i-1],a[i])+(1-k[i-1])dis(a[i-1],a[i])) $
\(f[i][j][1]=Min(f[i-1][j-1][0]+dis(a[i-1],b[i])*k[i]+(1-k[i])*dis(a[i-1],a[i]),\\f[i-1][j-1][1]+dis(b[i-1],b[i])*k[i]*k[i-1]+dis(a[i-1]*b[i])*(1-k[i-1])*k[i]\\+dis(b[i-1],a[i])*k[i-1]*(1-k[i])+dis(a[i-1],a[i])*(1-k[i-1])*(1-k[i]));\)
时间复杂度O(v^3+nm)
BZOJ1076 奖励关
有n轮游戏和m种宝物,每种宝物有分数Pi(可以为负),每轮游戏会等概率抛出一种宝物,你可以选择吃或不吃。第i种宝物还有一个限制集合Si,表示只有在Si中的宝物都吃过后,才能吃第i种宝物。
求最优策略下的期望得分。
n<=100, m<=15
设\(f[i][S]\)为还剩下i轮游戏,吃过的宝物集合为S时,接下来能得到的最大期望得分。
==s=--i--
然后同样是倒着搞,最后答案就是当前一轮游戏都没进行,吃过的宝物为0的情况\(f[n][0]\);初始状态是\(f[0][S]\)其中S是全集;
然后枚举第n-i轮游戏是不是吃了宝物;
如果没吃,显然第n-i轮和第n-i+1轮的结果相同,即\(f[i][S]=f[i-1][S]\)
如果吃了宝物,那么显然第n-i+1轮就多了一个宝物,又因为倒着转移,所以第n-i+1轮的结果要并上第n-i轮吃掉的宝物k,并且加上这个宝物的分数。即\(f[i][S]=f[i-1][S|(i<<l-1)]+p[l]\)
合起来:\(f[i][S]=max\{f[i-1][S],f[i-1][S|(i<<l-1)]+p[l]\};\)
网络题解:



