【暑假培训1】test1
T1:

30pts:直接暴力三层循环枚举
就就就先不写代码了qwq;
70pts:
因为X+Y+Z==0
所以我们可以考虑枚举X和Y,然后利用↑式子求出Z=-X-Y;

然后touli xcg的70pts code:

#include<cstdio> #include<iostream> #include<algorithm> #include<cmath> #include<set> using namespace std; int read() { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<3)+(a<<1)+(ch-'0'); ch=getchar(); } return a*x; } int t,n,x,tot,ans; int a[10001]; set<int> st; int main() { freopen("sum.in","r",stdin); freopen("sum.out","w",stdout); t=read(); while(t--) { ans=0;tot=0; st.clear(); n=read(); for(int i=1;i<=n;i++) { x=read(); st.insert(x); } set<int>::iterator it; //定义前向迭代器 for(it=st.begin();it!=st.end();it++) { a[++tot]=*it; //cout<<a[tot]<<' '; } if(tot<3) { printf("0\n"); continue; } for(int i=1;i<=tot;i++) //作为相反数组的第一个数 { if(a[i]>=0) break; for(int j=i+1;j<=tot;j++) //第二个数 { for(int k=j+1;k<=tot;k++) //第三个数 { if(a[k]<=0) continue; if(a[i]+a[j]+a[k]==0) { ans++; break; } } } } printf("%d\n",ans); } return 0; }
100pts:
SOLUTION:
这里对于我们枚举的j和k,我们会发现有很大一部分是浪费了的,当我们排序过后,如果相加的和<0时,我们增大j,当相加>0时,我们令最大的k--;(因为k是从最后开始枚举,所以如果连k和其他两数相加都不能满足和>0,显然我们要使j增大)
然后unique去重;
以下是STD:
#include <cstdio> #include <algorithm> const int numsize = 131072; int T, N; int a[numsize]; inline int getint() { register int num = 0; register char ch = 0, last; do last = ch, ch = getchar(); while (ch < '0' || ch > '9'); do num = num * 10 + ch - '0', ch = getchar(); while (ch >= '0' && ch <= '9'); if (last == '-') num = -num; return num; } int main() { freopen("sum.in", "r", stdin); freopen("sum.out", "w", stdout); T = getint(); for (int i = 0; i < T; i++) { N = getint(); for (int i = 1; i <= N; i++) a[i] = getint(); std::sort(a + 1, a + N + 1); int cnt = 0; N = std::unique(a + 1, a + N + 1) - (a + 1); for (int i = 1; i < N; i++) { int left = i + 1, right = N; while (left < right) { if (a[i] + a[left] + a[right] == 0) { left++; cnt++; } if (a[i] + a[left] + a[right] > 0) right--; if (a[i] + a[left] + a[right] < 0) left++; } } printf("%d\n", cnt); } return 0; }
还有一个我的code,然后用70pts思路过了100%数据就很迷了???

#include<iostream> #include<algorithm> #include<cstdio> #include<cstring> #include<set> #define ll long long using namespace std; inline ll read(){ ll ans=0; char last=' ',ch=getchar(); while(ch>'9'||ch<'0') last=ch,ch=getchar(); while(ch<='9'&&ch>='0') ans=(ans<<1)+(ans<<3)+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } bool cmp(int x,int y){return x<y;} ll n,ans; ll c[1010],fcnt,zcnt,cnt0; bool bj0; ll find(ll x){ int l=0,r=n; int mid; while(l<=r){ mid=l+r>>1; if(c[mid]>x) r=mid-1; else l=mid+1; } if(c[r]!=x) return 0; return 1; } void solve(){ sort(c+1,c+n+1,cmp); ll sum; for(int i=1;i<=n;i++){ if(c[i]==c[i-1]) continue; for(int j=i+1;j<=n;j++){ if(c[i]==c[j]||c[j]==c[j-1]) continue; sum=c[i]+c[j]; if(-sum<=c[i]||-sum<=c[j]) continue; if(sum==0&&bj0==1){ ans++; continue; } ans+=find(-sum); } } } int main(){ freopen("sum.in","r",stdin); freopen("sum.out","w",stdout); int T; scanf("%d",&T); for(int i=1;i<=T;i++){ n=read(); if(n<3){ printf("0\n"); continue; } bool bjf=0,bjz=0; memset(c,0,sizeof(c)); cnt0=0;bj0=0;ans=0; for(int j=1;j<=n;j++){ ll _num=read(); if(_num<0) bjf=1,c[j]=_num; if(_num>0) bjz=1,c[j]=_num; if(_num==0) bj0=1; } if(bjf==0||bjz==0) { printf("0\n"); continue; } solve(); printf("%lld\n",ans); } return 0; }
T2:


看数据范围p<=2*10^6,奇怪?那么我们大胆猜想gi一定<=2*10^6那一定会有gj==gi
那么我们找循环节
两个数组f和g,f数组记录我们所计算的函数值,然后g数组记录这个值第一次出现在哪里。
然后从第二项开始计算,直到计算到n,然后写一个朴素的函数,计算。然后如果我们找到了一个数,之前已经出现过了,那么我们记这个数为循环点,然后弹出;否则记g[f[i]]=i;
然后如果我们还没有找到循环节,就直接输出就可以了;
如果找到循环点了,我们可以令m=第一循环结最前所在项数-1,l=第二个循环的第一个点项数-第一循环结最前点所在项数;
然后先令n-=m;(把不循环的部分减掉)
然后将剩下循环的部分%=l;这样剩下的就是不足一个循环结的问题;
当n==0时,为循环节最后一个,因此令n=l;然后输出f[m+n];
STD:
#include <cstdio> #include <cstring> const int mod = 2097152; int F(long long x, int a, int b, int c, int p) { long long ans = 0; ans = a * x % p * x % p; ans = (ans + b * x % p) % p; ans = (ans + c) % p; return ans; } int g1, a, b, c, p; long long n; int f[mod]; int g[mod]; int main() { freopen("sequence.in", "r", stdin); freopen("sequence.out", "w", stdout); scanf("%d %d %d %d %lld %d", &g1, &a, &b, &c, &n, &p); g1 = (g1 % p + p) % p; a = (a % p + p) % p; b = (b % p + p) % p; c = (c % p + p) % p; //先处理成正数 memset(g, 0, sizeof(g)); f[1] = g1, g[g1] = 1; int point = 0; for (int i = 2; true; i++) { if (i > n) break; f[i] = F(f[i - 1], a, b, c, p); if (g[f[i]]) { point = i; break; } g[f[i]] = i; } if (!point) printf("%d\n", f[n]); else { int m = g[f[point]] - 1, l = point - g[f[point]]; n -= m; n %= l; if (n == 0) n = l; printf("%d\n", f[m+n]); } return 0; }
T3:


考虑整体分治:
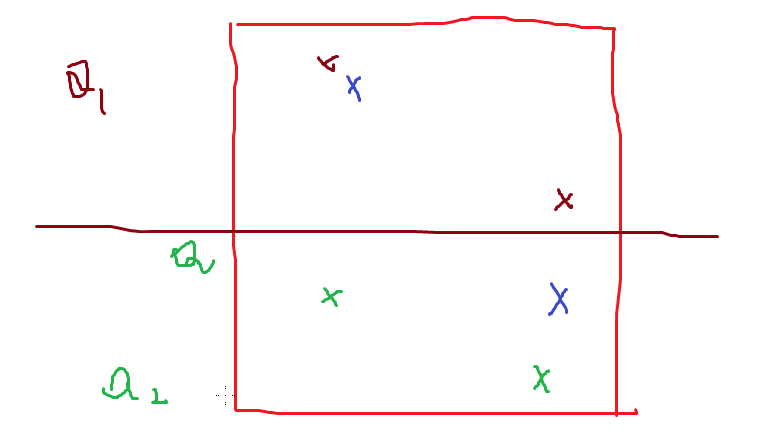
考虑三种情况,一种全在p行之上,一种全在p行之下,还有一种一个在p之上,一个在p之下;
对于全在p行之上和全在p行之下的情况,我们可以直接递归的解决,只需要解决一个在p行之上,一个在p行之下的问题: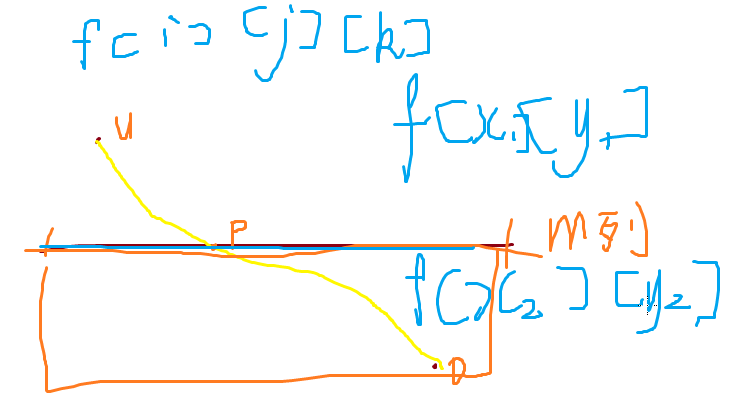
处理01数组处理每个点到第k列的每一点是否可以走到(1为可以,0不可以)然后比较是否有相同
预处理:
凹凸不平: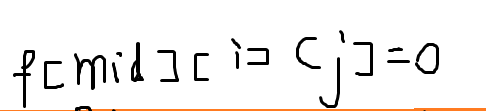
否则记为:

上面乱七八糟的qwq,还是下面比较清晰:


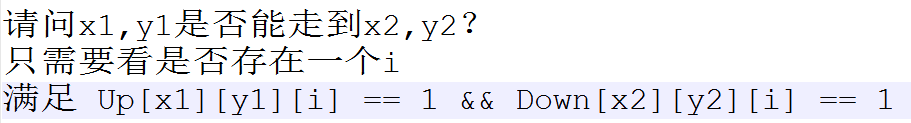
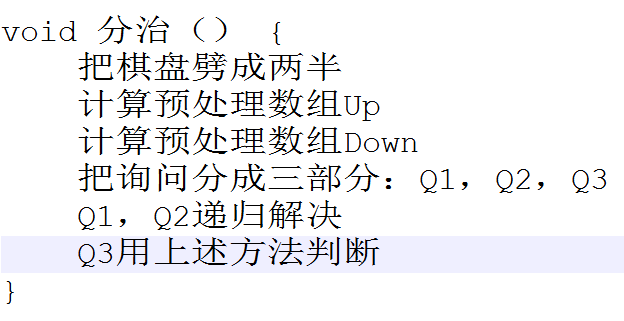
Up的计算

Up往右走能否走通+往下走能否走通,二者满足其一即可:
Down同理
然后如果只存1/0,会爆炸,因此我们压个位。
 比如直接让101011存成一个int43
比如直接让101011存成一个int43
把32位01数组压成一个int/64位long long数组
#include <cstdio> #include <vector> #include <bitset> using std::vector; using std::bitset; const int QUERY_SIZE = 600006; const int MAP_SIZE = 511; int N, M, Q; char map[MAP_SIZE][MAP_SIZE]; int ans[QUERY_SIZE]; bitset<MAP_SIZE> up[MAP_SIZE][MAP_SIZE], down[MAP_SIZE][MAP_SIZE]; struct query { int x1, y1, x2, y2, id; }; query q; void solve(vector<query> v, int l, int r) { int m = (l + r) >> 1; if (l > r) return ; for (int i = m; i >= l; i--) for (int j = M; j >= 1; j--) { up[i][j] = 0; if (map[i][j] == '.') { if (i == m) up[i][j].set(j); else up[i][j] |= up[i + 1][j]; if (j != M) up[i][j] |= up[i][j + 1]; } } for (int i = m; i <= r; i++) for (int j = 1; j <= M; j++) { down[i][j] = 0; if (map[i][j] == '.') { if (i == m) down[i][j].set(j); else down[i][j] |= down[i - 1][j]; if (j != 1) down[i][j] |= down[i][j - 1]; } } vector<query> vl, vr; for (vector<query>::iterator it = v.begin(); it != v.end(); it++) { q = *it; if (q.x2 < m) vl.push_back(q); else if (q.x1 > m) vr.push_back(q); else ans[q.id] = (up[q.x1][q.y1] & down[q.x2][q.y2]).any(); } solve(vl, l, m - 1); solve(vr, m + 1, r); } int main() { freopen("boardgame.in", "r", stdin); freopen("boardgame.out", "w", stdout); scanf("%d %d", &N, &M); for (int i = 1; i <= N; i++) scanf("%s", map[i] + 1); vector<query> v; scanf("%d", &Q); for (int i = 0; i < Q; i++) { scanf("%d %d %d %d", &q.x1, &q.y1, &q.x2, &q.y2); q.id = i; v.push_back(q); } solve(v, 1, N); for (int i = 0; i < Q; i++) puts(ans[i] ? "Yes" : "No"); return 0; }





