【7.9校内test】T1挖地雷

（土气的名字万里挑一丫丫）

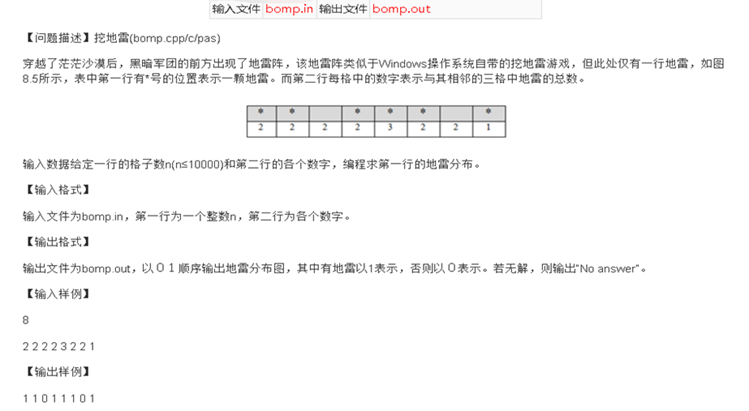
然后这个题是个递推，lz的考场想法：

3个的最好确定，先把3个的确定下来，然后从这个点往前推，从这个点往后推这么算吧qwq

然后码长：也是很nice，最关键的是，我都写的这么复杂了，它居然还是没有ac掉，已经放弃修改这篇(85分代码，不会改了。挂出来求救)代码了qwq（欢迎大佬批评指正，全篇推翻也可以）。

然后题解solution：

首先我们先判断输入的数据是否合法，显然对于每个格子中的数字，只能是0~3之间的数，其它数只要出现就无解。

然后是计算雷，对于a[1]==0||a[1]==2的情况，我们都可以清楚的确定出雷的位置，对于a[1]==3的情况，显然是无解的，而对于a[1]==1的情况，我们需要分1 0和0 1两种情况讨论了。

定义一个int型数组f，表示雷的数量，因为我们有无解的情况，所以可能会出现f[i]<0||f[i]>1的情况，因此不可以开bool数组；

然后根据a[1]的值，先将f[1]f[2]判断出来（对于a[1]==1的情况我们先假定为其中的一种，如果这种情况无解，我们再判断另一种情况）

然后递推：

int dt(){
    for(int i=2;i<=n;i++){
        f[i+1]=a[i]-f[i-1]-f[i];
        if(f[i+1]<0||f[i+1]>1) return 0;
    }
    if(f[n+1]!=0) return 0;
    else return 1;
}

从i=2开始递推，推到i=n；

对于当前位置kk的地雷数，等于上一个位置kk-1的a(因为a数组表示的是本身，+1,-1的总地雷数）-上一个位置kk-1的地雷数-上上个位置kk-2的地雷数；

画个图感性理解一下：

 

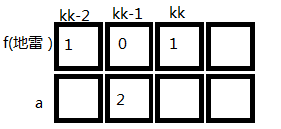
然后当某个位置的雷>1或<0时，显然就炸了，直接进入无解情况。

然后这个递推，会推到f[n+1]，显然如果f[n+1]!=0，也是无解的，因此最后记得判一下；

当a[1]==1并且我们算的第一种情况无解时，我们还需要判断一下第二种情况，所以需要再写一个特判。

CODE：

#include<bits/stdc++.h>

using namespace std;

inline int read(){
    int ans=0;
    char last=' ',ch=getchar();
    while(ch>'9'||ch<'0') last=ch,ch=getchar();
    while(ch<='9'&&ch>='0') ans=(ans<<1)+(ans<<3)+ch-'0',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

int n,aa;
int a[10005],f[10005];

int dt(){
    for(int i=2;i<=n;i++){
        f[i+1]=a[i]-f[i-1]-f[i];
        if(f[i+1]<0||f[i+1]>1) return 0;
    }
    if(f[n+1]!=0) return 0;
    else return 1;
}

int main(){
    n=read();
    for(int i=1;i<=n;i++){
        a[i]=read();
        if(a[i]>3||a[i]<0) {
            printf("No answer");
            return 0;
        }
    }
    
    if(a[1]==3||a[n]==3) {
        printf("No answer");
        return 0;
    }
    if(a[1]==0){
        f[1]=f[2]=0;
    }
    if(a[1]==1){
        f[1]=1;f[2]=0;
    }
    if(a[1]==2){
        f[1]=f[2]=1;
    }
    
    aa=dt();
    
    if(aa==0&&a[1]==1){
        f[1]=0;f[2]=1;
    }
    aa=dt();
    if(aa==0) printf("No answer");
    else {
        for(int i=1;i<=n;i++)
            printf("%d ",f[i]);
    }
    return 0;
}

end-