【洛谷p1058】立体图（已完结）
然后因为有点（不是有点，非常）懵，因此我只能看一步写一步。
首先总体思路：
将三维立体图看做二维平面图，先确定出二维图的长和宽，然后，按照三维立体图的透视顺序，从最后一排的最左开始依次覆盖操作，直到覆盖完成，不用的地方填‘.’；
首先是处理二维图的长和宽：
(首先要说的是，以下所有长均指竖向，宽均为横向）
经过画图找规律我们了解到了对于一个方块，如果我们在它上面增加一个方块，对于这个方块和新增的方块的某个对应点来说，长增加了3，宽增加0；:
对应点用不同颜色标出；
然后对于前后摆放的情况：
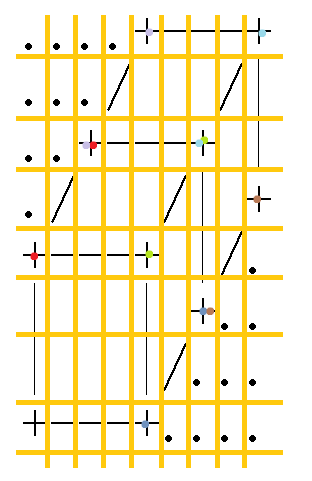
从图中可以看出，长增加了2，宽增加了2；
然后对于左右摆放的情况：
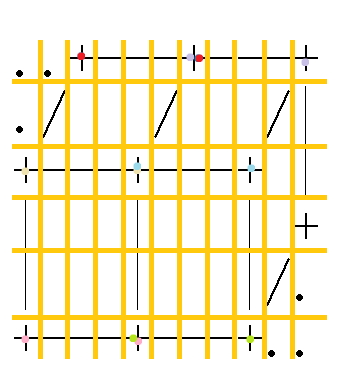
由图中可以看出，长莫得增加，宽增加了4；
然后对应以下数组：
//宽的增加量
int dm[4]={0,0,4,2};//1竖着摞，2横着摞，3前后摞
//长的增加量
int dn[4]={0,3,0,2};//1竖着摞，2横着摞，3前后摞
然后我们求一下我们要存的二维平面的大小：
对于横放的宽：从最左下角开始计算，先计算
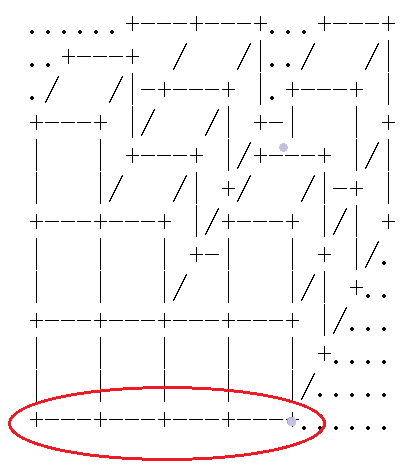中，最右下的位置（图中红圈内紫色点的位置）；
=（m-1）*dm[2]+5（首先第一个方块占了5个单位，然后剩余的m-1个方块，每放一个，增加4个单位）
计算完成后，再计算
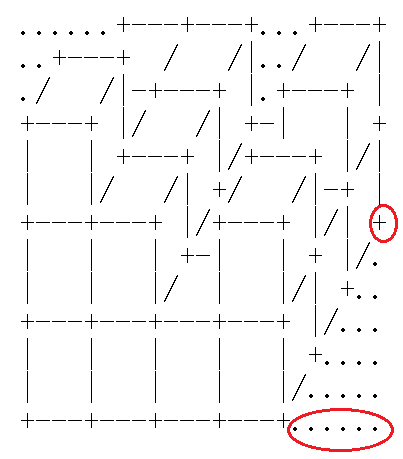中剩余位置也就是红圈‘+’所在位置，如何计算剩下的长度呢，我们需要用到前后摆放的增加量：还是同样，首先先把第一个方块单列，这个方块的（右面吧）为宽提供了3的价值（但是要注意的是，因为第一个方块最左下的贡献与上面的计算重复了，所以实际我们只需要+2），剩余n-1个方块，每个为宽提供了2个价值。
因此宽mm=5+(m-1)*dm[2]+(n-1)*dm[3]+2；
再来看长，因为lz看的题解的博主：小蒟蒻皮皮鱼（友情安利，这是个大佬）他自己说他比较菜，用的枚举的方法，lz也只看懂了枚举的方法：
for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) nn=max(nn,atlas[i][j]*dn[1]+dn[3]*(n-i+1)+1); //枚举每一个点的长，取最大值
同样算最高的，先算出：atlas[i][j]*dn[1]+1（其中atlas为输入的矩阵数据），算出的是粉线部分，然后(n-i+1)这个表示的是第几排（因为数组是：↓→这样存储的，但是实际上我们要画的是↑→的图，因此要减一下）对于第（n-i+1）排，它的上面对长的贡献就是dn[3]*（n-i+1）（这里不再加一是因为有一个点前面和上面都有贡献，我们只需要加一次（绿点处）），也就是每个方块对长贡献2；（当然要枚举取最高的）
然后考虑一张图，我们按照透视的顺序，从后往前，从左往右的依次添加覆盖，首先是最左下的立方体（其实一般会被全部覆盖掉，但我们还是要加），然后我们固定一个点，为立方体的定位点，以此点为基础拓展出整个立方体，所以最关键的一点就是定位立方体了：
这里定位立方体的左下角：
然后就是咋的定位了，
然后我们还是看个样例：（啊算了，我补不出来（艰难））
（百度网图qwq）
然后你看这个图，输入的数据中为atlas[1][1]的立方体的左下角就是红点标出的地方，然后我们求出的nn是绿色线标出的地方，mm是紫色线标出的地方，这样我们在存二维数组时，先存最左下角的立方体：
求某个立方体左下角坐标：
对于x（与nn（长）同方向的那个），我们显然只需要考虑dn对其的影响；（上下）
然后因为我们的思路是：
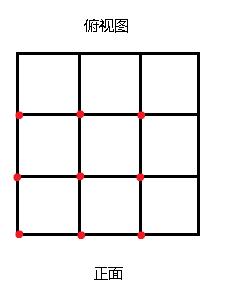求出红点的在二维平面的坐标，然后给对于每个立方体上面再摞立方体。
所以不用把层数>=2的左下角求出来；
回到这个图：
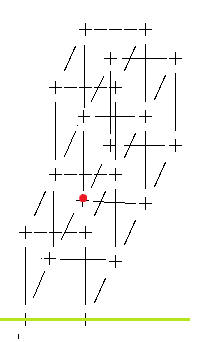
我们应该如何求这个点的x呢？？
先放代码（因为发现莫得代码不知道咋的讲）：
for(int i=1;i<=n;i++){ for(int j=1,x,y;j<=m;j++){ x=nn-dn[3]*(n-i); y=dm[3]*(n-i)+dm[2]*(j-1)+1; zhetizhenduliu(i,j,x,y); } }
根据我们楼上的经验，对于每一横行来说，每向后放置一个立方体，对应点的x就会+dn[3]，因此我们在计算x时，考虑这个立方体相对于第一排立方体向后挪了几个，因为数组atlas[1][i]其实对应的是最后一行，所以我们覆盖是从1↓m，1→n。（n-i）表示的就是我们从第一行向后放了几个立方体到达了我们当前要放立方体的这一行，楼上红点就是3-1，表示我们在放这个方块之前已经放了两个方块，每放一个方块，x就要相对于绿线 所在地方向后dn[3]（2）个，因为绿线是最大的位置，所以实际我们需要用nn-（n-i）*dn[3]；
然后对于y（与mm方向相同）（宽）
啊又要画图
还是先推第一排的立方体，假设j=2（先不管i了在这不重要）
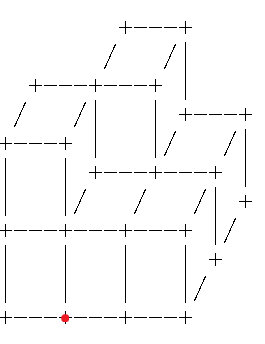
那么很显然这个点首先要计算的还是第一排的位置，也就是(j-1)*dm[2]+1(每左右放一个方块增加4，因为我们求的是左下角，所以不能用j乘而是要用(j-1)乘（然后别忘了+1）。
然后再算前后摆放造成的影响，也是同样，对于前后摆放，每摆放一个，左下角的位置向右挪2，然后也是从后往前记得编号嘛，所以还是要用(n-i)*dm[3];
然后定位好了左下角，我们可以尝试开始覆盖了：
inline void zhetizhenduliu(int i,int j,int x,int y){ //x,y表示我们定位点的左下角坐标，i,j表示我们定位点应该是输入矩阵的哪一个坐标； int a,b; while(atlas[i][j]--){ for(a=0;a<6;a++) for(b=0;b<7;b++) if(s1[6-a-1][b]!='.') s[x-a][y+b]=s1[6-a-1][b]; x-=3; } }
然后忘记讲的一件事，我们要先将立方体打好表：
char s1[6][8]= { "..+---+", "./ /|", "+---+ |", "| | +", "| |/.", "+---+.." };//真好看的说
然后你看这是个6*7的表，但开了6*8，你开6*7会炸，因为对于字符串， 除了你存的字符外，它会再存入一个我也忘了叫啥的某个东西，因此我们要多开一个；
然后覆盖：
首先要讲的是，我们只计算了最底层的立方体的左下角位置，然后是向上摞立方体，当我们每向上摞一个立方体时，长就 -=3；（因为我们输出是从上往下输出，所以越靠近输出的最上方的立方体的长其实越小，也就是需要 -=3而不是+=3的原因）这是最外层while循环；
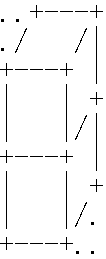
我们计算出来的(x,y)实际上对应到s1数组中是s1[6][0]；
用s数组存最终覆盖后的答案，那么注意要判断的是s1[i][j]（表示s1数组中某一个位置）!='.'或许你会像我一样开始时认为没什么用，但是如果你不加这一句：
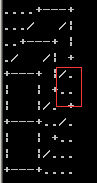你就wa声一片了；
注意的是，这里s数组是从1开始存的，而s1数组是从0开始存的；
然后应该可以理解的吧，因为我们定位的是左下角，所以对于其他任意一个点，都可以由左下角的点的坐标加加减减得出，而且对于长，一定是减，对于宽，一定是加（加减均包括0），然后就枚举就好啦；
附上ych小蒟蒻皮皮鱼的神仙代码：
#include<iostream> #include<cstdio> #include<cstdlib> #include<cstring> #include<string> #include<algorithm> #include<cmath> #include<queue> using namespace std; inline int read() { int ans=0; char last=' ',ch=getchar(); while(ch<'0'||ch>'9') last=ch,ch=getchar(); while(ch>='0'&&ch<='9') ans=(ans<<1)+(ans<<3)+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } int n,m; char s1[6][8]= { "..+---+", "./ /|", "+---+ |", "| | +", "| |/.", "+---+.." }; int dm[4]= {0,0,4,2}; int dn[4]= {0,3,0,2}; char s[1000][1000]; int atlas[51][51]; int mm,nn; inline void zhetizhenduliu(int i,int j,int x,int y) { int a,b; while(atlas[i][j]--) { for(a=0; a<6; a++) for(b=0; b<7; b++) if(s1[6-a-1][b]!='.') s[x-a][y+b]=s1[6-a-1][b]; x-=3; } } int main() { n=read(),m=read(); for(int i=1; i<=1000; i++) for(int j=1; j<=1000; j++) s[i][j]='.'; for(int i=1; i<=n; i++) for(int j=1; j<=m; j++) atlas[i][j]=read(); mm=7+(n-1)*dm[3]+(m-1)*dm[2]; for(int i=1; i<=n; i++) for(int j=1; j<=m; j++) nn=max(nn,atlas[i][j]*dn[1]+dn[3]*(n-i+1)+1); for(int i=1; i<=n; i++) { for(int j=1,x,y; j<=m; j++) { x=nn-dn[3]*(n-i); y=dm[3]*(n-i)+dm[2]*(j-1)+1; zhetizhenduliu(i,j,x,y); } } for(int i=1; i<=nn; i++) { for(int j=1; j<=mm; j++) { printf("%c",s[i][j]); } puts(""); } return 0; }
end-
