线段树小记
日常废话:
不知道为什么对water_lift的线段树板子有着迷之执着,就是想用water_lift的板子。(但是忘记water_lift怎么写的了然后又找不到类似的板子只能与一本通为伍了qwq)
线段树?是什么:
线段树是一种数据结构,用来维护一段区间的某个特征(比如最小值、和、积……)的二叉树。最简单的应用大概就是求和、维护最小值一类,当然线段树复杂起来让你想象不到。
线段树的几个基本操作:
以求区间和的区间查询,单点修改,区间修改为eg
首先的说,其实本来想先写一个朴素的会炸的区间修改的,结果我不会emm,所以直接加lazy_tag了。
Lazy_tag:
延迟标记,如果区间修改时我们递归到叶节点在进行修改的话,复杂度是O(mlogn),比朴素还要慢,因此有延迟下传的标记,当我们暂时用不到此子树时,不需进行更新,只需要在树根上打一个标记,然后维护此根节点的值。当用到此子树时,再进行下传。
假装所有的基本操作都已经写好了:
#include<bits/stdc++.h> #define ll long long using namespace std; inline ll read(){ ll ans=0; char last=' ',ch=getchar(); while(ch>'9'||ch<'0') last=ch,ch=getchar(); while(ch>='0'&&ch<='9') ans=(ans<<1)+(ans<<3)+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } const ll N=100005; ll n,m; ll val[N]; ll sum[N*4],laz[N*4]; int main(){ n=read();m=read(); for(int i=1;i<=n;i++) val[i]=read(); build(1,1,n); ll ops,x,y,k; for(int i=1;i<=m;i++){ ops=read();x=read();y=read(); if(ops==1){ k=read(); Add(1,1,n,x,y,k); } else printf("%lld\n",query(1,1,n,x,y)); } return 0; }
1.建树;
“你在写什么啊?”
“线段树。”
“树呢?”
没有树的线段树是没有灵魂的,因此第一步显然是建树;(大概我只会写建树了)
建树代码:
void build(ll node,ll x,ll y){ if(x==y){ sum[node]=val[x]; return; } ll mid=x+y>>1; build(node<<1,x,mid); build(node<<1|1,mid+1,y); sum[node]=sum[node<<1]+sum[node<<1|1]; }
解释一下:
ll node表示当前要建的结点编号,ll x表示此区间的左端点,ll y表示此区间的右端点;
当x==y时,也就是叶子结点,非常容易就可以知道此结点的sum就是它本身的值。
然后因为线段树是非常严格的二叉树,因此它的每个儿子的编号都是确定的,分别为node*2和node*2+1;因此递归的建树,最后维护区间和就好了;
2.区间查询操作:
先上代码:
ll query(ll node,ll l,ll r,ll x,ll y){ if(l>=x&&r<=y)//递归到的区间完全被包含在要查询区间中 return sum[node]; ll mid=l+r>>1; ll res=0;
pushdown(node,l,r,mid); if(x<=mid) res+=query(node<<1,l,mid,x,y); if(mid<y) res+=query(node<<1|1,mid+1,r,x,y); return res; }
解释一波:
因为查询时一定是从1~n开始查询,然后递归查询。所以当递归到一个完全被包含在要查询区间的数,显然可以不用向下继续递归了,因为这个点已经维护了这段区间的和,直接返回就可以;然后判断区间中点,显然如果出现:
x<=mid的情况,也就表示我们可以在node 的左儿子中查询到一个区间(区间的大小我们无法确定,可能是整个左儿子,也可能是左儿子的一个叶节点),那么就需要去递归的求左儿子
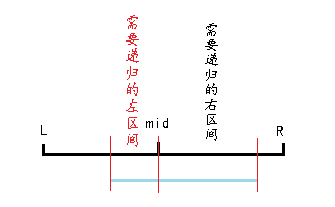
y>mid的情况,也就说明在右儿子中一定包含一部分是在区间[x,y]中,所以需要递归右儿子;
然后将左儿子和右儿子递归到的值加起来,就是我们要查询的区间的和;
3.单点修改(不会写需现学)
CODE:
void change(ll node,ll l,ll r,ll x,ll v){//单点加v if(r<x||l>x) return;//当右区间比要修改的x的值要小时,显然递归右区间没有用 //左区间同理 if(l==r&&l==x){ sum[node]+=v; return; } ll mid=l+r>>1; change(node<<1|1,mid+1,r,x,v); change(node<<1,l,mid,x,v); sum[node]=sum[node<<1]+sum[node<<1|1]; }
解释一波~
首先判断不可能有解的情况:当前递归到的区间的最右要比x小时
 显然再递归下去也不可能找到解,所以直接return好啦;
显然再递归下去也不可能找到解,所以直接return好啦;
同样当递归到的区间的最左比x大时,显然也不行:
因此这两种情况都直接return;
当递归到了我们需要修改的x时:修改对应sum值,返回。
然后对于不是需要修改的x但是将x包含在内的区间,我们分别递归的求它的左右儿子,最后还有重新维护sum的值;
4.区间修改:
先上代码++:
void add(ll node,ll l,ll r,ll k){ laz[node]+=k; sum[node]+=(r-l+1)*k; } void pushdown(ll node,ll l,ll r,ll mid){ if(laz[node]==0) return; add(node<<1,l,mid,laz[node]); add(node<<1|1,mid+1,r,laz[node]); laz[node]=0; } void Add(ll node,ll l,ll r,ll x,ll y,ll k){ if(x<=l&&y>=r) return add(node,l,r,k); ll mid=l+r>>1; pushdown(node,l,r,mid); if(x<=mid) Add(node<<1,l,mid,x,y,k); if(y>mid) Add(node<<1|1,mid+1,r,x,y,k); sum[node]=sum[node<<1]+sum[node<<1|1]; }
开始解释:
首先判断,如果当前的递归区间完全包含在区间[x,y]中,直接对这个区间进行add操作,维护这个区间的区间和,然后打lazy_tag;

然后还是相应的分别递归左儿子和右儿子,还是相应的判断是否需要递归。最后不要忘记维护区间的和。
然后确实没有搞明白为啥此时要pushdown。
pushdown就是标记下传的过程;
CODE:
#include<bits/stdc++.h> #define ll long long const int N=100005; using namespace std; inline ll read(){ int ans=0; char last=' ',ch=getchar(); while(ch>'9'||ch<'0') last=ch,ch=getchar(); while(ch<='9'&&ch>='0') ans=(ans<<3)+(ans<<1)+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } ll n,m; ll val[N],sum[N*4],laz[N*4]; void build(ll node,ll x,ll y){//建树 if(x==y){ sum[node]=val[x]; return; } ll mid=x+y>>1; build(node<<1,x,mid); build(node<<1|1,mid+1,y); sum[node]=sum[node<<1]+sum[node<<1|1]; } void add(ll node,ll l,ll r,ll k){//添加维护 laz[node]+=k; sum[node]+=(r-l+1)*k; } void pushdown(ll node,ll l,ll r,ll mid){//标记下传 if(laz[node]==0) return; add(node<<1,l,mid,laz[node]); add(node<<1|1,mid+1,r,laz[node]); laz[node]=0; } ll query(ll node,ll l,ll r,ll x,ll y){//查询 if(l>=x&&r<=y)//递归到的区间完全被包含在要查询区间中 return sum[node]; ll mid=l+r>>1; ll res=0; pushdown(node,l,r,mid); if(x<=mid) res+=query(node<<1,l,mid,x,y); if(mid<y) res+=query(node<<1|1,mid+1,r,x,y); return res; } void change(ll node,ll l,ll r,ll x,ll v){//单点加v if(r<x||l>x) return;//当右区间比要修改的x的值要小时,显然递归右区间没有用 //左区间同理 if(l==r&&l==x){ sum[node]+=v; return; } ll mid=l+r>>1; change(node<<1|1,mid+1,r,x,v); change(node<<1,l,mid,x,v); sum[node]=sum[node<<1]+sum[node<<1|1]; } void Add(ll node,ll l,ll r,ll x,ll y,ll k){//区间加k if(x<=l&&y>=r) return add(node,l,r,k); ll mid=l+r>>1; pushdown(node,l,r,mid); if(x<=mid) Add(node<<1,l,mid,x,y,k); if(y>mid) Add(node<<1|1,mid+1,r,x,y,k); sum[node]=sum[node<<1]+sum[node<<1|1]; } int main(){ n=read();m=read(); for(ll i=1;i<=n;i++) val[i]=read(); build(1,1,n); int ops; ll x,y,k; for(ll i=1;i<=m;i++){ ops=read(); x=read();y=read(); if(ops==1){ k=read(); Add(1,1,n,x,y,k); } else printf("%lld",query(1,1,n,x,y)); } return 0; }
对了注意开空间要开序列长度N的4倍,为啥我也不是很清楚,反正不能开二倍。
好了没有了
end-




