【6.20校内test】
反正考的不是很好吧,赶脚炸了啊qwq
然后这两天一直在忙一些神奇的事情,所以没有整理完
手动@water_lift
T1:大美江湖:
【题目背景】
细雪飘落长街,枫叶红透又一年
不只为故友流连,其实我也恋长安
听门外足音慢,依稀见旧时容颜
故事几经悲欢,结局都与你有关
——银临《大美江湖》 【问题描述】
扶苏听着《大美江湖》,在剑三里控制着他的人物炮姐来到了长安。
长安城中有一个任务,需要扶苏进入地下的机关道,机关道是一个 n×m 的矩形地 图,里面有一些怪物和药水。扶苏操控着炮姐在机关道中游荡。有些时候他希望问问你 他的角色有多少攻击力、防御力以及丢失了多少血量。
具体的,在输入文件中会给出一个 n×m 的矩形地图,地图中第 i 行第 j 列的字符 Ci,j 代表机关道中第 i 行第 j 列的元素是什么。具体的,Ci,j∈{‘.’, ‘R’, ‘Q’, ‘Y’, ‘M’}。
其中,
1、字符 . 代表此处可以通过,且无其他元素
2、字符 R 代表此处为生命药水,可以减少炮姐 10 点丢失的血量 HP
3、字符 Q 代表此处为力量药水,可以增加炮姐 5 点攻击力 ST
4、字符 Y 代表此处为防御药水,可以增加炮姐 5 点防御力 DE
5、字符 M 代表此处为怪物,炮姐会损失相应血量
每只怪物都有三个参数来描述他们的属性,分别是血量 HPenemy,攻击力 STenemy,防 御力 DEenemy。且所有怪物的属性都相同。
一旦走到怪物格,遭遇战将开始。扶苏一定会打死怪物,怪物对炮姐造成的伤害为:
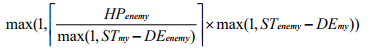
(忍不住说这个数据有点水,我看错括号代码锅掉了居然还A了qwq)
其中 max(a,b) 代表取 a 和 b 的最大值; 的值为不小于 x 的最小整数;下标为 enemy 的参数代表怪物的参数,下标为 my 的参数代表炮姐的参数 你会收到 q 次操作,每次操作要么是一次查询,要么是一次移动。 对于移动,你会再获得一个数字参数,这个参数只可能是 1/2/3/4 其中的一个,代表 炮姐向地图的 左/右/上/下 移动。
的值为不小于 x 的最小整数;下标为 enemy 的参数代表怪物的参数,下标为 my 的参数代表炮姐的参数 你会收到 q 次操作,每次操作要么是一次查询,要么是一次移动。 对于移动,你会再获得一个数字参数,这个参数只可能是 1/2/3/4 其中的一个,代表 炮姐向地图的 左/右/上/下 移动。
【输入格式】 输入文件名为 mzq.in。
输入文件中有且仅有一组数据,第一行为两个正整数 n 和 m,代表地图的大小
下面 n 行,每行 m 个字符,描述机关道的地图
下面一行有三个正整数,分别代表HPenemy,STenemy,DEenemy
下面一行有两个整数 x, y,代表炮姐初始在 第 x 行第 y 列出发。如果出发点有怪物,不发生战斗,如果有道具,不会将其捡拾。
下面一行给出两个正整数,代表炮姐初始的 ST 和 DE。
下面一行给出一个整数 q,代表操作个数
以下q行,每行首先有一个数字,如果是 1,则代表一次查询。否则数字一定是 2, 代表炮姐的一次移动,一个空格后会给出一个数字,作为移动的参数。
【输出格式】
输出文件名为 mzq.out。 对于每个查询,输出一行三个用空格隔开的整数,代表炮姐损失的血量 HP,当前 的攻击力 ST,以及当前的防御力 DE
【输入样例#1】
5 5
MMMMM
RRRRR
QQQQQ
YYYYY
.....
5 5 5
5 1
10 10
8
2 3
1
2 3
2 3
2 3
1
2 2
1
【输出样例#1】
0 10 15
1 15 15
2 15 15
注意:如果多次进入同一个格子,格子上的药水可以重复拾取,小怪会重复出现
注意:如果在拾取药水的时候人物损失的生命值低于10,则会将损失的生命值降至0
SOLUTION:
这道题其实只要直接模拟就好啦,然后注意到一些细节,注意动态维护伤害就好啦
然后其实自己的代码出锅了,所以各位大兄弟看看代码就好啦。
对了还有ceil不要随便用: 点这里吧

#include<iostream> #include<algorithm> #include<cstdio> #include<cstring> #include<cmath> #include<cstdlib> #include<bits/stdc++.h> using namespace std; inline int read(){ int ans=0; char last=' ',ch=getchar(); while(ch<'0'||ch>'9') last=ch,ch=getchar(); while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } int n,m,hp,st,de,sh,x,y,stm,dem,q,cz,hps,yd; int dx[5]={0,0,0,-1,1}; int dy[5]={0,-1,1,0,0}; char a[101][101]; int sx(){ int f=max(1,stm-de); int g=hp/f; if(hp%f!=0) g++; int z=max(1,g); int a=max(1,st-dem); int y=z*a; return y; } //%%%zay int main(){ freopen("mzq.in","r",stdin); freopen("mzq.out","w",stdout); n=read();m=read(); for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++) a[i][j]=getchar(); getchar(); } hp=read();st=read();de=read(); x=read();y=read(); stm=read();dem=read(); q=read(); for(int i=1;i<=q;i++){ cz=read(); if(cz==1) cout<<hps<<" "<<stm<<" "<<dem<<endl; else { yd=read(); x+=dx[yd]; y+=dy[yd]; if(a[x][y]=='M'){ hps+=sx(); } if(a[x][y]=='R'){ if(hps<10) hps=0; else hps-=10; } if(a[x][y]=='Q'){ stm+=5; } if(a[x][y]=='Y'){ dem+=5; } if(a[x][y]=='.'){ continue; } } } return 0; }

#include <cmath> #include <cstdio> #include <algorithm> const int maxn = 110; char mp[maxn][maxn]; int n, m, px, py, q; struct Character { int HP, ST, DE; int ehp, est, ede; void print() { printf("%d %d %d\n", this->HP, this->ST, this->DE); } void fight() { int x = int(ceil(1.0 * ehp / std::max(1, ST - ede))); this->HP += std::max(1, x * std::max(1, est - DE)); } void update(const char x) { switch (x) { case 'R': { this->HP = std::max(0, this->HP - 10); break; } case 'Q': { this->ST += 5; break; } case 'Y': { this->DE += 5; break; } case 'M': { fight(); break; } } } }; Character my; void mov(const int x); int main() { freopen("mzq.in", "r", stdin); freopen("mzq.out", "w", stdout); scanf("%d%d", &n, &m); for (int i = 1; i <= n; ++i) { scanf("%s", mp[i] + 1); } scanf("%d%d%d", &my.ehp, &my.est, &my.ede); scanf("%d%d", &px, &py); scanf("%d%d", &my.ST, &my.DE); scanf("%d", &q); int x; while (q--) { scanf("%d", &x); if (x == 1) { my.print(); } else { x = 0; scanf("%d", &x); mov(x); } } return 0; } void mov(const int x) { switch (x) { case 1: { --py; break; } case 2: { ++py; break; } case 3: { --px; break; } case 4: { ++px; break; } default: { puts("I AK IOI"); break; } }; my.update(mp[px][py]); }
然后T2:腐草为萤
【题目背景】
纤弱的 淤泥中妖冶
颓废在 季夏第三月
最幼嫩的新叶 连凋零都不屑
何必生离死别
——银临《腐草为萤》
【问题描述】
扶苏给了你一棵树,这棵树上长满了幼嫩的新叶,我们约定这棵树的根是 1,每个节 点都代表树上的一个叶子。
如果你不知道什么叫树,你可以认为树是一个边数比节点个数少 1 的无向连通图。 我们如果约定节点 u 是树 T 的根,则可以定义一个节点 v 到根的路径为该无向图上 u, v 两个节点之间的简单路径上的节点集合(包括路径的两个端点)。可以证明,这样的简单路 径只有一条。
我们定义节点 x 是节点 y 的祖先(x y),当且仅当 x 在 y 到根的路径上。
现在扶苏想在这棵树上选定一个集合,将其称之为幼嫩集合,来比较集合中的节点 哪个最幼嫩。注意到一旦集合中存在两个节点 u, v,使得 u 是 v 的祖先,那么一定 v 要比 u 更幼嫩,因为 v 是在 u 的枝丫上生长出来的,那么这样的集合就是没有意义的。也就是 说,扶苏所选择的集合一定满足要求“对于任意集合中的元素对 (u, v),u 不是 v 的祖 先”。
扶苏其实对这些节点哪个最幼嫩并不感兴趣,也对他能选出多少集合不感兴趣,因 为这些都是为了问你下面的问题而创造出的题目背景。
扶苏给每个节点都定义了一个权值,具体的,我们会给出一个参数 T,规定 i 号节点 的权值为 i T。
我们定义一个幼嫩集合幼嫩指数为集合内节点的权值和。现在扶苏想请问你,对于 他所有可能选出的集合,这些集合的幼嫩指数之和是多少。
为了避免答案过大,请你输出答案对 10 7 9 取模的结果。
【输入格式】
输入文件名为 dzy.in。 输入文件中有且仅有一组数据,第一行为两个正整数 n 和 T,节点个数和权值参 数。 下面 n-1 行,每行有两个正整数 u, v,代表树上有一条边连接节点 u 和节点 v。
【输出格式】
输出文件名为 dzy.out。 输出一行一个正整数,代表答案对 10 7 9 取模的结果。
【输入样例 】
5 0
1 2
2 3
2 4
1 5
【输出样例】
16
然后是SOLUTION:
子任务 1:
只有一个点,所以只有 {1} 这一种集合,于是答案为 1。
子任务 2、3:
爆搜,枚举所有可能的集合,然后计算答案。(然鹅我菜到并不会爆搜qwq)
由于每个点只有选进集合或不选两种可能,所以一共有 2 n 个集合,然后可以 O(n) 的去检验集合是否合法,顺便统计答案。于是总复杂度 O(2 n×n)。
子任务 4、5:
考虑 DP。设 fu 是以 u 为根的子树的答案。
first.如果 u 没有孩子,那么 fu = u T。
second.如果 u 只有一个孩子 v,那么要么选 u 不选 u 的子孙,要么不选 u。不选 u 的答案即为 fv,选 u 的答案即为 u T。两种情况加起来就是 fu。
third.如果 u 有两个孩子 x,y。考虑要么选 u,要么只选 x 的子树内的元素,要么 只选 y 的子树内的元素,要么既选 x 内的元素又选 y 内的元素但不选 u。前三种 情况的答案易得。现在考虑第四种情况的答案。设 s 是 x 子树内的某个集合。考 虑无论 y 的子树内怎么选,再加上 s 都是合法的,因为 y 和 x 之间没有祖先后 代关系且 s 在 x 之内。设 gu 是以 u 为根能选择的集合个数,那么一共有 gy 个 集合选择 s 以后依旧合法,设 s 的权值和为 ws,于是 s 的贡献即为 ws×gy。由于 fx 为 x 子树内所有可能集合的权值和,所以可以发现 Σ ws= fx 。于是 x 子树内 的集合对答案的总贡献是 fx×gy。同理,y 子树内的集合对答案的贡献是 fy×gy。 于是 fu=fy×gx+fx×gy+fx+fy+uT。gu=gx×gy+gx+gy+1。时间复杂度O(n)。
子任务6、7:
考虑在遍历子节点的时候,已经遍历了一些子节点,现在新加入了一个子节点。 由于新加入一个子节点与之前遍历的子节点没有祖先后代关系,于是可以之前遍历 过得子树看成一棵子树,然后问题就变成了子任务4、5。
需要注意的是由于读入规模达到了10e6左右,需要普通的读入优化。
(所以其实难写的是代码)

#include <cstdio> typedef long long int ll; const int maxn = 1000005; const int MOD = 1000000007; template <typename T> inline void qr(T &x) { char ch; do { ch = getchar(); } while ((ch > '9') || (ch < '0')); do { x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar(); } while ((ch >= '0') && (ch <= '9')); } int n, T; int MU[maxn], frog[maxn], gorf[maxn]; bool vis[maxn]; struct Edge { int v; Edge *nxt; Edge(const int _v, Edge *h) : v(_v), nxt(h) {} }; Edge *hd[maxn]; void dfs(const int u); int main() { freopen("dzy.in", "r", stdin); freopen("dzy.out", "w", stdout); qr(n); qr(T); if (T) { for (int i = 1; i <= n; ++i) { MU[i] = i; } } else { for (int i = 1; i <= n; ++i) { MU[i] = 1; } } for (int i = 1, u, v; i < n; ++i) { u = v = 0; qr(u); qr(v); hd[u] = new Edge(v, hd[u]); hd[v] = new Edge(u, hd[v]); } dfs(1); printf("%d\n", frog[1] % MOD); return 0; } void dfs(const int u) { vis[u] = true; for (auto e = hd[u]; e; e = e->nxt) if (!vis[e->v]) { int v = e->v; dfs(v); frog[u] = (frog[u] * (gorf[v] + 1ll) % MOD) + (frog[v] * (gorf[u] + 1ll) % MOD); gorf[u] = (gorf[u] + gorf[v] + (1ll * gorf[u] * gorf[v])) % MOD; } frog[u] = (frog[u] + MU[u]) % MOD; ++gorf[u]; }
然后关于读入优化:
- 1e4 cin
- 1e5 scanf
- 1e6 getchar(也就是平常写的快读)
- 1e7 fread
- 1e8及以上 emm,再见!
T3:锦鲤抄
【题目背景】
你在尘世中辗转了千百年
却只让我看你最后一眼
火光描摹容颜燃尽了时间
别留我一人,孑然一身
凋零在梦境里面。
——银临&云の泣《锦鲤抄》
【问题描述】
这首歌的文案讲述了这样一个故事:
在一个兵荒马乱的年代,有一位画师叫浅溪,非常喜欢画锦鲤。战火烧到了泰 安,他的邻居都惊慌逃命,只有他不舍得池中锦鲤没有离开。这天晚上庭院失火, 池中的锦鲤化妖,用生命护住了画师的平安。
注意:由于本题题面涉及到文案故事,在下方提供了便于理解的另一题面版本。
扶苏被画师和锦鲤的故事深深地打动了。为了能让锦鲤和画师继续生活在一起,他 决定回到着火的庭院中灭掉大火。
画师的庭院可以抽象成一个有向图,每个点代表着一个着火的位置。为了量化火势 的大小,扶苏给每个点一个火力值,火力值越大,代表这个点的火势越强。风助火势, 火借风力,对于每一个着火点,都有可能因为大风使得火扩散到其他点。有向图的每条 边 <u,v> 代表大火是从点 u 扩散到点 v 的。需要注意的是一个点可能会扩散到很多 点,也可能是由很多点的大火一起扩散成的。为了不因为灭掉火源让画师发现有人在帮 他灭火,在任意时刻,扶苏不能灭掉任何一个不被任何点所扩散的点的火。一个点的火 被灭掉后,所代表该点的火扩散的所有边将消失。需要说明的是,虽然边消失了,但是 该点扩散到的所有点属性除入度以外都不会改变,更不会消失。
因为穿越的时间有限,扶苏只能灭掉最多 k 个点的火。忙着写题面的扶苏没有时间 算出他最多能扑灭多少火力值,于是他把这个问题交给了你。
便于理解的题面版本:
给你一张有向图,每个点有一个点权。你可以任意选择一个有入度的点,获得它的 点权并把它和它的出边从图上删去。任意时刻不能选择没有入度的点。最多能选择 k 个 点,求最多能获得多少点权。
【输入格式】
输入文件名为 zay.in。
输入文件中有且仅有一组数据,第一行为三个正整数 n,m,k,代表有向图的点数、 边数以及最多选择的点数。
第二行有 n 个整数,第 i 个整数代表节点 i 的火力值(点权)
下面 m 行,每行两个正整数 u,v,代表大火是从 u 扩散到 v 的,即有向图的边。
【输出格式】
输出文件名为 zay.out。
输出一行一个正整数,代表答案。
【输入样例】
7 7 3
10 2 8 4 9 5 7
1 2
1 3
1 4
2 5
3 6
3 7
4 7
【输出样例】
24

SOLUTION:
子任务 1:
点权都是0,于是无论怎么选答案都是 0,输出 0 即可。
子任务 2:
爆搜,枚举所有可能的顺序,然后计算答案。
由于保证了数据随机,可以在搜索的过程中进行剪枝,效率很高。
(不会写qwq)
子任务 3:
给出的是一个 DAG 。考虑对于一个 DAG 来说,一个良好的的性质就是在拓扑 序后面的点无论如何变化都无法影响到前面的点。这个题也一样。对于任意一个不 出现原图中本身入度为 0 的点的序列,只要按照拓扑序选点,就一定能取遍序列中 所有的点。
于是发现这张图上入度不为0的点事实上都可以被选择。于是我们把所有入度不 为0的点排一下序,求前k个就可以了。时间复杂度 O(nlogn)

#include<bits/stdc++.h> using namespace std; inline int read(){ int ans=0; char last=' ',ch=getchar(); while(ch<'0'||ch>'9') last=ch,ch=getchar(); while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } struct node{ int next,to; }edge[500005]; bool cmp(int x,int y){ return x>y; } int head[500005],du[500005],a[500005]; int n,m,k,cnt,u,v,ans; void add(int from,int to){ edge[++cnt].next=head[from]; edge[cnt].to=to; head[from]=cnt; } int main(){ n=read();m=read();k=read(); for(int i=1;i<=n;i++) a[i]=read(); for(int i=1;i<=m;i++){ u=read();v=read(); add(u,v); du[v]++; } for(int i=1;i<=n;i++) if(!du[i]) a[i]=0; sort(a+1,a+n+1,cmp); for(int i=1;i<=k;i++) ans+=a[i]; cout<<ans<<endl; }
子任务 4、5:
考虑DAG的情况放到普通有向图上会发生什么。
有了子任务 3 的提示,我们可以考虑把整个图缩点,将其变成一个DAG来做。
对于一个DAG,显然可以通过子任务 3 调整顺序的方式使得每个强连通分量的选择情况除选点个数以外互不影响。故下面只讨论一个强连通分量内部的情况。
一个强连通分量显然可以看作是一棵外向树加上很多边得到的。
一棵外向树的定义:一个外向树的任意一个节点要么为叶节点,要么它与孩子 间的所有边都是由它指向孩子。
一棵外向树显然是一个 DAG 。按照之前对 DAG 上情况的说明,显然我们可以 选择除了根节点以外的任意节点。
因为一个强连通分量内部是互相连通的,于是我们不妨钦定一个点为根。
对于一个没有入度的强连通分量,我们不妨钦定点权最小的点为根。这样显然 选择的是最优的。
对于一个有入度的强连通分量,我们不妨钦定那个有入度的点为根。这样在选 择到只剩根节点的时候,因为根节点有入度,所以根节点是可以被选择的。于是这 个强连通分量可以被全部选择。这显然是最优的。
这样综合上述讨论,有入度的强连通分量可以随便选,没有入度的强连通分量 去掉最小的点权的点。剩下贪心取前 k 个就可以了。
进行一次 tarjan的复杂度是 O(n+m),选前 k 个点可以排序一下。这样总复杂 度 O(m+nlogn),期望得分 35 分。注意到复杂度瓶颈在排序上,考虑我们只需要前 k 大而不需要具体前 k 个之间的大小关系,于是使用 std::nth_element()函数可 以将复杂度降至 O(n+m)。期望得分 40 分。注意,输入规模到了 10 7 级别,需要 fread 来实现读入优化。

#include <cstdio> #include <algorithm> #include <functional> #ifdef ONLINE_JUDGE #define freopen(a, b, c) #endif typedef long long int ll; namespace IPT { const int L = 1000000; char buf[L], *front=buf, *end=buf; char GetChar() { if (front == end) { end = buf + fread(front = buf, 1, L, stdin); if (front == end) return -1; } return *(front++); } } template <typename T> inline void qr(T &x) { char ch = IPT::GetChar(), lst = ' '; while ((ch > '9') || (ch < '0')) lst = ch, ch=IPT::GetChar(); while ((ch >= '0') && (ch <= '9')) x = (x << 1) + (x << 3) + (ch ^ 48), ch = IPT::GetChar(); if (lst == '-') x = -x; } const int maxn = 1000006; struct Edge { int v; Edge *nxt; Edge(const int _v, Edge *h) : v(_v), nxt(h) {} }; Edge *hd[maxn]; int n, m, k, vistime, top, scnt; int MU[maxn], dfn[maxn], low[maxn], stack[maxn], belong[maxn], minv[maxn]; bool instack[maxn], haveind[maxn]; void tarjan(const int u); int main() { freopen("zay.in", "r", stdin); freopen("zay.out", "w", stdout); qr(n); qr(m); qr(k); MU[0] = 2333; for (int i = 1; i <= n; ++i) qr(MU[i]); for (int i = 1, u, v; i <= m; ++i) { u = v = 0; qr(u); qr(v); hd[u] = new Edge(v, hd[u]); } for (int i = 1; i <= n; ++i) if (!dfn[i]) { tarjan(i); } for (int u = 1; u <= n; ++u) { for (auto e = hd[u]; e; e = e->nxt) if (belong[u] != belong[e->v]) { haveind[belong[e->v]] = true; } } for (int i = 1; i <= scnt; ++i) if (!haveind[i]) { MU[minv[i]] = 0; } std::nth_element(MU + 1, MU + 1 + k, MU + 1 + n, std::greater<int>()); int ans = 0; for (int i = 1; i <= k; ++i) { ans += MU[i]; } printf("%d\n", ans); return 0; } void tarjan(const int u) { dfn[u] = low[u] = ++vistime; instack[stack[++top] = u] = true; for (auto e = hd[u]; e; e = e->nxt) { int v = e->v; if (!dfn[v]) { tarjan(v); low[u] = std::min(low[u], low[v]); } else if (instack[v]) { low[u] = std::min(low[u], dfn[v]); } } if (dfn[u] == low[u]) { int v, &_mv = minv[++scnt]; do { instack[v = stack[top--]] = false; belong[v] = scnt; if (MU[v] < MU[_mv]) _mv = v; } while (v != u); } }
然后关于tarjan:【here】
然后关于写的很走心的题解:
然后关于TARJAN:
- 它就是一个板子
- 看YY(最后)
end-





