【细小碎的oi小知识点总结贴】不定时更新（显然也没人看qwq）

1.memcpy：

从a数组中复制k个元素到b数组：

memcpy(b,a,sizeof(int)*k);

#include<cstring>
#include<iostream>
#include<cstdio>
using namespace std;
int a[10],b[20];
int main(){
    for(int i=0;i<10;i++)
        cin>>a[i];
    for(int i=0;i<10;i++)
    cin>>b[i];
    memcpy(b,a,sizeof(int)*5);
    for(int i=0;i<20;i++)
    cout<<b[i]<<" ";
}

【输入】

1 2 3 4 5 6 7 8 9 10
10 9 8 7 6 5 4 3 2 1

【输出】

1 2 3 4 5 5 4 3 2 1 0 0 0 0 0 0 0 0 0 0 

（b数组的值被更新了，上面的话b数组的前k个值就被赋值变成了a数组的前k个值【从0开始qwq】b数组其他值不变）

将a全部赋值给b：

memcpy(b,a,sizeof(a));

#include<cstring>
#include<iostream>
#include<cstdio>
using namespace std;
int a[10],b[20];
int main(){
    for(int i=0;i<10;i++)
        cin>>a[i];
    for(int i=0;i<10;i++)
    cin>>b[i];
    memcpy(b,a,sizeof(a));
    for(int i=0;i<20;i++)
    cout<<b[i]<<" ";
}

【输入】

1 2 3 4 5 6 7 8 9 10
10 9 8 7 6 5 4 3 2 1

【输出】

1 2 3 4 5 6 7 8 9 10 0 0 0 0 0 0 0 0 0 0 

为什么突然写这个，因为用到了啊qwq（我是不会告诉你人家是题解上用的qwq）

 2.数据类的东西吧qwq：

①int范围的无穷大：INT_MAX，无穷小INT_MIN。

②memset赋值：可以正常赋值的：-1,0；神奇的赋值：（一个很大的数）0xfff（大概几个f是没问题的qwq）

 2.优先队列（priority queue）：

首先，你需要：

#include<queue>

优先队列，顾名思义，是比对列更加强大的队列。它的功能强大在它可以自动排序。

自动排序是从大到小qwq

那么如何从小到大排呢？

重载来帮忙：（作为大括号不换行的异教徒）

struct node{
    int x,y;
    bool operator < (const node & a) const{
        return x<a.x;
    }
};

声明：priority_queue<结构类型> 队列名；

常用声明格式：

priority_queue <node> q;
//node是一个结构体
//结构体里重载了‘<’小于符号
priority_queue <int,vector<int>,greater<int> > q;
//注意后面两个“>”不要写在一起，“>>”是右移运算符
//从小到大排序
priority_queue <int,vector<int>,less<int> >q;

//从大到小排序

基本操作：

 3.set

头文件#include<set>

特点：

1、set中的元素都是排好序的

2、set集合中没有重复的元素

基本操作

前向星存图（一个神奇的超越邻接矩阵的存在）

首先讲一下需要定义的一些东西？？

1.head数组：head[点数]：head[i]表示以当前点i为起点的最后一条边（这里的最后指的是编号【我们按输入顺序给边编一个号】）。

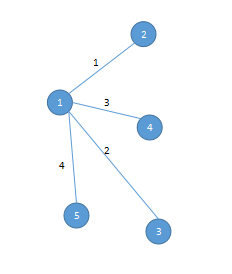
这个图即为head[1]=4，表示以1为起点的边的最后一条是点1—>点5编号为4的边；

2.num_edge，表示边的总个数；

3.结构体：

struct Edge{
    int next,to,dis;
}edge[边数];

这里，edge[i].next表示上一条以i为起点的边：：

还是上面那个图，这里edge[4].next=3；

edge[i].to表示这条边i的终点；

edge[i].dis表示这条边的权值；

void addedge(int from,int to,int dis){
    num_edge++;//因为存入一条边，总边数+1;
    edge[num_edge].next=head[from];//新存入一条以from为起点的边，之前的以from为起点的最后一条边变成了新边的上一条边
    edge[num_edge].to=to;//存终点
    edge[num_edge].dis=dis;//存权值
    head[from]=num_edge;//存入一条以from为起点的边，那么现在以from为起点的最后一条边就是新存入的边
}

提醒：如果要存的是无向图，进行程序时应该：addedge(from,to,dis)，addedge(to,from,dis)各跑一遍，所开空间也要*2；

memset的用法

memset按位赋值：一位等于8字节（一个int型是4位），（一字节可以看做是二进制中的一位），对于memset，无论你这个数是什么，它都会把每一位都变成第一位的数，如果我们用memset赋值1的话，最后结果就是这个数：

（一个蓝框为1位）

而memset（a，63,sizeof（a））；就是把a数组的初始值赋成了以下这个数：

floyd：

1. floyd实际上是一个DP（floyd：哈哈想不到吧qwq）
2. floyd其实是一个三维DP
3. floyd其实就跟01背包一样把k这一维降掉了，因此k要放在最外层枚举；
4. 对于没有降维的三维floyd dis_{k,i,j来讲，表示的是从i=>j只可能经过1——k这些点的最短路径；}

sort-cmp：

cmp函数的含义：如果返回值是 True，表示 要把 序列 (X,Y)，X放Y前。
Tarjan：

关于tarjan：【here】

slow slow read了解一下：

首先是关于数据读入的几个结点：

1. 1e4 可以用cin，没问题
2. 1e5   scanf
3. 1e6   getchar（也就是平常写的快读）
4. 1e7   fread（要背板子比较好）
5. 1e8及以上 emm，再见！

现在来写一下1e6 getchar型slow slow read：

inline int read(){
    int ans=0;
    char last=' ',ch=getchar();
    while(ch<'0'||ch>'9') last = ch,ch=getchar();//过滤空格
    while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

然后大致就是用getchar读入（大概会快吧），然后转化成数字；

然后（不知道为什么最近那么喜欢用然后qwq），粘一粘各种不同大佬喜欢用的快读板子qwq：

int read(){
    int x = 0; char c = gc();
    while(!isdigit(c)) c = gc();
    while(isdigit(c)){x = x * 10 + c - '0'; c = gc();}
    return x;
}

template <typename T>
inline void qr(T &x) {
  char ch;
  do { ch = getchar(); } while ((ch > '9') || (ch < '0'));
  do { x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar(); } while ((ch >= '0') && (ch <= '9'));
}//（艰难的没看懂）

typedef int ll;
inline void read(ll &num)
{
    bool flag = 0;
    num = 0;
    char c = getchar();
    while ((c < '0' || c > '9') && c != '-')
        c = getchar();
    if (c == '-')
    {
        flag = 1;
        c = getchar();
    }
    num = c - '0';
    c = getchar();
    while (c >= '0' && c <= '9')
        num = (num << 3) + (num << 1) + c - '0', c = getchar();
    if (flag)
        num *= -1;
}
inline void read(char &c)
{
    c = getchar();
    while (c == '\n' || c == '\r' || c == '\0' || c == ' ' || c == '\t')
        c = getchar();
}
inline void output(ll num)
{
    if (num < 0)
    {
        putchar('-');
        num = -num;
    }
    if (num >= 10)
        output(num / 10);
    putchar(num % 10 + '0');
}
inline void outln(ll num)
{
    output(num);
    puts("");
}
inline void outsp(ll num)
{
    output(num);
    putchar(' ');
}
inline void outln(string str) { puts(str.c_str()); }

然后对于zay大佬的fread，大概是只能背个板子：

typedef long long int ll;

namespace IPT {
  const int L = 1000000;
  char buf[L], *front=buf, *end=buf;
  char GetChar() {
    if (front == end) {
      end = buf + fread(front = buf, 1, L, stdin);
      if (front == end) return -1;
    }
    return *(front++);
  }
}

template <typename T>
inline void qr(T &x) {
  char ch = IPT::GetChar(), lst = ' ';
  while ((ch > '9') || (ch < '0')) lst = ch, ch=IPT::GetChar();
  while ((ch >= '0') && (ch <= '9')) x = (x << 1) + (x << 3) + (ch ^ 48), ch = IPT::GetChar();
  if (lst == '-') x = -x;
}

 状态压缩中，如何较高效的求出共有多少个1:

（参考资料：求一个数的二进制序列中1的个数（3种方法））

 比较高效的方法是x=x&（x-1），当x=0时，进行此运算的次数也就是1的个数；

int count_one3(int m){
    int count = 0;
    while (m){
        m = m&(m - 1);
        count++;
    }
    return count;
}

[背包九讲]